Tutorial Playlist
Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability.
A Comprehensive Look at Percentile in Statistics

The Best Guide to Understand Bayes Theorem
Everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, a complete guide to chi-square test, what is hypothesis testing in statistics types and examples, understanding the fundamentals of arithmetic and geometric progression, the definitive guide to understand spearman’s rank correlation, mean squared error: overview, examples, concepts and more, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution.
All You Need to Know About Bias in Statistics
A Complete Guide to Get a Grasp of Time Series Analysis
The Key Differences Between Z-Test Vs. T-Test
The Complete Guide to Understand Pearson's Correlation
A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, what is hypothesis testing in statistics types and examples.
Lesson 10 of 24 By Avijeet Biswal

Table of Contents
In today’s data-driven world, decisions are based on data all the time. Hypothesis plays a crucial role in that process, whether it may be making business decisions, in the health sector, academia, or in quality improvement. Without hypothesis & hypothesis tests, you risk drawing the wrong conclusions and making bad decisions. In this tutorial, you will look at Hypothesis Testing in Statistics.
The Ultimate Ticket to Top Data Science Job Roles
What Is Hypothesis Testing in Statistics?
Hypothesis Testing is a type of statistical analysis in which you put your assumptions about a population parameter to the test. It is used to estimate the relationship between 2 statistical variables.
Let's discuss few examples of statistical hypothesis from real-life -
- A teacher assumes that 60% of his college's students come from lower-middle-class families.
- A doctor believes that 3D (Diet, Dose, and Discipline) is 90% effective for diabetic patients.
Now that you know about hypothesis testing, look at the two types of hypothesis testing in statistics.
Hypothesis Testing Formula
Z = ( x̅ – μ0 ) / (σ /√n)
- Here, x̅ is the sample mean,
- μ0 is the population mean,
- σ is the standard deviation,
- n is the sample size.
How Hypothesis Testing Works?
An analyst performs hypothesis testing on a statistical sample to present evidence of the plausibility of the null hypothesis. Measurements and analyses are conducted on a random sample of the population to test a theory. Analysts use a random population sample to test two hypotheses: the null and alternative hypotheses.
The null hypothesis is typically an equality hypothesis between population parameters; for example, a null hypothesis may claim that the population means return equals zero. The alternate hypothesis is essentially the inverse of the null hypothesis (e.g., the population means the return is not equal to zero). As a result, they are mutually exclusive, and only one can be correct. One of the two possibilities, however, will always be correct.
Your Dream Career is Just Around The Corner!
Null Hypothesis and Alternate Hypothesis
The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.
H0 is the symbol for it, and it is pronounced H-naught.
The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.
Let's understand this with an example.
A sanitizer manufacturer claims that its product kills 95 percent of germs on average.
To put this company's claim to the test, create a null and alternate hypothesis.
H0 (Null Hypothesis): Average = 95%.
Alternative Hypothesis (H1): The average is less than 95%.
Another straightforward example to understand this concept is determining whether or not a coin is fair and balanced. The null hypothesis states that the probability of a show of heads is equal to the likelihood of a show of tails. In contrast, the alternate theory states that the probability of a show of heads and tails would be very different.
Become a Data Scientist with Hands-on Training!
Hypothesis Testing Calculation With Examples
Let's consider a hypothesis test for the average height of women in the United States. Suppose our null hypothesis is that the average height is 5'4". We gather a sample of 100 women and determine that their average height is 5'5". The standard deviation of population is 2.
To calculate the z-score, we would use the following formula:
z = ( x̅ – μ0 ) / (σ /√n)
z = (5'5" - 5'4") / (2" / √100)
z = 0.5 / (0.045)
We will reject the null hypothesis as the z-score of 11.11 is very large and conclude that there is evidence to suggest that the average height of women in the US is greater than 5'4".
Steps of Hypothesis Testing
Hypothesis testing is a statistical method to determine if there is enough evidence in a sample of data to infer that a certain condition is true for the entire population. Here’s a breakdown of the typical steps involved in hypothesis testing:
Formulate Hypotheses
- Null Hypothesis (H0): This hypothesis states that there is no effect or difference, and it is the hypothesis you attempt to reject with your test.
- Alternative Hypothesis (H1 or Ha): This hypothesis is what you might believe to be true or hope to prove true. It is usually considered the opposite of the null hypothesis.
Choose the Significance Level (α)
The significance level, often denoted by alpha (α), is the probability of rejecting the null hypothesis when it is true. Common choices for α are 0.05 (5%), 0.01 (1%), and 0.10 (10%).
Select the Appropriate Test
Choose a statistical test based on the type of data and the hypothesis. Common tests include t-tests, chi-square tests, ANOVA, and regression analysis. The selection depends on data type, distribution, sample size, and whether the hypothesis is one-tailed or two-tailed.
Collect Data
Gather the data that will be analyzed in the test. This data should be representative of the population to infer conclusions accurately.
Calculate the Test Statistic
Based on the collected data and the chosen test, calculate a test statistic that reflects how much the observed data deviates from the null hypothesis.
Determine the p-value
The p-value is the probability of observing test results at least as extreme as the results observed, assuming the null hypothesis is correct. It helps determine the strength of the evidence against the null hypothesis.
Make a Decision
Compare the p-value to the chosen significance level:
- If the p-value ≤ α: Reject the null hypothesis, suggesting sufficient evidence in the data supports the alternative hypothesis.
- If the p-value > α: Do not reject the null hypothesis, suggesting insufficient evidence to support the alternative hypothesis.
Report the Results
Present the findings from the hypothesis test, including the test statistic, p-value, and the conclusion about the hypotheses.
Perform Post-hoc Analysis (if necessary)
Depending on the results and the study design, further analysis may be needed to explore the data more deeply or to address multiple comparisons if several hypotheses were tested simultaneously.
Types of Hypothesis Testing
To determine whether a discovery or relationship is statistically significant, hypothesis testing uses a z-test. It usually checks to see if two means are the same (the null hypothesis). Only when the population standard deviation is known and the sample size is 30 data points or more, can a z-test be applied.
A statistical test called a t-test is employed to compare the means of two groups. To determine whether two groups differ or if a procedure or treatment affects the population of interest, it is frequently used in hypothesis testing.
Chi-Square
You utilize a Chi-square test for hypothesis testing concerning whether your data is as predicted. To determine if the expected and observed results are well-fitted, the Chi-square test analyzes the differences between categorical variables from a random sample. The test's fundamental premise is that the observed values in your data should be compared to the predicted values that would be present if the null hypothesis were true.
Hypothesis Testing and Confidence Intervals
Both confidence intervals and hypothesis tests are inferential techniques that depend on approximating the sample distribution. Data from a sample is used to estimate a population parameter using confidence intervals. Data from a sample is used in hypothesis testing to examine a given hypothesis. We must have a postulated parameter to conduct hypothesis testing.
Bootstrap distributions and randomization distributions are created using comparable simulation techniques. The observed sample statistic is the focal point of a bootstrap distribution, whereas the null hypothesis value is the focal point of a randomization distribution.
A variety of feasible population parameter estimates are included in confidence ranges. In this lesson, we created just two-tailed confidence intervals. There is a direct connection between these two-tail confidence intervals and these two-tail hypothesis tests. The results of a two-tailed hypothesis test and two-tailed confidence intervals typically provide the same results. In other words, a hypothesis test at the 0.05 level will virtually always fail to reject the null hypothesis if the 95% confidence interval contains the predicted value. A hypothesis test at the 0.05 level will nearly certainly reject the null hypothesis if the 95% confidence interval does not include the hypothesized parameter.
Become a Data Scientist through hands-on learning with hackathons, masterclasses, webinars, and Ask-Me-Anything! Start learning now!
Simple and Composite Hypothesis Testing
Depending on the population distribution, you can classify the statistical hypothesis into two types.
Simple Hypothesis: A simple hypothesis specifies an exact value for the parameter.
Composite Hypothesis: A composite hypothesis specifies a range of values.
A company is claiming that their average sales for this quarter are 1000 units. This is an example of a simple hypothesis.
Suppose the company claims that the sales are in the range of 900 to 1000 units. Then this is a case of a composite hypothesis.
One-Tailed and Two-Tailed Hypothesis Testing
The One-Tailed test, also called a directional test, considers a critical region of data that would result in the null hypothesis being rejected if the test sample falls into it, inevitably meaning the acceptance of the alternate hypothesis.
In a one-tailed test, the critical distribution area is one-sided, meaning the test sample is either greater or lesser than a specific value.
In two tails, the test sample is checked to be greater or less than a range of values in a Two-Tailed test, implying that the critical distribution area is two-sided.
If the sample falls within this range, the alternate hypothesis will be accepted, and the null hypothesis will be rejected.
Become a Data Scientist With Real-World Experience
Right Tailed Hypothesis Testing
If the larger than (>) sign appears in your hypothesis statement, you are using a right-tailed test, also known as an upper test. Or, to put it another way, the disparity is to the right. For instance, you can contrast the battery life before and after a change in production. Your hypothesis statements can be the following if you want to know if the battery life is longer than the original (let's say 90 hours):
- The null hypothesis is (H0 <= 90) or less change.
- A possibility is that battery life has risen (H1) > 90.
The crucial point in this situation is that the alternate hypothesis (H1), not the null hypothesis, decides whether you get a right-tailed test.
Left Tailed Hypothesis Testing
Alternative hypotheses that assert the true value of a parameter is lower than the null hypothesis are tested with a left-tailed test; they are indicated by the asterisk "<".
Suppose H0: mean = 50 and H1: mean not equal to 50
According to the H1, the mean can be greater than or less than 50. This is an example of a Two-tailed test.
In a similar manner, if H0: mean >=50, then H1: mean <50
Here the mean is less than 50. It is called a One-tailed test.
Type 1 and Type 2 Error
A hypothesis test can result in two types of errors.
Type 1 Error: A Type-I error occurs when sample results reject the null hypothesis despite being true.
Type 2 Error: A Type-II error occurs when the null hypothesis is not rejected when it is false, unlike a Type-I error.
Suppose a teacher evaluates the examination paper to decide whether a student passes or fails.
H0: Student has passed
H1: Student has failed
Type I error will be the teacher failing the student [rejects H0] although the student scored the passing marks [H0 was true].
Type II error will be the case where the teacher passes the student [do not reject H0] although the student did not score the passing marks [H1 is true].
Level of Significance
The alpha value is a criterion for determining whether a test statistic is statistically significant. In a statistical test, Alpha represents an acceptable probability of a Type I error. Because alpha is a probability, it can be anywhere between 0 and 1. In practice, the most commonly used alpha values are 0.01, 0.05, and 0.1, which represent a 1%, 5%, and 10% chance of a Type I error, respectively (i.e. rejecting the null hypothesis when it is in fact correct).
A p-value is a metric that expresses the likelihood that an observed difference could have occurred by chance. As the p-value decreases the statistical significance of the observed difference increases. If the p-value is too low, you reject the null hypothesis.
Here you have taken an example in which you are trying to test whether the new advertising campaign has increased the product's sales. The p-value is the likelihood that the null hypothesis, which states that there is no change in the sales due to the new advertising campaign, is true. If the p-value is .30, then there is a 30% chance that there is no increase or decrease in the product's sales. If the p-value is 0.03, then there is a 3% probability that there is no increase or decrease in the sales value due to the new advertising campaign. As you can see, the lower the p-value, the chances of the alternate hypothesis being true increases, which means that the new advertising campaign causes an increase or decrease in sales.
Our Data Scientist Master's Program covers core topics such as R, Python, Machine Learning, Tableau, Hadoop, and Spark. Get started on your journey today!
Why Is Hypothesis Testing Important in Research Methodology?
Hypothesis testing is crucial in research methodology for several reasons:
- Provides evidence-based conclusions: It allows researchers to make objective conclusions based on empirical data, providing evidence to support or refute their research hypotheses.
- Supports decision-making: It helps make informed decisions, such as accepting or rejecting a new treatment, implementing policy changes, or adopting new practices.
- Adds rigor and validity: It adds scientific rigor to research using statistical methods to analyze data, ensuring that conclusions are based on sound statistical evidence.
- Contributes to the advancement of knowledge: By testing hypotheses, researchers contribute to the growth of knowledge in their respective fields by confirming existing theories or discovering new patterns and relationships.
When Did Hypothesis Testing Begin?
Hypothesis testing as a formalized process began in the early 20th century, primarily through the work of statisticians such as Ronald A. Fisher, Jerzy Neyman, and Egon Pearson. The development of hypothesis testing is closely tied to the evolution of statistical methods during this period.
- Ronald A. Fisher (1920s): Fisher was one of the key figures in developing the foundation for modern statistical science. In the 1920s, he introduced the concept of the null hypothesis in his book "Statistical Methods for Research Workers" (1925). Fisher also developed significance testing to examine the likelihood of observing the collected data if the null hypothesis were true. He introduced p-values to determine the significance of the observed results.
- Neyman-Pearson Framework (1930s): Jerzy Neyman and Egon Pearson built on Fisher’s work and formalized the process of hypothesis testing even further. In the 1930s, they introduced the concepts of Type I and Type II errors and developed a decision-making framework widely used in hypothesis testing today. Their approach emphasized the balance between these errors and introduced the concepts of the power of a test and the alternative hypothesis.
The dialogue between Fisher's and Neyman-Pearson's approaches shaped the methods and philosophy of statistical hypothesis testing used today. Fisher emphasized the evidential interpretation of the p-value. At the same time, Neyman and Pearson advocated for a decision-theoretical approach in which hypotheses are either accepted or rejected based on pre-determined significance levels and power considerations.
The application and methodology of hypothesis testing have since become a cornerstone of statistical analysis across various scientific disciplines, marking a significant statistical development.
Limitations of Hypothesis Testing
Hypothesis testing has some limitations that researchers should be aware of:
- It cannot prove or establish the truth: Hypothesis testing provides evidence to support or reject a hypothesis, but it cannot confirm the absolute truth of the research question.
- Results are sample-specific: Hypothesis testing is based on analyzing a sample from a population, and the conclusions drawn are specific to that particular sample.
- Possible errors: During hypothesis testing, there is a chance of committing type I error (rejecting a true null hypothesis) or type II error (failing to reject a false null hypothesis).
- Assumptions and requirements: Different tests have specific assumptions and requirements that must be met to accurately interpret results.
Learn All The Tricks Of The BI Trade
After reading this tutorial, you would have a much better understanding of hypothesis testing, one of the most important concepts in the field of Data Science . The majority of hypotheses are based on speculation about observed behavior, natural phenomena, or established theories.
If you are interested in statistics of data science and skills needed for such a career, you ought to explore the Post Graduate Program in Data Science.
If you have any questions regarding this ‘Hypothesis Testing In Statistics’ tutorial, do share them in the comment section. Our subject matter expert will respond to your queries. Happy learning!
1. What is hypothesis testing in statistics with example?
Hypothesis testing is a statistical method used to determine if there is enough evidence in a sample data to draw conclusions about a population. It involves formulating two competing hypotheses, the null hypothesis (H0) and the alternative hypothesis (Ha), and then collecting data to assess the evidence. An example: testing if a new drug improves patient recovery (Ha) compared to the standard treatment (H0) based on collected patient data.
2. What is H0 and H1 in statistics?
In statistics, H0 and H1 represent the null and alternative hypotheses. The null hypothesis, H0, is the default assumption that no effect or difference exists between groups or conditions. The alternative hypothesis, H1, is the competing claim suggesting an effect or a difference. Statistical tests determine whether to reject the null hypothesis in favor of the alternative hypothesis based on the data.
3. What is a simple hypothesis with an example?
A simple hypothesis is a specific statement predicting a single relationship between two variables. It posits a direct and uncomplicated outcome. For example, a simple hypothesis might state, "Increased sunlight exposure increases the growth rate of sunflowers." Here, the hypothesis suggests a direct relationship between the amount of sunlight (independent variable) and the growth rate of sunflowers (dependent variable), with no additional variables considered.
4. What are the 2 types of hypothesis testing?
- One-tailed (or one-sided) test: Tests for the significance of an effect in only one direction, either positive or negative.
- Two-tailed (or two-sided) test: Tests for the significance of an effect in both directions, allowing for the possibility of a positive or negative effect.
The choice between one-tailed and two-tailed tests depends on the specific research question and the directionality of the expected effect.
5. What are the 3 major types of hypothesis?
The three major types of hypotheses are:
- Null Hypothesis (H0): Represents the default assumption, stating that there is no significant effect or relationship in the data.
- Alternative Hypothesis (Ha): Contradicts the null hypothesis and proposes a specific effect or relationship that researchers want to investigate.
- Nondirectional Hypothesis: An alternative hypothesis that doesn't specify the direction of the effect, leaving it open for both positive and negative possibilities.
Find our PL-300 Microsoft Power BI Certification Training Online Classroom training classes in top cities:
| Name | Date | Place | |
|---|---|---|---|
| 24 Aug -8 Sep 2024, Weekend batch | Your City | ||
| 7 Sep -22 Sep 2024, Weekend batch | Your City | ||
| 21 Sep -6 Oct 2024, Weekend batch | Your City |
About the Author
Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.
Recommended Resources
Free eBook: Top Programming Languages For A Data Scientist
Normality Test in Minitab: Minitab with Statistics
Machine Learning Career Guide: A Playbook to Becoming a Machine Learning Engineer
- PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.
- Search Search Please fill out this field.
What Is Hypothesis Testing?
- How It Works
4 Step Process
The bottom line.
- Fundamental Analysis
Hypothesis Testing: 4 Steps and Example
:max_bytes(150000):strip_icc():format(webp)/ChristinaMajaski-5c9433ea46e0fb0001d880b1.jpeg)
Hypothesis testing, sometimes called significance testing, is an act in statistics whereby an analyst tests an assumption regarding a population parameter. The methodology employed by the analyst depends on the nature of the data used and the reason for the analysis.
Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data. Such data may come from a larger population or a data-generating process. The word "population" will be used for both of these cases in the following descriptions.
Key Takeaways
- Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data.
- The test provides evidence concerning the plausibility of the hypothesis, given the data.
- Statistical analysts test a hypothesis by measuring and examining a random sample of the population being analyzed.
- The four steps of hypothesis testing include stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.
How Hypothesis Testing Works
In hypothesis testing, an analyst tests a statistical sample, intending to provide evidence on the plausibility of the null hypothesis. Statistical analysts measure and examine a random sample of the population being analyzed. All analysts use a random population sample to test two different hypotheses: the null hypothesis and the alternative hypothesis.
The null hypothesis is usually a hypothesis of equality between population parameters; e.g., a null hypothesis may state that the population mean return is equal to zero. The alternative hypothesis is effectively the opposite of a null hypothesis. Thus, they are mutually exclusive , and only one can be true. However, one of the two hypotheses will always be true.
The null hypothesis is a statement about a population parameter, such as the population mean, that is assumed to be true.
- State the hypotheses.
- Formulate an analysis plan, which outlines how the data will be evaluated.
- Carry out the plan and analyze the sample data.
- Analyze the results and either reject the null hypothesis, or state that the null hypothesis is plausible, given the data.
Example of Hypothesis Testing
If an individual wants to test that a penny has exactly a 50% chance of landing on heads, the null hypothesis would be that 50% is correct, and the alternative hypothesis would be that 50% is not correct. Mathematically, the null hypothesis is represented as Ho: P = 0.5. The alternative hypothesis is shown as "Ha" and is identical to the null hypothesis, except with the equal sign struck-through, meaning that it does not equal 50%.
A random sample of 100 coin flips is taken, and the null hypothesis is tested. If it is found that the 100 coin flips were distributed as 40 heads and 60 tails, the analyst would assume that a penny does not have a 50% chance of landing on heads and would reject the null hypothesis and accept the alternative hypothesis.
If there were 48 heads and 52 tails, then it is plausible that the coin could be fair and still produce such a result. In cases such as this where the null hypothesis is "accepted," the analyst states that the difference between the expected results (50 heads and 50 tails) and the observed results (48 heads and 52 tails) is "explainable by chance alone."
When Did Hypothesis Testing Begin?
Some statisticians attribute the first hypothesis tests to satirical writer John Arbuthnot in 1710, who studied male and female births in England after observing that in nearly every year, male births exceeded female births by a slight proportion. Arbuthnot calculated that the probability of this happening by chance was small, and therefore it was due to “divine providence.”
What are the Benefits of Hypothesis Testing?
Hypothesis testing helps assess the accuracy of new ideas or theories by testing them against data. This allows researchers to determine whether the evidence supports their hypothesis, helping to avoid false claims and conclusions. Hypothesis testing also provides a framework for decision-making based on data rather than personal opinions or biases. By relying on statistical analysis, hypothesis testing helps to reduce the effects of chance and confounding variables, providing a robust framework for making informed conclusions.
What are the Limitations of Hypothesis Testing?
Hypothesis testing relies exclusively on data and doesn’t provide a comprehensive understanding of the subject being studied. Additionally, the accuracy of the results depends on the quality of the available data and the statistical methods used. Inaccurate data or inappropriate hypothesis formulation may lead to incorrect conclusions or failed tests. Hypothesis testing can also lead to errors, such as analysts either accepting or rejecting a null hypothesis when they shouldn’t have. These errors may result in false conclusions or missed opportunities to identify significant patterns or relationships in the data.
Hypothesis testing refers to a statistical process that helps researchers determine the reliability of a study. By using a well-formulated hypothesis and set of statistical tests, individuals or businesses can make inferences about the population that they are studying and draw conclusions based on the data presented. All hypothesis testing methods have the same four-step process, which includes stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.
Sage. " Introduction to Hypothesis Testing ," Page 4.
Elder Research. " Who Invented the Null Hypothesis? "
Formplus. " Hypothesis Testing: Definition, Uses, Limitations and Examples ."
:max_bytes(150000):strip_icc():format(webp)/null_hypothesis-finalE-56a4132b022f49f0a3d469c6882ddd99.jpg)
- Terms of Service
- Editorial Policy
- Privacy Policy
Reset password New user? Sign up
Existing user? Log in
Hypothesis Testing
Already have an account? Log in here.
A hypothesis test is a statistical inference method used to test the significance of a proposed (hypothesized) relation between population statistics (parameters) and their corresponding sample estimators . In other words, hypothesis tests are used to determine if there is enough evidence in a sample to prove a hypothesis true for the entire population.
The test considers two hypotheses: the null hypothesis , which is a statement meant to be tested, usually something like "there is no effect" with the intention of proving this false, and the alternate hypothesis , which is the statement meant to stand after the test is performed. The two hypotheses must be mutually exclusive ; moreover, in most applications, the two are complementary (one being the negation of the other). The test works by comparing the \(p\)-value to the level of significance (a chosen target). If the \(p\)-value is less than or equal to the level of significance, then the null hypothesis is rejected.
When analyzing data, only samples of a certain size might be manageable as efficient computations. In some situations the error terms follow a continuous or infinite distribution, hence the use of samples to suggest accuracy of the chosen test statistics. The method of hypothesis testing gives an advantage over guessing what distribution or which parameters the data follows.
Definitions and Methodology
Hypothesis test and confidence intervals.
In statistical inference, properties (parameters) of a population are analyzed by sampling data sets. Given assumptions on the distribution, i.e. a statistical model of the data, certain hypotheses can be deduced from the known behavior of the model. These hypotheses must be tested against sampled data from the population.
The null hypothesis \((\)denoted \(H_0)\) is a statement that is assumed to be true. If the null hypothesis is rejected, then there is enough evidence (statistical significance) to accept the alternate hypothesis \((\)denoted \(H_1).\) Before doing any test for significance, both hypotheses must be clearly stated and non-conflictive, i.e. mutually exclusive, statements. Rejecting the null hypothesis, given that it is true, is called a type I error and it is denoted \(\alpha\), which is also its probability of occurrence. Failing to reject the null hypothesis, given that it is false, is called a type II error and it is denoted \(\beta\), which is also its probability of occurrence. Also, \(\alpha\) is known as the significance level , and \(1-\beta\) is known as the power of the test. \(H_0\) \(\textbf{is true}\)\(\hspace{15mm}\) \(H_0\) \(\textbf{is false}\) \(\textbf{Reject}\) \(H_0\)\(\hspace{10mm}\) Type I error Correct Decision \(\textbf{Reject}\) \(H_1\) Correct Decision Type II error The test statistic is the standardized value following the sampled data under the assumption that the null hypothesis is true, and a chosen particular test. These tests depend on the statistic to be studied and the assumed distribution it follows, e.g. the population mean following a normal distribution. The \(p\)-value is the probability of observing an extreme test statistic in the direction of the alternate hypothesis, given that the null hypothesis is true. The critical value is the value of the assumed distribution of the test statistic such that the probability of making a type I error is small.
Methodologies: Given an estimator \(\hat \theta\) of a population statistic \(\theta\), following a probability distribution \(P(T)\), computed from a sample \(\mathcal{S},\) and given a significance level \(\alpha\) and test statistic \(t^*,\) define \(H_0\) and \(H_1;\) compute the test statistic \(t^*.\) \(p\)-value Approach (most prevalent): Find the \(p\)-value using \(t^*\) (right-tailed). If the \(p\)-value is at most \(\alpha,\) reject \(H_0\). Otherwise, reject \(H_1\). Critical Value Approach: Find the critical value solving the equation \(P(T\geq t_\alpha)=\alpha\) (right-tailed). If \(t^*>t_\alpha\), reject \(H_0\). Otherwise, reject \(H_1\). Note: Failing to reject \(H_0\) only means inability to accept \(H_1\), and it does not mean to accept \(H_0\).
Assume a normally distributed population has recorded cholesterol levels with various statistics computed. From a sample of 100 subjects in the population, the sample mean was 214.12 mg/dL (milligrams per deciliter), with a sample standard deviation of 45.71 mg/dL. Perform a hypothesis test, with significance level 0.05, to test if there is enough evidence to conclude that the population mean is larger than 200 mg/dL. Hypothesis Test We will perform a hypothesis test using the \(p\)-value approach with significance level \(\alpha=0.05:\) Define \(H_0\): \(\mu=200\). Define \(H_1\): \(\mu>200\). Since our values are normally distributed, the test statistic is \(z^*=\frac{\bar X - \mu_0}{\frac{s}{\sqrt{n}}}=\frac{214.12 - 200}{\frac{45.71}{\sqrt{100}}}\approx 3.09\). Using a standard normal distribution, we find that our \(p\)-value is approximately \(0.001\). Since the \(p\)-value is at most \(\alpha=0.05,\) we reject \(H_0\). Therefore, we can conclude that the test shows sufficient evidence to support the claim that \(\mu\) is larger than \(200\) mg/dL.
If the sample size was smaller, the normal and \(t\)-distributions behave differently. Also, the question itself must be managed by a double-tail test instead.
Assume a population's cholesterol levels are recorded and various statistics are computed. From a sample of 25 subjects, the sample mean was 214.12 mg/dL (milligrams per deciliter), with a sample standard deviation of 45.71 mg/dL. Perform a hypothesis test, with significance level 0.05, to test if there is enough evidence to conclude that the population mean is not equal to 200 mg/dL. Hypothesis Test We will perform a hypothesis test using the \(p\)-value approach with significance level \(\alpha=0.05\) and the \(t\)-distribution with 24 degrees of freedom: Define \(H_0\): \(\mu=200\). Define \(H_1\): \(\mu\neq 200\). Using the \(t\)-distribution, the test statistic is \(t^*=\frac{\bar X - \mu_0}{\frac{s}{\sqrt{n}}}=\frac{214.12 - 200}{\frac{45.71}{\sqrt{25}}}\approx 1.54\). Using a \(t\)-distribution with 24 degrees of freedom, we find that our \(p\)-value is approximately \(2(0.068)=0.136\). We have multiplied by two since this is a two-tailed argument, i.e. the mean can be smaller than or larger than. Since the \(p\)-value is larger than \(\alpha=0.05,\) we fail to reject \(H_0\). Therefore, the test does not show sufficient evidence to support the claim that \(\mu\) is not equal to \(200\) mg/dL.
The complement of the rejection on a two-tailed hypothesis test (with significance level \(\alpha\)) for a population parameter \(\theta\) is equivalent to finding a confidence interval \((\)with confidence level \(1-\alpha)\) for the population parameter \(\theta\). If the assumption on the parameter \(\theta\) falls inside the confidence interval, then the test has failed to reject the null hypothesis \((\)with \(p\)-value greater than \(\alpha).\) Otherwise, if \(\theta\) does not fall in the confidence interval, then the null hypothesis is rejected in favor of the alternate \((\)with \(p\)-value at most \(\alpha).\)
- Statistics (Estimation)
- Normal Distribution
- Correlation
- Confidence Intervals
Problem Loading...
Note Loading...
Set Loading...
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Unit 12: Significance tests (hypothesis testing)
About this unit.
Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values to make conclusions about hypotheses.
The idea of significance tests
- Simple hypothesis testing (Opens a modal)
- Idea behind hypothesis testing (Opens a modal)
- Examples of null and alternative hypotheses (Opens a modal)
- P-values and significance tests (Opens a modal)
- Comparing P-values to different significance levels (Opens a modal)
- Estimating a P-value from a simulation (Opens a modal)
- Using P-values to make conclusions (Opens a modal)
- Simple hypothesis testing Get 3 of 4 questions to level up!
- Writing null and alternative hypotheses Get 3 of 4 questions to level up!
- Estimating P-values from simulations Get 3 of 4 questions to level up!
Error probabilities and power
- Introduction to Type I and Type II errors (Opens a modal)
- Type 1 errors (Opens a modal)
- Examples identifying Type I and Type II errors (Opens a modal)
- Introduction to power in significance tests (Opens a modal)
- Examples thinking about power in significance tests (Opens a modal)
- Consequences of errors and significance (Opens a modal)
- Type I vs Type II error Get 3 of 4 questions to level up!
- Error probabilities and power Get 3 of 4 questions to level up!
Tests about a population proportion
- Constructing hypotheses for a significance test about a proportion (Opens a modal)
- Conditions for a z test about a proportion (Opens a modal)
- Reference: Conditions for inference on a proportion (Opens a modal)
- Calculating a z statistic in a test about a proportion (Opens a modal)
- Calculating a P-value given a z statistic (Opens a modal)
- Making conclusions in a test about a proportion (Opens a modal)
- Writing hypotheses for a test about a proportion Get 3 of 4 questions to level up!
- Conditions for a z test about a proportion Get 3 of 4 questions to level up!
- Calculating the test statistic in a z test for a proportion Get 3 of 4 questions to level up!
- Calculating the P-value in a z test for a proportion Get 3 of 4 questions to level up!
- Making conclusions in a z test for a proportion Get 3 of 4 questions to level up!
Tests about a population mean
- Writing hypotheses for a significance test about a mean (Opens a modal)
- Conditions for a t test about a mean (Opens a modal)
- Reference: Conditions for inference on a mean (Opens a modal)
- When to use z or t statistics in significance tests (Opens a modal)
- Example calculating t statistic for a test about a mean (Opens a modal)
- Using TI calculator for P-value from t statistic (Opens a modal)
- Using a table to estimate P-value from t statistic (Opens a modal)
- Comparing P-value from t statistic to significance level (Opens a modal)
- Free response example: Significance test for a mean (Opens a modal)
- Writing hypotheses for a test about a mean Get 3 of 4 questions to level up!
- Conditions for a t test about a mean Get 3 of 4 questions to level up!
- Calculating the test statistic in a t test for a mean Get 3 of 4 questions to level up!
- Calculating the P-value in a t test for a mean Get 3 of 4 questions to level up!
- Making conclusions in a t test for a mean Get 3 of 4 questions to level up!
More significance testing videos
- Hypothesis testing and p-values (Opens a modal)
- One-tailed and two-tailed tests (Opens a modal)
- Z-statistics vs. T-statistics (Opens a modal)
- Small sample hypothesis test (Opens a modal)
- Large sample proportion hypothesis testing (Opens a modal)
Statistics Tutorial
Descriptive statistics, inferential statistics, stat reference, statistics - hypothesis testing.
Hypothesis testing is a formal way of checking if a hypothesis about a population is true or not.
Hypothesis Testing
A hypothesis is a claim about a population parameter .
A hypothesis test is a formal procedure to check if a hypothesis is true or not.
Examples of claims that can be checked:
The average height of people in Denmark is more than 170 cm.
The share of left handed people in Australia is not 10%.
The average income of dentists is less the average income of lawyers.
The Null and Alternative Hypothesis
Hypothesis testing is based on making two different claims about a population parameter.
The null hypothesis (\(H_{0} \)) and the alternative hypothesis (\(H_{1}\)) are the claims.
The two claims needs to be mutually exclusive , meaning only one of them can be true.
The alternative hypothesis is typically what we are trying to prove.
For example, we want to check the following claim:
"The average height of people in Denmark is more than 170 cm."
In this case, the parameter is the average height of people in Denmark (\(\mu\)).
The null and alternative hypothesis would be:
Null hypothesis : The average height of people in Denmark is 170 cm.
Alternative hypothesis : The average height of people in Denmark is more than 170 cm.
The claims are often expressed with symbols like this:
\(H_{0}\): \(\mu = 170 \: cm \)
\(H_{1}\): \(\mu > 170 \: cm \)
If the data supports the alternative hypothesis, we reject the null hypothesis and accept the alternative hypothesis.
If the data does not support the alternative hypothesis, we keep the null hypothesis.
Note: The alternative hypothesis is also referred to as (\(H_{A} \)).
The Significance Level
The significance level (\(\alpha\)) is the uncertainty we accept when rejecting the null hypothesis in the hypothesis test.
The significance level is a percentage probability of accidentally making the wrong conclusion.
Typical significance levels are:
- \(\alpha = 0.1\) (10%)
- \(\alpha = 0.05\) (5%)
- \(\alpha = 0.01\) (1%)
A lower significance level means that the evidence in the data needs to be stronger to reject the null hypothesis.
There is no "correct" significance level - it only states the uncertainty of the conclusion.
Note: A 5% significance level means that when we reject a null hypothesis:
We expect to reject a true null hypothesis 5 out of 100 times.
Advertisement
The Test Statistic
The test statistic is used to decide the outcome of the hypothesis test.
The test statistic is a standardized value calculated from the sample.
Standardization means converting a statistic to a well known probability distribution .
The type of probability distribution depends on the type of test.
Common examples are:
- Standard Normal Distribution (Z): used for Testing Population Proportions
- Student's T-Distribution (T): used for Testing Population Means
Note: You will learn how to calculate the test statistic for each type of test in the following chapters.
The Critical Value and P-Value Approach
There are two main approaches used for hypothesis tests:
- The critical value approach compares the test statistic with the critical value of the significance level.
- The p-value approach compares the p-value of the test statistic and with the significance level.
The Critical Value Approach
The critical value approach checks if the test statistic is in the rejection region .
The rejection region is an area of probability in the tails of the distribution.
The size of the rejection region is decided by the significance level (\(\alpha\)).
The value that separates the rejection region from the rest is called the critical value .
Here is a graphical illustration:
If the test statistic is inside this rejection region, the null hypothesis is rejected .
For example, if the test statistic is 2.3 and the critical value is 2 for a significance level (\(\alpha = 0.05\)):
We reject the null hypothesis (\(H_{0} \)) at 0.05 significance level (\(\alpha\))
The P-Value Approach
The p-value approach checks if the p-value of the test statistic is smaller than the significance level (\(\alpha\)).
The p-value of the test statistic is the area of probability in the tails of the distribution from the value of the test statistic.
If the p-value is smaller than the significance level, the null hypothesis is rejected .
The p-value directly tells us the lowest significance level where we can reject the null hypothesis.
For example, if the p-value is 0.03:
We reject the null hypothesis (\(H_{0} \)) at a 0.05 significance level (\(\alpha\))
We keep the null hypothesis (\(H_{0}\)) at a 0.01 significance level (\(\alpha\))
Note: The two approaches are only different in how they present the conclusion.
Steps for a Hypothesis Test
The following steps are used for a hypothesis test:
- Check the conditions
- Define the claims
- Decide the significance level
- Calculate the test statistic
One condition is that the sample is randomly selected from the population.
The other conditions depends on what type of parameter you are testing the hypothesis for.
Common parameters to test hypotheses are:
- Proportions (for qualitative data)
- Mean values (for numerical data)
You will learn the steps for both types in the following pages.

COLOR PICKER

Contact Sales
If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]
Report Error
If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]
Top Tutorials
Top references, top examples, get certified.
Hypothesis Testing
Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.
A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. | |
| 7. | |
| 8. |
What is Hypothesis Testing in Statistics?
Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.
Hypothesis Testing Definition
Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.
Null Hypothesis
The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as \(H_{0}\). Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.
Alternative Hypothesis
The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as \(H_{1}\) or \(H_{a}\). For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.
Hypothesis Testing P Value
In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, \(\alpha\) or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.
Hypothesis Testing Critical region
All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.
Hypothesis Testing Formula
Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:
- z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the size of the sample.
- t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). s is the sample standard deviation.
- \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\). \(O_{i}\) is the observed value and \(E_{i}\) is the expected value.
We will learn more about these test statistics in the upcoming section.
Types of Hypothesis Testing
Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.
Hypothesis Testing Z Test
A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:
- One sample: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
- Two samples: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).
Hypothesis Testing t Test
The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.
- One sample: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\).
- Two samples: t = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).
Hypothesis Testing Chi Square
The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.
One Tailed Hypothesis Testing
One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.
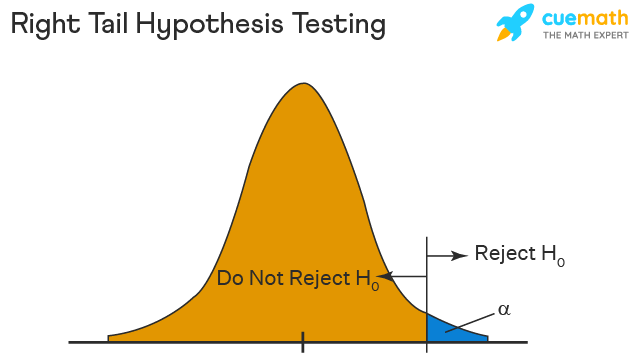
Right Tailed Hypothesis Testing
The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:
\(H_{0}\): The population parameter is ≤ some value
\(H_{1}\): The population parameter is > some value.
If the test statistic has a greater value than the critical value then the null hypothesis is rejected
Left Tailed Hypothesis Testing
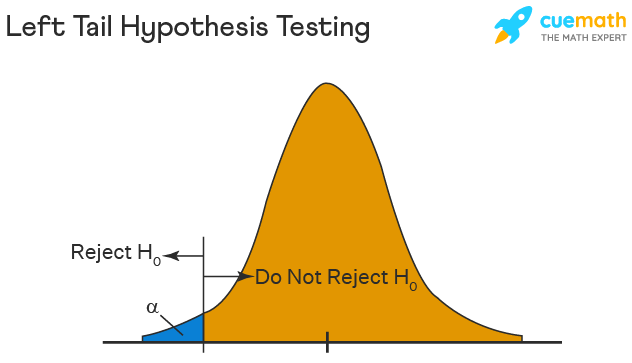
The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:
\(H_{0}\): The population parameter is ≥ some value
\(H_{1}\): The population parameter is < some value.
The null hypothesis is rejected if the test statistic has a value lesser than the critical value.
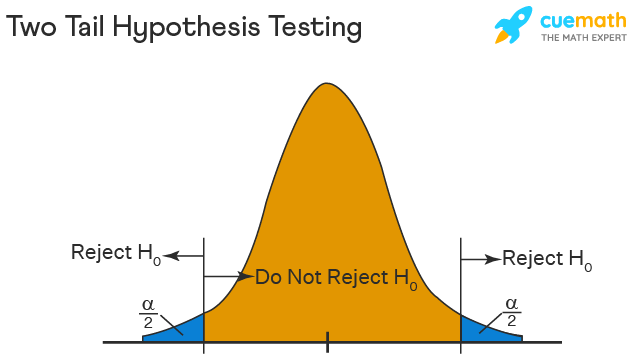
Two Tailed Hypothesis Testing
In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:
\(H_{0}\): the population parameter = some value
\(H_{1}\): the population parameter ≠ some value
The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.
Hypothesis Testing Steps
Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:
- Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
- Step 2: Set up the alternative hypothesis.
- Step 3: Choose the correct significance level, \(\alpha\), and find the critical value.
- Step 4: Calculate the correct test statistic (z, t or \(\chi\)) and p-value.
- Step 5: Compare the test statistic with the critical value or compare the p-value with \(\alpha\) to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.
Hypothesis Testing Example
The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.
Step 1: This is an example of a right-tailed test. Set up the null hypothesis as \(H_{0}\): \(\mu\) = 100.
Step 2: The alternative hypothesis is given by \(H_{1}\): \(\mu\) > 100.
Step 3: As this is a one-tailed test, \(\alpha\) = 100% - 95% = 5%. This can be used to determine the critical value.
1 - \(\alpha\) = 1 - 0.05 = 0.95
0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.
Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.
z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
\(\mu\) = 100, \(\overline{x}\) = 112.5, n = 30, \(\sigma\) = 15
z = \(\frac{112.5-100}{\frac{15}{\sqrt{30}}}\) = 4.56
Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.
Hypothesis Testing and Confidence Intervals
Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.
Related Articles:
- Probability and Statistics
- Data Handling
Important Notes on Hypothesis Testing
- Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
- It involves the setting up of a null hypothesis and an alternate hypothesis.
- There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
- Hypothesis testing can be classified as right tail, left tail, and two tail tests.
Examples on Hypothesis Testing
- Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) > 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 5, s = 18. \(\alpha\) = 0.05 Using the t-distribution table, the critical value is 2.132 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
- Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. \(H_{0}\): \(\mu\) = 80, \(H_{1}\): \(\mu\) ≠ 80 \(\overline{x}\) = 88, \(\mu\) = 80, n = 36, \(\sigma\) = 10. \(\alpha\) = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) z = \(\frac{88-80}{\frac{10}{\sqrt{36}}}\) = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
- Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) < 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = \(\frac{82-90}{\frac{18}{\sqrt{6}}}\) t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.
go to slide go to slide go to slide

Book a Free Trial Class
FAQs on Hypothesis Testing
What is hypothesis testing.
Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.
What is the z Test in Hypothesis Testing?
The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.
What is the t Test in Hypothesis Testing?
The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?
The formula for a one sample z test in hypothesis testing is z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) and for two samples is z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).
What is the p Value in Hypothesis Testing?
The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.
What is One Tail Hypothesis Testing?
When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.
What is the Alpha Level in Two Tail Hypothesis Testing?
To get the alpha level in a two tail hypothesis testing divide \(\alpha\) by 2. This is done as there are two rejection regions in the curve.
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- Indian J Crit Care Med
- v.23(Suppl 3); 2019 Sep
An Introduction to Statistics: Understanding Hypothesis Testing and Statistical Errors
Priya ranganathan.
1 Department of Anesthesiology, Critical Care and Pain, Tata Memorial Hospital, Mumbai, Maharashtra, India
2 Department of Surgical Oncology, Tata Memorial Centre, Mumbai, Maharashtra, India
The second article in this series on biostatistics covers the concepts of sample, population, research hypotheses and statistical errors.
How to cite this article
Ranganathan P, Pramesh CS. An Introduction to Statistics: Understanding Hypothesis Testing and Statistical Errors. Indian J Crit Care Med 2019;23(Suppl 3):S230–S231.
Two papers quoted in this issue of the Indian Journal of Critical Care Medicine report. The results of studies aim to prove that a new intervention is better than (superior to) an existing treatment. In the ABLE study, the investigators wanted to show that transfusion of fresh red blood cells would be superior to standard-issue red cells in reducing 90-day mortality in ICU patients. 1 The PROPPR study was designed to prove that transfusion of a lower ratio of plasma and platelets to red cells would be superior to a higher ratio in decreasing 24-hour and 30-day mortality in critically ill patients. 2 These studies are known as superiority studies (as opposed to noninferiority or equivalence studies which will be discussed in a subsequent article).
SAMPLE VERSUS POPULATION
A sample represents a group of participants selected from the entire population. Since studies cannot be carried out on entire populations, researchers choose samples, which are representative of the population. This is similar to walking into a grocery store and examining a few grains of rice or wheat before purchasing an entire bag; we assume that the few grains that we select (the sample) are representative of the entire sack of grains (the population).
The results of the study are then extrapolated to generate inferences about the population. We do this using a process known as hypothesis testing. This means that the results of the study may not always be identical to the results we would expect to find in the population; i.e., there is the possibility that the study results may be erroneous.
HYPOTHESIS TESTING
A clinical trial begins with an assumption or belief, and then proceeds to either prove or disprove this assumption. In statistical terms, this belief or assumption is known as a hypothesis. Counterintuitively, what the researcher believes in (or is trying to prove) is called the “alternate” hypothesis, and the opposite is called the “null” hypothesis; every study has a null hypothesis and an alternate hypothesis. For superiority studies, the alternate hypothesis states that one treatment (usually the new or experimental treatment) is superior to the other; the null hypothesis states that there is no difference between the treatments (the treatments are equal). For example, in the ABLE study, we start by stating the null hypothesis—there is no difference in mortality between groups receiving fresh RBCs and standard-issue RBCs. We then state the alternate hypothesis—There is a difference between groups receiving fresh RBCs and standard-issue RBCs. It is important to note that we have stated that the groups are different, without specifying which group will be better than the other. This is known as a two-tailed hypothesis and it allows us to test for superiority on either side (using a two-sided test). This is because, when we start a study, we are not 100% certain that the new treatment can only be better than the standard treatment—it could be worse, and if it is so, the study should pick it up as well. One tailed hypothesis and one-sided statistical testing is done for non-inferiority studies, which will be discussed in a subsequent paper in this series.
STATISTICAL ERRORS
There are two possibilities to consider when interpreting the results of a superiority study. The first possibility is that there is truly no difference between the treatments but the study finds that they are different. This is called a Type-1 error or false-positive error or alpha error. This means falsely rejecting the null hypothesis.
The second possibility is that there is a difference between the treatments and the study does not pick up this difference. This is called a Type 2 error or false-negative error or beta error. This means falsely accepting the null hypothesis.
The power of the study is the ability to detect a difference between groups and is the converse of the beta error; i.e., power = 1-beta error. Alpha and beta errors are finalized when the protocol is written and form the basis for sample size calculation for the study. In an ideal world, we would not like any error in the results of our study; however, we would need to do the study in the entire population (infinite sample size) to be able to get a 0% alpha and beta error. These two errors enable us to do studies with realistic sample sizes, with the compromise that there is a small possibility that the results may not always reflect the truth. The basis for this will be discussed in a subsequent paper in this series dealing with sample size calculation.
Conventionally, type 1 or alpha error is set at 5%. This means, that at the end of the study, if there is a difference between groups, we want to be 95% certain that this is a true difference and allow only a 5% probability that this difference has occurred by chance (false positive). Type 2 or beta error is usually set between 10% and 20%; therefore, the power of the study is 90% or 80%. This means that if there is a difference between groups, we want to be 80% (or 90%) certain that the study will detect that difference. For example, in the ABLE study, sample size was calculated with a type 1 error of 5% (two-sided) and power of 90% (type 2 error of 10%) (1).
Table 1 gives a summary of the two types of statistical errors with an example
Statistical errors
| (a) Types of statistical errors | |||
| : Null hypothesis is | |||
| True | False | ||
| Null hypothesis is actually | True | Correct results! | Falsely rejecting null hypothesis - Type I error |
| False | Falsely accepting null hypothesis - Type II error | Correct results! | |
| (b) Possible statistical errors in the ABLE trial | |||
| There is difference in mortality between groups receiving fresh RBCs and standard-issue RBCs | There difference in mortality between groups receiving fresh RBCs and standard-issue RBCs | ||
| Truth | There is difference in mortality between groups receiving fresh RBCs and standard-issue RBCs | Correct results! | Falsely rejecting null hypothesis - Type I error |
| There difference in mortality between groups receiving fresh RBCs and standard-issue RBCs | Falsely accepting null hypothesis - Type II error | Correct results! | |
In the next article in this series, we will look at the meaning and interpretation of ‘ p ’ value and confidence intervals for hypothesis testing.
Source of support: Nil
Conflict of interest: None
- Data Science
- Data Analysis
- Data Visualization
- Machine Learning
- Deep Learning
- Computer Vision
- Artificial Intelligence
- AI ML DS Interview Series
- AI ML DS Projects series
- Data Engineering
- Web Scrapping
- Explore GfG Premium
- Data Analysis with Python
Introduction to Data Analysis
- What is Data Analysis?
- Data Analytics and its type
- How to Install Numpy on Windows?
- How to Install Pandas in Python?
- How to Install Matplotlib on python?
- How to Install Python Tensorflow in Windows?
Data Analysis Libraries
- Pandas Tutorial
- NumPy Tutorial - Python Library
- Data Analysis with SciPy
- Introduction to TensorFlow
Data Visulization Libraries
- Matplotlib Tutorial
- Python Seaborn Tutorial
- Plotly tutorial
- Introduction to Bokeh in Python
Exploratory Data Analysis (EDA)
- Univariate, Bivariate and Multivariate data and its analysis
- Measures of Central Tendency in Statistics
- Measures of Spread - Range, Variance, and Standard Deviation
- Interquartile Range and Quartile Deviation using NumPy and SciPy
- Anova Formula
- Skewness of Statistical Data
- How to Calculate Skewness and Kurtosis in Python?
- Difference Between Skewness and Kurtosis
- Histogram | Meaning, Example, Types and Steps to Draw
- Interpretations of Histogram
- Quantile Quantile plots
- What is Univariate, Bivariate & Multivariate Analysis in Data Visualisation?
- Using pandas crosstab to create a bar plot
- Exploring Correlation in Python
- Covariance and Correlation
- Factor Analysis | Data Analysis
- Data Mining - Cluster Analysis
- MANOVA Test in R Programming
- Python - Central Limit Theorem
- Probability Distribution Function
- Probability Density Estimation & Maximum Likelihood Estimation
- Exponential Distribution in R Programming - dexp(), pexp(), qexp(), and rexp() Functions
- Mathematics | Probability Distributions Set 4 (Binomial Distribution)
- Poisson Distribution | Definition, Formula, Table and Examples
- P-Value: Comprehensive Guide to Understand, Apply, and Interpret
- Z-Score in Statistics
- How to Calculate Point Estimates in R?
- Confidence Interval
- Chi-square test in Machine Learning
Understanding Hypothesis Testing
Data preprocessing.
- ML | Data Preprocessing in Python
- ML | Overview of Data Cleaning
- ML | Handling Missing Values
- Detect and Remove the Outliers using Python
Data Transformation
- Data Normalization Machine Learning
- Sampling distribution Using Python
Time Series Data Analysis
- Data Mining - Time-Series, Symbolic and Biological Sequences Data
- Basic DateTime Operations in Python
- Time Series Analysis & Visualization in Python
- How to deal with missing values in a Timeseries in Python?
- How to calculate MOVING AVERAGE in a Pandas DataFrame?
- What is a trend in time series?
- How to Perform an Augmented Dickey-Fuller Test in R
- AutoCorrelation
Case Studies and Projects
- Top 8 Free Dataset Sources to Use for Data Science Projects
- Step by Step Predictive Analysis - Machine Learning
- 6 Tips for Creating Effective Data Visualizations
Hypothesis testing involves formulating assumptions about population parameters based on sample statistics and rigorously evaluating these assumptions against empirical evidence. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.
What is Hypothesis Testing?
A hypothesis is an assumption or idea, specifically a statistical claim about an unknown population parameter. For example, a judge assumes a person is innocent and verifies this by reviewing evidence and hearing testimony before reaching a verdict.
Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data.
To test the validity of the claim or assumption about the population parameter:
- A sample is drawn from the population and analyzed.
- The results of the analysis are used to decide whether the claim is true or not.
Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.
Defining Hypotheses
- Null hypothesis (H 0 ): In statistics, the null hypothesis is a general statement or default position that there is no relationship between two measured cases or no relationship among groups. In other words, it is a basic assumption or made based on the problem knowledge. Example : A company’s mean production is 50 units/per da H 0 : [Tex]\mu [/Tex] = 50.
- Alternative hypothesis (H 1 ): The alternative hypothesis is the hypothesis used in hypothesis testing that is contrary to the null hypothesis. Example: A company’s production is not equal to 50 units/per day i.e. H 1 : [Tex]\mu [/Tex] [Tex]\ne [/Tex] 50.
Key Terms of Hypothesis Testing
- Level of significance : It refers to the degree of significance in which we accept or reject the null hypothesis. 100% accuracy is not possible for accepting a hypothesis, so we, therefore, select a level of significance that is usually 5%. This is normally denoted with [Tex]\alpha[/Tex] and generally, it is 0.05 or 5%, which means your output should be 95% confident to give a similar kind of result in each sample.
- P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
- Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
- Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
- Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.
Why do we use Hypothesis Testing?
Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing.
One-Tailed and Two-Tailed Test
One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.
One-Tailed Test
There are two types of one-tailed test:
- Left-Tailed (Left-Sided) Test: The alternative hypothesis asserts that the true parameter value is less than the null hypothesis. Example: H 0 : [Tex]\mu \geq 50 [/Tex] and H 1 : [Tex]\mu < 50 [/Tex]
- Right-Tailed (Right-Sided) Test : The alternative hypothesis asserts that the true parameter value is greater than the null hypothesis. Example: H 0 : [Tex]\mu \leq50 [/Tex] and H 1 : [Tex]\mu > 50 [/Tex]
Two-Tailed Test
A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.
Example: H 0 : [Tex]\mu = [/Tex] 50 and H 1 : [Tex]\mu \neq 50 [/Tex]
To delve deeper into differences into both types of test: Refer to link
What are Type 1 and Type 2 errors in Hypothesis Testing?
In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.
- Type I error: When we reject the null hypothesis, although that hypothesis was true. Type I error is denoted by alpha( [Tex]\alpha [/Tex] ).
- Type II errors : When we accept the null hypothesis, but it is false. Type II errors are denoted by beta( [Tex]\beta [/Tex] ).
Null Hypothesis is True | Null Hypothesis is False | |
|---|---|---|
Null Hypothesis is True (Accept) | Correct Decision | Type II Error (False Negative) |
Alternative Hypothesis is True (Reject) | Type I Error (False Positive) | Correct Decision |
How does Hypothesis Testing work?
Step 1: define null and alternative hypothesis.
State the null hypothesis ( [Tex]H_0 [/Tex] ), representing no effect, and the alternative hypothesis ( [Tex]H_1 [/Tex] ), suggesting an effect or difference.
We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.
Step 2 – Choose significance level
Select a significance level ( [Tex]\alpha [/Tex] ), typically 0.05, to determine the threshold for rejecting the null hypothesis. It provides validity to our hypothesis test, ensuring that we have sufficient data to back up our claims. Usually, we determine our significance level beforehand of the test. The p-value is the criterion used to calculate our significance value.
Step 3 – Collect and Analyze data.
Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.
Step 4-Calculate Test Statistic
The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.
There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.
- Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
- t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
- Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
- F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.
We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.
T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.
Step 5 – Comparing Test Statistic:
In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.
Method A: Using Crtical values
Comparing the test statistic and tabulated critical value we have,
- If Test Statistic>Critical Value: Reject the null hypothesis.
- If Test Statistic≤Critical Value: Fail to reject the null hypothesis.
Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.
Method B: Using P-values
We can also come to an conclusion using the p-value,
- If the p-value is less than or equal to the significance level i.e. ( [Tex]p\leq\alpha [/Tex] ), you reject the null hypothesis. This indicates that the observed results are unlikely to have occurred by chance alone, providing evidence in favor of the alternative hypothesis.
- If the p-value is greater than the significance level i.e. ( [Tex]p\geq \alpha[/Tex] ), you fail to reject the null hypothesis. This suggests that the observed results are consistent with what would be expected under the null hypothesis.
Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.
Step 7- Interpret the Results
At last, we can conclude our experiment using method A or B.
Calculating test statistic
To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .
1. Z-statistics:
When population means and standard deviations are known.
[Tex]z = \frac{\bar{x} – \mu}{\frac{\sigma}{\sqrt{n}}}[/Tex]
- [Tex]\bar{x} [/Tex] is the sample mean,
- μ represents the population mean,
- σ is the standard deviation
- and n is the size of the sample.
2. T-Statistics
T test is used when n<30,
t-statistic calculation is given by:
[Tex]t=\frac{x̄-μ}{s/\sqrt{n}} [/Tex]
- t = t-score,
- x̄ = sample mean
- μ = population mean,
- s = standard deviation of the sample,
- n = sample size
3. Chi-Square Test
Chi-Square Test for Independence categorical Data (Non-normally distributed) using:
[Tex]\chi^2 = \sum \frac{(O_{ij} – E_{ij})^2}{E_{ij}}[/Tex]
- [Tex]O_{ij}[/Tex] is the observed frequency in cell [Tex]{ij} [/Tex]
- i,j are the rows and columns index respectively.
- [Tex]E_{ij}[/Tex] is the expected frequency in cell [Tex]{ij}[/Tex] , calculated as : [Tex]\frac{{\text{{Row total}} \times \text{{Column total}}}}{{\text{{Total observations}}}}[/Tex]
Real life Examples of Hypothesis Testing
Let’s examine hypothesis testing using two real life situations,
Case A: D oes a New Drug Affect Blood Pressure?
Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.
- Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
- After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114
Step 1 : Define the Hypothesis
- Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
- Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.
Step 2: Define the Significance level
Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.
If the evidence suggests less than a 5% chance of observing the results due to random variation.
Step 3 : Compute the test statistic
Using paired T-test analyze the data to obtain a test statistic and a p-value.
The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.
t = m/(s/√n)
- m = mean of the difference i.e X after, X before
- s = standard deviation of the difference (d) i.e d i = X after, i − X before,
- n = sample size,
then, m= -3.9, s= 1.8 and n= 10
we, calculate the , T-statistic = -9 based on the formula for paired t test
Step 4: Find the p-value
The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.
thus, p-value = 8.538051223166285e-06
Step 5: Result
- If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
- If the p-value is greater than 0.05, they fail to reject the null hypothesis.
Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.
Python Implementation of Case A
Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.
Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.
We will implement our first real life problem via python,
import numpy as np from scipy import stats # Data before_treatment = np . array ([ 120 , 122 , 118 , 130 , 125 , 128 , 115 , 121 , 123 , 119 ]) after_treatment = np . array ([ 115 , 120 , 112 , 128 , 122 , 125 , 110 , 117 , 119 , 114 ]) # Step 1: Null and Alternate Hypotheses # Null Hypothesis: The new drug has no effect on blood pressure. # Alternate Hypothesis: The new drug has an effect on blood pressure. null_hypothesis = "The new drug has no effect on blood pressure." alternate_hypothesis = "The new drug has an effect on blood pressure." # Step 2: Significance Level alpha = 0.05 # Step 3: Paired T-test t_statistic , p_value = stats . ttest_rel ( after_treatment , before_treatment ) # Step 4: Calculate T-statistic manually m = np . mean ( after_treatment - before_treatment ) s = np . std ( after_treatment - before_treatment , ddof = 1 ) # using ddof=1 for sample standard deviation n = len ( before_treatment ) t_statistic_manual = m / ( s / np . sqrt ( n )) # Step 5: Decision if p_value <= alpha : decision = "Reject" else : decision = "Fail to reject" # Conclusion if decision == "Reject" : conclusion = "There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different." else : conclusion = "There is insufficient evidence to claim a significant difference in average blood pressure before and after treatment with the new drug." # Display results print ( "T-statistic (from scipy):" , t_statistic ) print ( "P-value (from scipy):" , p_value ) print ( "T-statistic (calculated manually):" , t_statistic_manual ) print ( f "Decision: { decision } the null hypothesis at alpha= { alpha } ." ) print ( "Conclusion:" , conclusion )
T-statistic (from scipy): -9.0 P-value (from scipy): 8.538051223166285e-06 T-statistic (calculated manually): -9.0 Decision: Reject the null hypothesis at alpha=0.05. Conclusion: There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.
In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05.
- The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
- The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.
Case B : Cholesterol level in a population
Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.
Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.
Populations Mean = 200
Population Standard Deviation (σ): 5 mg/dL(given for this problem)
Step 1: Define the Hypothesis
- Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
- Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.
As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.
The test statistic is calculated by using the z formula Z = [Tex](203.8 – 200) / (5 \div \sqrt{25}) [/Tex] and we get accordingly , Z =2.039999999999992.
Step 4: Result
Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL
Python Implementation of Case B
import scipy.stats as stats import math import numpy as np # Given data sample_data = np . array ( [ 205 , 198 , 210 , 190 , 215 , 205 , 200 , 192 , 198 , 205 , 198 , 202 , 208 , 200 , 205 , 198 , 205 , 210 , 192 , 205 , 198 , 205 , 210 , 192 , 205 ]) population_std_dev = 5 population_mean = 200 sample_size = len ( sample_data ) # Step 1: Define the Hypotheses # Null Hypothesis (H0): The average cholesterol level in a population is 200 mg/dL. # Alternate Hypothesis (H1): The average cholesterol level in a population is different from 200 mg/dL. # Step 2: Define the Significance Level alpha = 0.05 # Two-tailed test # Critical values for a significance level of 0.05 (two-tailed) critical_value_left = stats . norm . ppf ( alpha / 2 ) critical_value_right = - critical_value_left # Step 3: Compute the test statistic sample_mean = sample_data . mean () z_score = ( sample_mean - population_mean ) / \ ( population_std_dev / math . sqrt ( sample_size )) # Step 4: Result # Check if the absolute value of the test statistic is greater than the critical values if abs ( z_score ) > max ( abs ( critical_value_left ), abs ( critical_value_right )): print ( "Reject the null hypothesis." ) print ( "There is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL." ) else : print ( "Fail to reject the null hypothesis." ) print ( "There is not enough evidence to conclude that the average cholesterol level in the population is different from 200 mg/dL." )
Reject the null hypothesis. There is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL.
Limitations of Hypothesis Testing
- Although a useful technique, hypothesis testing does not offer a comprehensive grasp of the topic being studied. Without fully reflecting the intricacy or whole context of the phenomena, it concentrates on certain hypotheses and statistical significance.
- The accuracy of hypothesis testing results is contingent on the quality of available data and the appropriateness of statistical methods used. Inaccurate data or poorly formulated hypotheses can lead to incorrect conclusions.
- Relying solely on hypothesis testing may cause analysts to overlook significant patterns or relationships in the data that are not captured by the specific hypotheses being tested. This limitation underscores the importance of complimenting hypothesis testing with other analytical approaches.
Hypothesis testing stands as a cornerstone in statistical analysis, enabling data scientists to navigate uncertainties and draw credible inferences from sample data. By systematically defining null and alternative hypotheses, choosing significance levels, and leveraging statistical tests, researchers can assess the validity of their assumptions. The article also elucidates the critical distinction between Type I and Type II errors, providing a comprehensive understanding of the nuanced decision-making process inherent in hypothesis testing. The real-life example of testing a new drug’s effect on blood pressure using a paired T-test showcases the practical application of these principles, underscoring the importance of statistical rigor in data-driven decision-making.
Frequently Asked Questions (FAQs)
1. what are the 3 types of hypothesis test.
There are three types of hypothesis tests: right-tailed, left-tailed, and two-tailed. Right-tailed tests assess if a parameter is greater, left-tailed if lesser. Two-tailed tests check for non-directional differences, greater or lesser.
2.What are the 4 components of hypothesis testing?
Null Hypothesis ( [Tex]H_o [/Tex] ): No effect or difference exists. Alternative Hypothesis ( [Tex]H_1 [/Tex] ): An effect or difference exists. Significance Level ( [Tex]\alpha [/Tex] ): Risk of rejecting null hypothesis when it’s true (Type I error). Test Statistic: Numerical value representing observed evidence against null hypothesis.
3.What is hypothesis testing in ML?
Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.
4.What is the difference between Pytest and hypothesis in Python?
Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.
Please Login to comment...
Similar reads.
- data-science
Improve your Coding Skills with Practice
What kind of Experience do you want to share?

- History & Society
- Science & Tech
- Biographies
- Animals & Nature
- Geography & Travel
- Arts & Culture
- Games & Quizzes
- On This Day
- One Good Fact
- New Articles
- Lifestyles & Social Issues
- Philosophy & Religion
- Politics, Law & Government
- World History
- Health & Medicine
- Browse Biographies
- Birds, Reptiles & Other Vertebrates
- Bugs, Mollusks & Other Invertebrates
- Environment
- Fossils & Geologic Time
- Entertainment & Pop Culture
- Sports & Recreation
- Visual Arts
- Demystified
- Image Galleries
- Infographics
- Top Questions
- Britannica Kids
- Saving Earth
- Space Next 50
- Student Center
- Introduction
- Tabular methods
- Graphical methods
- Exploratory data analysis
- Events and their probabilities
- Random variables and probability distributions
- The binomial distribution
- The Poisson distribution
- The normal distribution
- Sampling and sampling distributions
- Estimation of a population mean
- Estimation of other parameters
- Estimation procedures for two populations
Hypothesis testing
Bayesian methods.
- Analysis of variance and significance testing
- Regression model
- Least squares method
- Analysis of variance and goodness of fit
- Significance testing
- Residual analysis
- Model building
- Correlation
- Time series and forecasting
- Nonparametric methods
- Acceptance sampling
- Statistical process control
- Sample survey methods
- Decision analysis
Our editors will review what you’ve submitted and determine whether to revise the article.
- Arizona State University - Educational Outreach and Student Services - Basic Statistics
- Princeton University - Probability and Statistics
- Statistics LibreTexts - Introduction to Statistics
- University of North Carolina at Chapel Hill - The Writing Center - Statistics
- Corporate Finance Institute - Statistics
- statistics - Children's Encyclopedia (Ages 8-11)
- statistics - Student Encyclopedia (Ages 11 and up)
- Table Of Contents
Hypothesis testing is a form of statistical inference that uses data from a sample to draw conclusions about a population parameter or a population probability distribution . First, a tentative assumption is made about the parameter or distribution. This assumption is called the null hypothesis and is denoted by H 0 . An alternative hypothesis (denoted H a ), which is the opposite of what is stated in the null hypothesis, is then defined. The hypothesis-testing procedure involves using sample data to determine whether or not H 0 can be rejected. If H 0 is rejected, the statistical conclusion is that the alternative hypothesis H a is true.
Recent News
For example, assume that a radio station selects the music it plays based on the assumption that the average age of its listening audience is 30 years. To determine whether this assumption is valid, a hypothesis test could be conducted with the null hypothesis given as H 0 : μ = 30 and the alternative hypothesis given as H a : μ ≠ 30. Based on a sample of individuals from the listening audience, the sample mean age, x̄ , can be computed and used to determine whether there is sufficient statistical evidence to reject H 0 . Conceptually, a value of the sample mean that is “close” to 30 is consistent with the null hypothesis, while a value of the sample mean that is “not close” to 30 provides support for the alternative hypothesis. What is considered “close” and “not close” is determined by using the sampling distribution of x̄ .
Ideally, the hypothesis-testing procedure leads to the acceptance of H 0 when H 0 is true and the rejection of H 0 when H 0 is false. Unfortunately, since hypothesis tests are based on sample information, the possibility of errors must be considered. A type I error corresponds to rejecting H 0 when H 0 is actually true, and a type II error corresponds to accepting H 0 when H 0 is false. The probability of making a type I error is denoted by α, and the probability of making a type II error is denoted by β.
In using the hypothesis-testing procedure to determine if the null hypothesis should be rejected, the person conducting the hypothesis test specifies the maximum allowable probability of making a type I error, called the level of significance for the test. Common choices for the level of significance are α = 0.05 and α = 0.01. Although most applications of hypothesis testing control the probability of making a type I error, they do not always control the probability of making a type II error. A graph known as an operating-characteristic curve can be constructed to show how changes in the sample size affect the probability of making a type II error.
A concept known as the p -value provides a convenient basis for drawing conclusions in hypothesis-testing applications. The p -value is a measure of how likely the sample results are, assuming the null hypothesis is true; the smaller the p -value, the less likely the sample results. If the p -value is less than α, the null hypothesis can be rejected; otherwise, the null hypothesis cannot be rejected. The p -value is often called the observed level of significance for the test.
A hypothesis test can be performed on parameters of one or more populations as well as in a variety of other situations. In each instance, the process begins with the formulation of null and alternative hypotheses about the population. In addition to the population mean, hypothesis-testing procedures are available for population parameters such as proportions, variances , standard deviations , and medians .
Hypothesis tests are also conducted in regression and correlation analysis to determine if the regression relationship and the correlation coefficient are statistically significant (see below Regression and correlation analysis ). A goodness-of-fit test refers to a hypothesis test in which the null hypothesis is that the population has a specific probability distribution, such as a normal probability distribution. Nonparametric statistical methods also involve a variety of hypothesis-testing procedures.
The methods of statistical inference previously described are often referred to as classical methods. Bayesian methods (so called after the English mathematician Thomas Bayes ) provide alternatives that allow one to combine prior information about a population parameter with information contained in a sample to guide the statistical inference process. A prior probability distribution for a parameter of interest is specified first. Sample information is then obtained and combined through an application of Bayes’s theorem to provide a posterior probability distribution for the parameter. The posterior distribution provides the basis for statistical inferences concerning the parameter.
A key, and somewhat controversial, feature of Bayesian methods is the notion of a probability distribution for a population parameter. According to classical statistics, parameters are constants and cannot be represented as random variables. Bayesian proponents argue that, if a parameter value is unknown, then it makes sense to specify a probability distribution that describes the possible values for the parameter as well as their likelihood . The Bayesian approach permits the use of objective data or subjective opinion in specifying a prior distribution. With the Bayesian approach, different individuals might specify different prior distributions. Classical statisticians argue that for this reason Bayesian methods suffer from a lack of objectivity. Bayesian proponents argue that the classical methods of statistical inference have built-in subjectivity (through the choice of a sampling plan) and that the advantage of the Bayesian approach is that the subjectivity is made explicit.
Bayesian methods have been used extensively in statistical decision theory (see below Decision analysis ). In this context , Bayes’s theorem provides a mechanism for combining a prior probability distribution for the states of nature with sample information to provide a revised (posterior) probability distribution about the states of nature. These posterior probabilities are then used to make better decisions.
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Test Statistic: Definition, Types & Formulas
By Jim Frost 10 Comments
What is a Test Statistic?
A test statistic assesses how consistent your sample data are with the null hypothesis in a hypothesis test. Test statistic calculations take your sample data and boil them down to a single number that quantifies how much your sample diverges from the null hypothesis. As a test statistic value becomes more extreme, it indicates larger differences between your sample data and the null hypothesis.
When your test statistic indicates a sufficiently large incompatibility with the null hypothesis, you can reject the null and state that your results are statistically significant—your data support the notion that the sample effect exists in the population . To use a test statistic to evaluate statistical significance, you either compare it to a critical value or use it to calculate the p-value .
Statisticians named the hypothesis tests after the test statistics because they’re the quantity that the tests actually evaluate. For example, t-tests assess t-values, F-tests evaluate F-values, and chi-square tests use, you guessed it, chi-square values.
In this post, learn about test statistics, how to calculate them, interpret them, and evaluate statistical significance using the critical value and p-value methods.
How to Find Test Statistics
Each test statistic has its own formula. I present several common test statistics examples below. To see worked examples for each one, click the links to my more detailed articles.
Formulas for Test Statistics
| T-value for 1-sample t-test | Take the sample mean, subtract the hypothesized mean, and divide by the . | |
| T-value for 2-sample t-test | Take one sample mean, subtract the other, and divide by the pooled standard deviation. | |
| F-value for F-tests and ANOVA | Calculate the ratio of two . | |
| Chi-squared value (χ ) for a Chi-squared test | Sum the squared differences between observed and expected values divided by the expected values. |
Understanding the Null Values and the Test Statistic Formulas
In the formulas above, it’s helpful to understand the null condition and the test statistic value that occurs when your sample data match that condition exactly. Also, it’s worthwhile knowing what causes the test statistics to move further away from the null value, potentially becoming significant. Test statistics are statistically significant when they exceed a critical value.
All these test statistics are ratios, which helps you understand their null values.
T-Tests, Null = 0
When a t-value equals 0, it indicates that your sample data match the null hypothesis exactly.
For a 1-sample t-test, when the sample mean equals the hypothesized mean, the numerator is zero, which causes the entire t-value ratio to equal zero. As the sample mean moves away from the hypothesized mean in either the positive or negative direction, the test statistic moves away from zero in the same direction.
A similar case exists for 2-sample t-tests. When the two sample means are equal, the numerator is zero, and the entire test statistic ratio is zero. As the two sample means become increasingly different, the absolute value of the numerator increases, and the t-value becomes more positive or negative.
Related post : How T-tests Work
F-tests including ANOVA, Null = 1
When an F-value equals 1, it indicates that the two variances in the numerator and denominator are equal, matching the null hypothesis.
As the numerator and denominator become less and less similar, the F-value moves away from one in either direction.
Related post : The F-test in ANOVA
Chi-squared Tests, Null = 0
When a chi-squared value equals 0, it indicates that the observed values always match the expected values. This condition causes the numerator to equal zero, making the chi-squared value equal zero.
As the observed values progressively fail to match the expected values, the numerator increases, causing the test statistic to rise from zero.
Related post : How a Chi-Squared Test Works
You’ll never see a test statistic that equals the null value precisely in practice. However, trivial differences been sample values and the null value are not uncommon.
Interpreting Test Statistics
Test statistics are unitless. This fact can make them difficult to interpret on their own. You know they evaluate how well your data agree with the null hypothesis. If your test statistic is extreme enough, your data are so incompatible with the null hypothesis that you can reject it and conclude that your results are statistically significant. But how does that translate to specific values of your test statistic? Where do you draw the line?
For instance, t-values of zero match the null value. But how far from zero should your t-value be to be statistically significant? Is 1 enough? 2? 3? If your t-value is 2, what does it mean anyway? In this case, we know that the sample mean doesn’t equal the null value, but how exceptional is it? To complicate matters, the dividing line changes depending on your sample size and other study design issues.
Similar types of questions apply to the other test statistics too.
To interpret individual values of a test statistic, we need to place them in a larger context. Towards this end, let me introduce you to sampling distributions for test statistics!
Sampling Distributions for Test Statistics
Performing a hypothesis test on a sample produces a single test statistic. Now, imagine you carry out the following process:
- Assume the null hypothesis is true in the population.
- Repeat your study many times by drawing many random samples of the same size from this population.
- Perform the same hypothesis test on all these samples and save the test statistics.
- Plot the distribution of the test statistics.
This process produces the distribution of test statistic values that occurs when the effect does not exist in the population (i.e., the null hypothesis is true). Statisticians refer to this type of distribution as a sampling distribution, a kind of probability distribution.
Why would we need this type of distribution?
It provides the larger context required for interpreting a test statistic. More specifically, it allows us to compare our study’s single test statistic to values likely to occur when the null is true. We can quantify our sample statistic’s rareness while assuming the effect does not exist in the population. Now that’s helpful!
Fortunately, we don’t need to collect many random samples to create this distribution! Statisticians have developed formulas allowing us to estimate sampling distributions for test statistics using the sample data.
To evaluate your data’s compatibility with the null hypothesis, place your study’s test statistic in the distribution.
Related post : Understanding Probability Distributions
Example of a Test Statistic in a Sampling Distribution
Suppose our t-test produces a t-value of two. That’s our test statistic. Let’s see where it fits in.
The sampling distribution below shows a t-distribution with 20 degrees of freedom, equating to a 1-sample t-test with a sample size of 21. The distribution centers on zero because it assumes the null hypothesis is correct. When the null is true, your analysis is most likely to obtain a t-value near zero and less likely to produce t-values further from zero in either direction.

The sampling distribution indicates that our test statistic is somewhat rare when we assume the null hypothesis is correct. However, the chances of observing t-values from -2 to +2 are not totally inconceivable. We need a way to quantify the likelihood.
From this point, we need to use the sampling distributions’ ability to calculate probabilities for test statistics.
Related post : Sampling Distributions Explained
Test Statistics and Critical Values
The significance level uses critical values to define how far the test statistic must be from the null value to reject the null hypothesis. When the test statistic exceeds a critical value, the results are statistically significant.
The percentage of the area beneath the sampling distribution curve that is shaded represents the probability that the test statistic will fall in those regions when the null is true. Consequently, to depict a significance level of 0.05, I’ll shade 5% of the sampling distribution furthest away from the null value.
The two shaded areas are equidistant from the null value in the center. Each region has a likelihood of 0.025, which sums to our significance level of 0.05. These shaded areas are the critical regions for a two-tailed hypothesis test. Let’s return to our example t-value of 2.
Related post : What are Critical Values?

In this example, the critical values are -2.086 and +2.086. Our test statistic of 2 is not statistically significant because it does not exceed the critical value.
Other hypothesis tests have their own test statistics and sampling distributions, but their processes for critical values are generally similar.
Learn how to find critical values for test statistics using tables:
- T-distribution table
- Chi-square table
Related post : Understanding Significance Levels
Using Test Statistics to Find P-values
P-values are the probability of observing an effect at least as extreme as your sample’s effect if you assume no effect exists in the population.
Test statistics represent effect sizes in hypothesis tests because they denote the difference between your sample effect and no effect —the null hypothesis. Consequently, you use the test statistic to calculate the p-value for your hypothesis test.
The above p-value definition is a bit tortuous. Fortunately, it’s much easier to understand how test statistics and p-values work together using a sampling distribution graph.
Let’s use our hypothetical test statistic t-value of 2 for this example. However, because I’m displaying the results of a two-tailed test, I need to use t-values of +2 and -2 to cover both tails.
Related post : One-tailed vs. Two-Tailed Hypothesis Tests
The graph below displays the probability of t-values less than -2 and greater than +2 using the area under the curve. This graph is specific to our t-test design (1-sample t-test with N = 21).

The sampling distribution indicates that each of the two shaded regions has a probability of 0.02963—for a total of 0.05926. That’s the p-value! The graph shows that the test statistic falls within these areas almost 6% of the time when the null hypothesis is true in the population.
While this likelihood seems small, it’s not low enough to justify rejecting the null under the standard significance level of 0.05. P-value results are always consistent with the critical value method. Learn more about using test statistics to find p values .
While test statistics are a crucial part of hypothesis testing, you’ll probably let your statistical software calculate the p-value for the test. However, understanding test statistics will boost your comprehension of what a hypothesis test actually assesses.
Related post : Interpreting P-values
Share this:

Reader Interactions
July 5, 2024 at 8:21 am
“As the observed values progressively fail to match the observed values, the numerator increases, causing the test statistic to rise from zero”.
Sir, this sentence is written in the Chi-squared Test heading. There the observed value is written twice. I think the second one to be replaced with ‘expected values’.
July 5, 2024 at 4:10 pm
Thanks so much, Dr. Raj. You’re correct about the typo and I’ve made the correction.
May 9, 2024 at 1:40 am
Thank you very much (great page on one and two-tailed tests)!
May 6, 2024 at 12:17 pm
I would like to ask a question. If only positive numbers are the possible values in a sample (e.g. absolute values without 0), is it meaningful to test if the sample is significantly different from zero (using for example a one sample t-test or a Wilcoxon signed-rank test) or can I assume that if given a large enough sample, the result will by definition be significant (even if a small or very variable sample results in a non-significant hypothesis test).
Thank you very much,
May 6, 2024 at 4:35 pm
If you’re talking about the raw values you’re assessing using a one-sample t-test, it doesn’t make sense to compare them to zero given your description of the data. You know that the mean can’t possibly equal zero. The mean must be some positive value. Yes, in this scenario, if you have a large enough sample size, you should get statistically significant results. So, that t-test isn’t tell you anything that you don’t already know!
However, you should be aware of several things. The 1-sample test can compare your sample mean to values other than zero. Typically, you’ll need to specify the value of the null hypothesis for your software. This value is the comparison value. The test determines whether your sample data provide enough evidence to conclude that the population mean does not equal the null hypothesis value you specify. You’ll need to specify the value because there is no obvious default value to use. Every 1-sample t-test has its subject-area context with a value that makes sense for its null hypothesis value and it is frequently not zero.
I suspect that you’re getting tripped up with the fact that t-tests use a t-value of zero for its null hypothesis value. That doesn’t mean your 1-sample t-test is comparing your sample mean to zero. The test converts your data to a single t-value and compares the t-value to zero. But your actual null hypothesis value can be something else. It’s just converting your sample to a standardized value to use for testing. So, while the t-test compares your sample’s t-value to zero, you can actually compare your sample mean to any value you specify. You need to use a value that makes sense for your subject area.
I hope that makes sense!
May 8, 2024 at 8:37 am
Thank you very much Jim, this helps a lot! Actually, the value I would like to compare my sample to is zero, but I just couldn’t find the right way to test it apparently (it’s about EEG data). The original data was a sample of numbers between -1 and +1, with the question if they are significantly different from zero in either direction (in which case a one sample t-test makes sense I guess, since the sample mean can in fact be zero). However, since a sample mean of 0 can also occur if half of the sample differs in the negative, and the other half in the positive direction, I also wanted to test if there is a divergence from 0 in ‘absolute’ terms – that’s how the absolute valued numbers came about (I know that absolute values can also be zero, but in this specific case, they were all positive numbers) And a special thanks for the last paragraph – I will definitely keep in mind, it is a potential point of confusion.
May 8, 2024 at 8:33 pm
You can use a 1-sample t test for both cases but you’ll need to set them up slightly different. To detect a positive or negative difference from zero, use a 2-tailed test. For the case with absolute values, use a one-tailed test with a critical region in the positive end. To learn more, read about One- and Two-Tailed Tests Explained . Use zero for the comparison value in both cases.
February 12, 2024 at 1:00 am
Very helpful and well articulated! Thanks Jim 🙂
September 18, 2023 at 10:01 am
Thank you for brief explanation.
July 25, 2022 at 8:32 am
the content was helpful to me. thank you
Comments and Questions Cancel reply
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
- Choosing the Right Statistical Test | Types & Examples
Choosing the Right Statistical Test | Types & Examples
Published on January 28, 2020 by Rebecca Bevans . Revised on June 22, 2023.
Statistical tests are used in hypothesis testing . They can be used to:
- determine whether a predictor variable has a statistically significant relationship with an outcome variable.
- estimate the difference between two or more groups.
Statistical tests assume a null hypothesis of no relationship or no difference between groups. Then they determine whether the observed data fall outside of the range of values predicted by the null hypothesis.
If you already know what types of variables you’re dealing with, you can use the flowchart to choose the right statistical test for your data.
Statistical tests flowchart
Table of contents
What does a statistical test do, when to perform a statistical test, choosing a parametric test: regression, comparison, or correlation, choosing a nonparametric test, flowchart: choosing a statistical test, other interesting articles, frequently asked questions about statistical tests.
Statistical tests work by calculating a test statistic – a number that describes how much the relationship between variables in your test differs from the null hypothesis of no relationship.
It then calculates a p value (probability value). The p -value estimates how likely it is that you would see the difference described by the test statistic if the null hypothesis of no relationship were true.
If the value of the test statistic is more extreme than the statistic calculated from the null hypothesis, then you can infer a statistically significant relationship between the predictor and outcome variables.
If the value of the test statistic is less extreme than the one calculated from the null hypothesis, then you can infer no statistically significant relationship between the predictor and outcome variables.
Prevent plagiarism. Run a free check.
You can perform statistical tests on data that have been collected in a statistically valid manner – either through an experiment , or through observations made using probability sampling methods .
For a statistical test to be valid , your sample size needs to be large enough to approximate the true distribution of the population being studied.
To determine which statistical test to use, you need to know:
- whether your data meets certain assumptions.
- the types of variables that you’re dealing with.
Statistical assumptions
Statistical tests make some common assumptions about the data they are testing:
- Independence of observations (a.k.a. no autocorrelation): The observations/variables you include in your test are not related (for example, multiple measurements of a single test subject are not independent, while measurements of multiple different test subjects are independent).
- Homogeneity of variance : the variance within each group being compared is similar among all groups. If one group has much more variation than others, it will limit the test’s effectiveness.
- Normality of data : the data follows a normal distribution (a.k.a. a bell curve). This assumption applies only to quantitative data .
If your data do not meet the assumptions of normality or homogeneity of variance, you may be able to perform a nonparametric statistical test , which allows you to make comparisons without any assumptions about the data distribution.
If your data do not meet the assumption of independence of observations, you may be able to use a test that accounts for structure in your data (repeated-measures tests or tests that include blocking variables).
Types of variables
The types of variables you have usually determine what type of statistical test you can use.
Quantitative variables represent amounts of things (e.g. the number of trees in a forest). Types of quantitative variables include:
- Continuous (aka ratio variables): represent measures and can usually be divided into units smaller than one (e.g. 0.75 grams).
- Discrete (aka integer variables): represent counts and usually can’t be divided into units smaller than one (e.g. 1 tree).
Categorical variables represent groupings of things (e.g. the different tree species in a forest). Types of categorical variables include:
- Ordinal : represent data with an order (e.g. rankings).
- Nominal : represent group names (e.g. brands or species names).
- Binary : represent data with a yes/no or 1/0 outcome (e.g. win or lose).
Choose the test that fits the types of predictor and outcome variables you have collected (if you are doing an experiment , these are the independent and dependent variables ). Consult the tables below to see which test best matches your variables.
Parametric tests usually have stricter requirements than nonparametric tests, and are able to make stronger inferences from the data. They can only be conducted with data that adheres to the common assumptions of statistical tests.
The most common types of parametric test include regression tests, comparison tests, and correlation tests.
Regression tests
Regression tests look for cause-and-effect relationships . They can be used to estimate the effect of one or more continuous variables on another variable.
| Predictor variable | Outcome variable | Research question example | |
|---|---|---|---|
| What is the effect of income on longevity? | |||
| What is the effect of income and minutes of exercise per day on longevity? | |||
| Logistic regression | What is the effect of drug dosage on the survival of a test subject? |
Comparison tests
Comparison tests look for differences among group means . They can be used to test the effect of a categorical variable on the mean value of some other characteristic.
T-tests are used when comparing the means of precisely two groups (e.g., the average heights of men and women). ANOVA and MANOVA tests are used when comparing the means of more than two groups (e.g., the average heights of children, teenagers, and adults).
| Predictor variable | Outcome variable | Research question example | |
|---|---|---|---|
| Paired t-test | What is the effect of two different test prep programs on the average exam scores for students from the same class? | ||
| Independent t-test | What is the difference in average exam scores for students from two different schools? | ||
| ANOVA | What is the difference in average pain levels among post-surgical patients given three different painkillers? | ||
| MANOVA | What is the effect of flower species on petal length, petal width, and stem length? |
Correlation tests
Correlation tests check whether variables are related without hypothesizing a cause-and-effect relationship.
These can be used to test whether two variables you want to use in (for example) a multiple regression test are autocorrelated.
| Variables | Research question example | |
|---|---|---|
| Pearson’s | How are latitude and temperature related? |
Non-parametric tests don’t make as many assumptions about the data, and are useful when one or more of the common statistical assumptions are violated. However, the inferences they make aren’t as strong as with parametric tests.
| Predictor variable | Outcome variable | Use in place of… | |
|---|---|---|---|
| Spearman’s | |||
| Pearson’s | |||
| Sign test | One-sample -test | ||
| Kruskal–Wallis | ANOVA | ||
| ANOSIM | MANOVA | ||
| Wilcoxon Rank-Sum test | Independent t-test | ||
| Wilcoxon Signed-rank test | Paired t-test | ||
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example
This flowchart helps you choose among parametric tests. For nonparametric alternatives, check the table above.
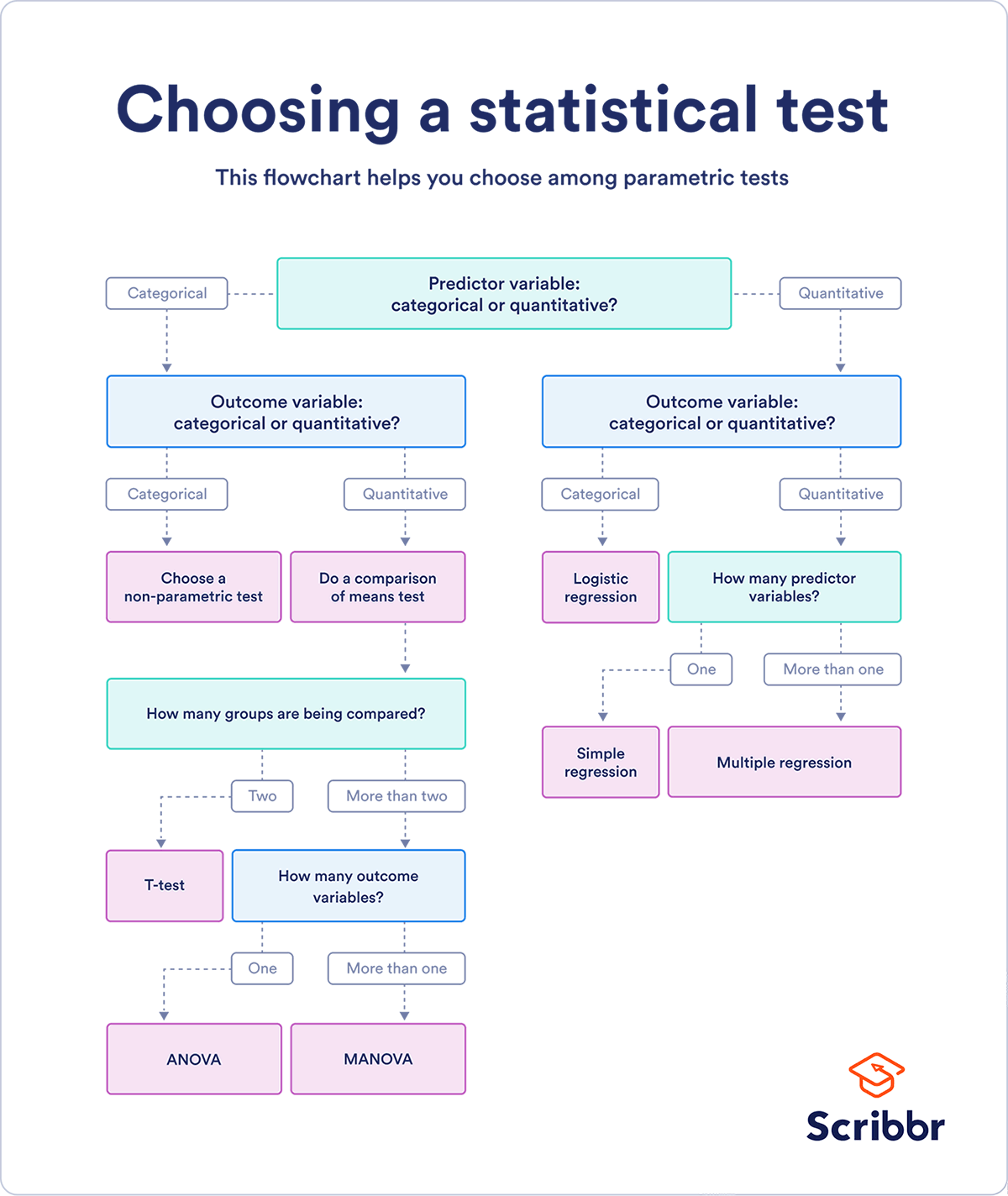
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
- Null hypothesis
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Statistical tests commonly assume that:
- the data are normally distributed
- the groups that are being compared have similar variance
- the data are independent
If your data does not meet these assumptions you might still be able to use a nonparametric statistical test , which have fewer requirements but also make weaker inferences.
A test statistic is a number calculated by a statistical test . It describes how far your observed data is from the null hypothesis of no relationship between variables or no difference among sample groups.
The test statistic tells you how different two or more groups are from the overall population mean , or how different a linear slope is from the slope predicted by a null hypothesis . Different test statistics are used in different statistical tests.
Statistical significance is a term used by researchers to state that it is unlikely their observations could have occurred under the null hypothesis of a statistical test . Significance is usually denoted by a p -value , or probability value.
Statistical significance is arbitrary – it depends on the threshold, or alpha value, chosen by the researcher. The most common threshold is p < 0.05, which means that the data is likely to occur less than 5% of the time under the null hypothesis .
When the p -value falls below the chosen alpha value, then we say the result of the test is statistically significant.
Quantitative variables are any variables where the data represent amounts (e.g. height, weight, or age).
Categorical variables are any variables where the data represent groups. This includes rankings (e.g. finishing places in a race), classifications (e.g. brands of cereal), and binary outcomes (e.g. coin flips).
You need to know what type of variables you are working with to choose the right statistical test for your data and interpret your results .
Discrete and continuous variables are two types of quantitative variables :
- Discrete variables represent counts (e.g. the number of objects in a collection).
- Continuous variables represent measurable amounts (e.g. water volume or weight).
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bevans, R. (2023, June 22). Choosing the Right Statistical Test | Types & Examples. Scribbr. Retrieved August 5, 2024, from https://www.scribbr.com/statistics/statistical-tests/
Is this article helpful?
Rebecca Bevans
Other students also liked, hypothesis testing | a step-by-step guide with easy examples, test statistics | definition, interpretation, and examples, normal distribution | examples, formulas, & uses, what is your plagiarism score.
User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
1.2 - the 7 step process of statistical hypothesis testing.
We will cover the seven steps one by one.
Step 1: State the Null Hypothesis
The null hypothesis can be thought of as the opposite of the "guess" the researchers made. In the example presented in the previous section, the biologist "guesses" plant height will be different for the various fertilizers. So the null hypothesis would be that there will be no difference among the groups of plants. Specifically, in more statistical language the null for an ANOVA is that the means are the same. We state the null hypothesis as:
\(H_0 \colon \mu_1 = \mu_2 = ⋯ = \mu_T\)
for T levels of an experimental treatment.
Step 2: State the Alternative Hypothesis
\(H_A \colon \text{ treatment level means not all equal}\)
The alternative hypothesis is stated in this way so that if the null is rejected, there are many alternative possibilities.
For example, \(\mu_1\ne \mu_2 = ⋯ = \mu_T\) is one possibility, as is \(\mu_1=\mu_2\ne\mu_3= ⋯ =\mu_T\). Many people make the mistake of stating the alternative hypothesis as \(\mu_1\ne\mu_2\ne⋯\ne\mu_T\) which says that every mean differs from every other mean. This is a possibility, but only one of many possibilities. A simple way of thinking about this is that at least one mean is different from all others. To cover all alternative outcomes, we resort to a verbal statement of "not all equal" and then follow up with mean comparisons to find out where differences among means exist. In our example, a possible outcome would be that fertilizer 1 results in plants that are exceptionally tall, but fertilizers 2, 3, and the control group may not differ from one another.
Step 3: Set \(\alpha\)
If we look at what can happen in a hypothesis test, we can construct the following contingency table:
| Decision | In Reality | |
|---|---|---|
| \(H_0\) is TRUE | \(H_0\) is FALSE | |
| Accept \(H_0\) | correct | Type II Error \(\beta\) = probability of Type II Error |
| Reject \(H_0\) | Type I Error | correct |
You should be familiar with Type I and Type II errors from your introductory courses. It is important to note that we want to set \(\alpha\) before the experiment ( a-priori ) because the Type I error is the more grievous error to make. The typical value of \(\alpha\) is 0.05, establishing a 95% confidence level. For this course, we will assume \(\alpha\) =0.05, unless stated otherwise.
Step 4: Collect Data
Remember the importance of recognizing whether data is collected through an experimental design or observational study.
Step 5: Calculate a test statistic
For categorical treatment level means, we use an F- statistic, named after R.A. Fisher. We will explore the mechanics of computing the F- statistic beginning in Lesson 2. The F- value we get from the data is labeled \(F_{\text{calculated}}\).
Step 6: Construct Acceptance / Rejection regions
As with all other test statistics, a threshold (critical) value of F is established. This F- value can be obtained from statistical tables or software and is referred to as \(F_{\text{critical}}\) or \(F_\alpha\). As a reminder, this critical value is the minimum value of the test statistic (in this case \(F_{\text{calculated}}\)) for us to reject the null.
The F- distribution, \(F_\alpha\), and the location of acceptance/rejection regions are shown in the graph below:
Step 7: Based on Steps 5 and 6, draw a conclusion about \(H_0\)
If \(F_{\text{calculated}}\) is larger than \(F_\alpha\), then you are in the rejection region and you can reject the null hypothesis with \(\left(1-\alpha \right)\) level of confidence.
Note that modern statistical software condenses Steps 6 and 7 by providing a p -value. The p -value here is the probability of getting an \(F_{\text{calculated}}\) even greater than what you observe assuming the null hypothesis is true. If by chance, the \(F_{\text{calculated}} = F_\alpha\), then the p -value would be exactly equal to \(\alpha\). With larger \(F_{\text{calculated}}\) values, we move further into the rejection region and the p- value becomes less than \(\alpha\). So, the decision rule is as follows:
If the p- value obtained from the ANOVA is less than \(\alpha\), then reject \(H_0\) in favor of \(H_A\).

IMAGES
VIDEO
COMMENTS
Present the findings in your results and discussion section. Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps. Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test.
Hypothesis testing is a statistical method used to determine if there is enough evidence in a sample data to draw conclusions about a population. It involves formulating two competing hypotheses, the null hypothesis (H0) and the alternative hypothesis (Ha), and then collecting data to assess the evidence.
Statistical hypothesis testing is a key technique of both frequentist inference and Bayesian inference, although the two types of inference have notable differences. Statistical hypothesis tests define a procedure that controls (fixes) the probability of incorrectly deciding that a default position (null hypothesis) is incorrect. The procedure ...
The researchers write their hypotheses. These statements apply to the population, so they use the mu (μ) symbol for the population mean parameter.. Null Hypothesis (H 0): The population means of the test scores for the two groups are equal (μ 1 = μ 2).; Alternative Hypothesis (H A): The population means of the test scores for the two groups are unequal (μ 1 ≠ μ 2).
A statistical hypothesis is an assumption about a population parameter.. For example, we may assume that the mean height of a male in the U.S. is 70 inches. The assumption about the height is the statistical hypothesis and the true mean height of a male in the U.S. is the population parameter.. A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical ...
Hypothesis testing is an act in statistics whereby an analyst tests an assumption regarding a population parameter. The methodology employed by the analyst depends on the nature of the data used ...
In hypothesis testing, the goal is to see if there is sufficient statistical evidence to reject a presumed null hypothesis in favor of a conjectured alternative hypothesis.The null hypothesis is usually denoted \(H_0\) while the alternative hypothesis is usually denoted \(H_1\). An hypothesis test is a statistical decision; the conclusion will either be to reject the null hypothesis in favor ...
A hypothesis test is a statistical inference method used to test the significance of a proposed (hypothesized) relation between population statistics (parameters) and their corresponding sample estimators. In other words, hypothesis tests are used to determine if there is enough evidence in a sample to prove a hypothesis true for the entire population. The test considers two hypotheses: the ...
Hypothesis testing is a crucial procedure to perform when you want to make inferences about a population using a random sample. These inferences include estimating population properties such as the mean, differences between means, proportions, and the relationships between variables. This post provides an overview of statistical hypothesis testing.
Unit test. Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values to make conclusions about hypotheses.
Hypothesis testing is based on making two different claims about a population parameter. The null hypothesis ( H 0) and the alternative hypothesis ( H 1) are the claims. The two claims needs to be mutually exclusive, meaning only one of them can be true. The alternative hypothesis is typically what we are trying to prove.
Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid. A null hypothesis and an alternative ...
HYPOTHESIS TESTING. A clinical trial begins with an assumption or belief, and then proceeds to either prove or disprove this assumption. In statistical terms, this belief or assumption is known as a hypothesis. Counterintuitively, what the researcher believes in (or is trying to prove) is called the "alternate" hypothesis, and the opposite ...
Defining Hypotheses. Null hypothesis (H 0): In statistics, the null hypothesis is a general statement or default position that there is no relationship between two measured cases or no relationship among groups. In other words, it is a basic assumption or made based on the problem knowledge. Example: A company's mean production is 50 units/per da H 0: [Tex]\mu [/Tex] = 50.
Statistical hypothesis testing is defined as: Assessing evidence provided by the data against the null claim (the claim which is to be assumed true unless enough evidence exists to reject it). ... doesn't mean the null hypothesis is necessarily true (so, we never "accept" the null); it only means that the particular study didn't yield ...
Statistics - Hypothesis Testing, Sampling, Analysis: Hypothesis testing is a form of statistical inference that uses data from a sample to draw conclusions about a population parameter or a population probability distribution. First, a tentative assumption is made about the parameter or distribution. This assumption is called the null hypothesis and is denoted by H0.
Definition: statistical procedure. Hypothesis testing is a statistical procedure in which a choice is made between a null hypothesis and an alternative hypothesis based on information in a sample. The end result of a hypotheses testing procedure is a choice of one of the following two possible conclusions: Reject H0.
Components of a Formal Hypothesis Test. The null hypothesis is a statement about the value of a population parameter, such as the population mean (µ) or the population proportion (p).It contains the condition of equality and is denoted as H 0 (H-naught).. H 0: µ = 157 or H0 : p = 0.37. The alternative hypothesis is the claim to be tested, the opposite of the null hypothesis.
Test statistics represent effect sizes in hypothesis tests because they denote the difference between your sample effect and no effect —the null hypothesis. Consequently, you use the test statistic to calculate the p-value for your hypothesis test. The above p-value definition is a bit tortuous.
A test is considered to be statistically significant when the p-value is less than or equal to the level of significance, also known as the alpha ( α) level. For this class, unless otherwise specified, α = 0.05; this is the most frequently used alpha level in many fields. Sample statistics vary from the population parameter randomly.
Below these are summarized into six such steps to conducting a test of a hypothesis. Set up the hypotheses and check conditions: Each hypothesis test includes two hypotheses about the population. One is the null hypothesis, notated as H 0, which is a statement of a particular parameter value. This hypothesis is assumed to be true until there is ...
ANOVA and MANOVA tests are used when comparing the means of more than two groups (e.g., the average heights of children, teenagers, and adults). Predictor variable. Outcome variable. Research question example. Paired t-test. Categorical. 1 predictor. Quantitative. groups come from the same population.
Step 7: Based on Steps 5 and 6, draw a conclusion about H 0. If F calculated is larger than F α, then you are in the rejection region and you can reject the null hypothesis with ( 1 − α) level of confidence. Note that modern statistical software condenses Steps 6 and 7 by providing a p -value. The p -value here is the probability of getting ...