- 1-224-725-3522
- [email protected]

Hypothesis Testing for a proportion Calculator

| Enter x (# of successes) | Enter n (sample size) | Enter H | Enter α |
|---|---|---|---|
| p |
How does the Hypothesis Testing for a proportion Calculator work?
What 2 formulas are used for the hypothesis testing for a proportion calculator, what 6 concepts are covered in the hypothesis testing for a proportion calculator.

An Automated Online Math Tutor serving 8.1 million parents and students in 235 countries and territories.

Our Services
- All Subjects
- A.I. Training Data and Analytics
- Get Paid as an Affiliate
Top Categories
- Trigonometry
- Pre-Algebra
- Pre-Calculus
- Post a Math Problem

Hypothesis Testing Calculator
| $H_o$: | |||
| $H_a$: | μ | ≠ | μ₀ |
| $n$ | = | $\bar{x}$ | = | = |
| $\text{Test Statistic: }$ | = |
| $\text{Degrees of Freedom: } $ | $df$ | = |
| $ \text{Level of Significance: } $ | $\alpha$ | = |
Type II Error
| $H_o$: | $\mu$ | ||
| $H_a$: | $\mu$ | ≠ | $\mu_0$ |
| $n$ | = | σ | = | $\mu$ | = |
| $\text{Level of Significance: }$ | $\alpha$ | = |
The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. To switch from σ known to σ unknown, click on $\boxed{\sigma}$ and select $\boxed{s}$ in the Hypothesis Testing Calculator.
| $\sigma$ Known | $\sigma$ Unknown | |
| Test Statistic | $ z = \dfrac{\bar{x}-\mu_0}{\sigma/\sqrt{{\color{Black} n}}} $ | $ t = \dfrac{\bar{x}-\mu_0}{s/\sqrt{n}} $ |
Next, the test statistic is used to conduct the test using either the p-value approach or critical value approach. The particular steps taken in each approach largely depend on the form of the hypothesis test: lower tail, upper tail or two-tailed. The form can easily be identified by looking at the alternative hypothesis (H a ). If there is a less than sign in the alternative hypothesis then it is a lower tail test, greater than sign is an upper tail test and inequality is a two-tailed test. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.
| Lower Tail Test | Upper Tail Test | Two-Tailed Test |
| $H_0 \colon \mu \geq \mu_0$ | $H_0 \colon \mu \leq \mu_0$ | $H_0 \colon \mu = \mu_0$ |
| $H_a \colon \mu | $H_a \colon \mu \neq \mu_0$ |
In the p-value approach, the test statistic is used to calculate a p-value. If the test is a lower tail test, the p-value is the probability of getting a value for the test statistic at least as small as the value from the sample. If the test is an upper tail test, the p-value is the probability of getting a value for the test statistic at least as large as the value from the sample. In a two-tailed test, the p-value is the probability of getting a value for the test statistic at least as unlikely as the value from the sample.
To test the hypothesis in the p-value approach, compare the p-value to the level of significance. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. If the p-value is greater than the level of significance, do not reject the null hypothesis. This method remains unchanged regardless of whether it's a lower tail, upper tail or two-tailed test. To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice.
In the critical value approach, the level of significance ($\alpha$) is used to calculate the critical value. In a lower tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the lower tail of the sampling distribution of the test statistic. In an upper tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the upper tail of the sampling distribution of the test statistic. In a two-tailed test, the critical values are the values of the test statistic providing areas of $\alpha / 2$ in the lower and upper tail of the sampling distribution of the test statistic.
To test the hypothesis in the critical value approach, compare the critical value to the test statistic. Unlike the p-value approach, the method we use to decide whether to reject the null hypothesis depends on the form of the hypothesis test. In a lower tail test, if the test statistic is less than or equal to the critical value, reject the null hypothesis. In an upper tail test, if the test statistic is greater than or equal to the critical value, reject the null hypothesis. In a two-tailed test, if the test statistic is less than or equal the lower critical value or greater than or equal to the upper critical value, reject the null hypothesis.
| Lower Tail Test | Upper Tail Test | Two-Tailed Test |
| If $z \leq -z_\alpha$, reject $H_0$. | If $z \geq z_\alpha$, reject $H_0$. | If $z \leq -z_{\alpha/2}$ or $z \geq z_{\alpha/2}$, reject $H_0$. |
| If $t \leq -t_\alpha$, reject $H_0$. | If $t \geq t_\alpha$, reject $H_0$. | If $t \leq -t_{\alpha/2}$ or $t \geq t_{\alpha/2}$, reject $H_0$. |
When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. There are two types of errors you can make: Type I Error and Type II Error. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true.
| Condition | ||||
| $H_0$ True | $H_a$ True | |||
| Conclusion | Accept $H_0$ | Correct | Type II Error | |
| Reject $H_0$ | Type I Error | Correct | ||
Hypothesis testing is closely related to the statistical area of confidence intervals. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Confidence intervals can be found using the Confidence Interval Calculator . The calculator on this page does hypothesis tests for one population mean. Sometimes we're interest in hypothesis tests about two population means. These can be solved using the Two Population Calculator . The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.
Other calculators ...
Free statistical calculators, test for one proportion calculator.
| : | |
|---|---|
| : | |
| : | |
Description
The Test for one proportion can be used to test the hypothesis that an observed proportion is equal to a pre-specified proportion.
This test is not performed on data in the data table, but on statistics you enter in a dialog box.
Required input
Computational notes.
The significance level, or P-value, is calculated using a general z-test (Altman, 1991):
where p is the observed proportion; p exp is the Null hypothesis (or expected) proportion; and se ( p ) is the standard error of the expected proportion:

The P-value is the area of the normal distribution that falls outside ± z (see Values of the Normal distribution table).
If the P-value is less than 0.05, the hypothesis that the observed proportion is equal to the pre-specified proportion value is rejected, and the alternative hypothesis that there is a significant difference between the two proportions can be accepted.
Confidence interval
MedCalc calculates the "exact" Clopper-Pearson confidence interval for the observed proportion (Clopper & Pearson, 1934; Fleis et al., 2003).
How to cite this page
This calculator runs a one sample proportion test for a given sample data set and specified null and alternative hypotheses. In the fields below enter the sample size \(n\) and the number of scores with the trait of interest, \(f\).
Enter a value for the null hypothesis. This value should indicate the absence of an effect in your data. It must be between the values 0 and 1. Indicate whether your alternative hypothesis involves one-tail or two-tails. If it is a one-tailed test, then you need to indicate whether it is a positive (right tail) test or a negative (left tail) test.
Enter an \(\alpha\) value for the hypothesis test. This is the Type I error rate for your hypothesis test. It also determines the confidence level \(100 \times (1-\alpha)\) for a confidence interval. The confidence interval is based on the normal distribution, which is an approximation.
Press the Run Test button and a table summarizing the computations and conclusions will appear below.
| Specify hypotheses: | |||
|---|---|---|---|
| \(H_0: P=\) |
| \(H_a:\) |
| \(\alpha=\) |
| Test summary | ||
|---|---|---|
| Null hypothesis | \(H_0: P=\) | |
| Alternative hypothesis | \(H_a: P \) | |
| Type I error rate | \(\alpha=\) | |
| Sample size | \(n=\) | |
| Sample proportion | \(p=\) | |
| Sample standard error | \(s_p=\) | |
| Test statistic | \(z=\) | |
| \(p\) value | \(p=\) | |
| Decision | ||
| Confidence interval critical value | \(z_{cv}=\) | |
| Confidence interval standard error | \(s_p=\) | |
| Confidence interval | CI = | |
Proportion Test
One sample proportion test (go to the calculator), assumptions, required sample data, test statistic.
| x | p(X=x) | p(X≤x) | p(X≥x) |
|---|---|---|---|
| 0 | 0.100112915 | 0.100112915 | 1 |
| 1 | 0.266967773 | 0.367080688 | 0.899887085 |
| 2 | 0.311462402 | 0.678543091 | 0.632919312 |
| 3 | 0.207641602 | 0.886184692 | 0.321456909 |
| 4 | 0.086517334 | 0.972702026 | 0.113815308 |
| 5 | 0.023071289 | 0.995773315 | 0.027297974 |
| 6 | 0.003845215 | 0.99961853 | 0.004226685 |
| 7 | 0.000366211 | 0.999984741 | 0.00038147 |
| 8 | 1.52588E-05 | 1 | 1.52588E-05 |
Effect size
The tool calculates the h effect size . $$\varphi(p)=2arcsine(\sqrt{p})\\ h=\varphi(p̂)-\varphi(P_0)$$ Cohen's interpretation for the h effect size: Small effect - 0.2. Medium effect - 0.5. Large effect - 0.8.
Two Sample proportion test (Go to the calculator)
This calculator runs a two sample independent proportions test for given sample data and specified null and alternative hypotheses. Enter the data in the fields below. For each sample enter the total number of scores (\(n_1\) and \(n_2\)) and the number of scores that have the trait of interest (\(f_1\) and \(f_2\)).
Enter a value for the null hypothesis. This value should indicate the absence of an effect in your data. It must be between the values 0 and 1. Indicate whether your alternative hypothesis involves one-tail or two-tails. If it is a one-tailed test, then you need to indicate whether it is a positive (right tail) test or a negative (left tail) test.
Enter an \(\alpha\) value for the hypothesis test. This is the Type I error rate for your hypothesis test. It also determines the confidence level \(100 \times (1-\alpha)\) for a confidence interval. The confidence interval is based on the normal distribution, which is an approximation.
Press the Run Test button and a table summarizing the computations and conclusions will appear below.
| Specify hypotheses: |
|---|
| \(H_0: P_1 - P_2=\) |
| \(H_a:\) |
| \(\alpha=\) |
| Test summary | ||
|---|---|---|
| Null hypothesis | \(H_0: P_1 - P_2=\) | |
| Alternative hypothesis | \(H_a: P_1 - P_2 \) | |
| Type I error rate | \(\alpha=\) | |
| Sample size for group 1 | \(n_1=\) | |
| Sample size for group 2 | \(n_2=\) | |
| Sample proportion for group 1 | \(p_1=\) | |
| Sample proportion for group 2 | \(p_2=\) | |
| Pooled proportion | \(p=\) | |
| Standard error | \(s_{p_1 - p_2}=\) | |
| Test statistic | \(z=\) | |
| \(p\) value | \(p=\) | |
| Decision | ||
| Confidence interval critical value | \(z_{cv}=\) | |
| Confidence interval | CI = | |

- Calculators
- Descriptive Statistics
- Merchandise
- Which Statistics Test?
Z Score Calculator for 2 Population Proportions
This is a simple z score calculator that calculates the value of z (and associated p value) for two population proportions.
Further Information
The z score test for two population proportions is used when you want to know whether two populations or groups (e.g., males and females; theists and atheists) differ significantly on some single (categorical) characteristic - for example, whether they are vegetarians.
Requirements
- A random sample of each of the population groups to be compared.
- Categorial data
Null Hypothesis
H0: p1 - p2 = 0, where p1 is the proportion from the first population and p2 the proportion from the second.
As above, the null hypothesis tends to be that there is no difference between the two population proportions; or, more formally, that the difference is zero (so, for example, that there is no difference between the proportion of males who are vegetarian and the proportion of females who are vegetarian).

Z-test for Two Proportions
Instructions: This calculator conducts a Z-test for two population proportions (\(p_1\) and \(p_2\)), Please select the null and alternative hypotheses, type the significance level, the sample sizes, the number of favorable cases (or the sample proportions) and the results of the z-test will be displayed for you:

When Do You Use a Z-test for Two Proportions?
More about the z-test for two proportions so you can better understand the results yielded by this solver: A z-test for two proportions is a hypothesis test that attempts to make a claim about the population proportions p 1 and p 2 . Specifically, we are interested in assessing whether or not it is reasonable to claim that p 1 = p 2 , using sample information. The Z-test for two proportions has two non-overlapping hypotheses, the null and the alternative hypothesis.
What are the null and alternative hypotheses for the z-test for two proportions?
The null hypothesis is a statement about the population parameter which indicates no effect, and the alternative hypothesis is the complementary hypothesis to the null hypothesis. The main properties of a one sample z-test for two population proportions are:
- Depending on our knowledge about the "no effect" situation, the z-test can be two-tailed, left-tailed or right-tailed
- The main principle of hypothesis testing is that the null hypothesis is rejected if the test statistic obtained is sufficiently unlikely under the assumption that the null hypothesis is true
- The p-value is the probability of obtaining sample results as extreme or more extreme than the sample results obtained, under the assumption that the null hypothesis is true
- In a hypothesis tests there are two types of errors. Type I error occurs when we reject a true null hypothesis, and the Type II error occurs when we fail to reject a false null hypothesis
What is the z-test formula in this case?
The formula for a z-statistic for two population proportions is
where \(\bar p = \frac{X_1+X_2}{n_1+n_2}\) corresponds to the pooled proportion (Notice that in the above z test for proportions formula, we get in the denominator something like our "best guess" of what the population proportion is from information from the two samples, assuming that the null hypothesis of equality of proportions is true). The null hypothesis is rejected when the z-statistic lies on the rejection region, which is determined by the significance level (\(\alpha\)) and the type of tail (two-tailed, left-tailed or right-tailed).
The Case for one population proportion
In case you only have one sample proportion (so you are testing for one population proportion), you should use our z-test for one proportion calculator , which specifically addresses that case.
Related Calculators

log in to your account
Reset password.
Informative
Conversion Calculator
Follow Us On:
Test Statistic Calculator
Choose the method, enter the values into the test statistic calculator, and click on the “Calculate” button to calculate the statistical value for hypothesis evaluation.
Add this calculator to your site
This test statistic calculator helps to find the static value for hypothesis testing. The calculated test value shows if there’s enough evidence to reject a null hypothesis. Also, this calculator performs calculations of either for one population mean, comparing two means, single population proportion, and two population proportions.
Our tool is highly useful in various fields like research, experimentation, quality control, and data analysis.
What is Test Statistics?
A test statistic is a numerical value obtained from the sample data set. It summarizes the differences between what you observe within your sample and what would be expected if a hypothesis were true.
The t-test statistic also shows how closely your data matches the predicted distribution among the sample tests you perform.
How to Calculate Test Statistics Value?
- Collect the data from the populations
- Use the data to find the standard deviation of the population
- Calculate the mean (μ) of the population using this data
- Determine the z-value or sample size
- Use the suitable test statistic formula and get the results
Test Statistic For One Population Mean:
Test statistics for a single population mean is calculated when a variable is numeric and involves one population or a group.
x̄ - µ 0 σ / √n
- x̄ = Mean of your sample data
- µ 0 = Hypothesized population mean that you are comparing to your sample mean
- σ = Population standard deviation
- n = number of observations (sample size) in your data set
Suppose we want to test if the average height of adult males in a city is 70 inches. We take a sample of 25 adult males and find the sample mean height to be 71 inches with a sample standard deviation of 3 inches. We use a significance level of 0.05.
t = 70 - 71 3√25
Test Statistic Comparing Two Population Means:
This test is applied when the numeric value is compared across the various populations or groups. To compute the resulting t statistic, two distinct random samples must be chosen, one from each population.
\(\frac{√x̄ - √ȳ}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\)
- ȳ = means of hypothesized population
Suppose we want to test if there is a difference in average test scores between two schools. We take a sample of 30 students from school A with an average score of 85 and a standard deviation of 5, and a sample of 35 students from school B with an average score of 82 and a standard deviation of 6.
t = 85 - 82 √5 2 / 30 + 6 2 / 35
t = 3 √ 25/30 + 36/35
t = 3 √0.833 + 1.029
t = 3 √1.862
Test Statistic For a Single Population Proportion:
This test is used to determine if a single population's proportion differs from a specified standard. The t statistic calculator works for a population proportion when dealing with data by having a limit of P₀ because proportions represent parts of a whole and cannot logically exceed the total or be negative.
\(\frac{\hat{p}-p_{0}}{\sqrt{\frac{p_{0}(1-p_{0})}{n}}}\)
- P̂ = Sample proportion
- P 0 = Population proportion
Suppose we want to test if the proportion of left-handed people in a population is 10%. We take a sample of 100 people and find that 8 are left-handed. We use a significance level of 0.05.
= P̂ - P₀ √0.10 (1 - 0.10)/100
= 0.08 - 0.10 √0.10 (1 - 0.10)/100
= -0.02 √0.10 (0.9)/100
= -0.02 √0.009
= -0.02 0.03
= −0.67
Test Statistic For Two Population Proportion:
This test identifies the difference in proportions between two independent groups to assess their significance.
\(\frac{\hat{p}_{1}-\hat{p}_{2}}{\sqrt{\hat{p}(1-\hat{p})(\frac{1}{n_{1}}+\frac{1}{n_{2}})}}\)
- P̂ 1 and P̂ 2 = Sample proportions for two groups
Suppose we want to test if the proportion of smokers is different between two cities. We take a sample of 150 people from City A and find that 30 are smokers, and a sample of 200 people from City B and find that 50 are smokers.
- P̂ 1 = 30 / 150 = 0.20
- P̂ 2 = 50 / 200 = 0.25
- P̂ = 30 + 50 / 150 + 200 = 0.229
Calculation:
= 0.20 - 0.25 √0.229 (1 - 0.229) (1 / 150 + 1/200)
= -0.05 √0.229 (0.771) (1 / 150 + 1 / 200)
= -0.05 √0.176 (1/150 + 1/200)
= -0.05 √0.176 (0.0113)
= -0.05 √0.002
= -0.05 0.045
= −1.11
Sample Distribution Calculator
Sample Size Calculator
Effect Size Calculator
Chi-Square Calculator
Critical Value Calculator
Probability Calculator
Pie Chart Calculator
Add this calculator to your site.
Just copy a given code & paste it right now into your website HTML (source) for suitable page.
Give Us Your Feedback
Share Result

Get the ease of calculating anything from the source of calculator online
Email us at
© Copyrights 2024 by Calculator-Online.net
P-value Calculator
Statistical significance calculator to easily calculate the p-value and determine whether the difference between two proportions or means (independent groups) is statistically significant. T-test calculator & z-test calculator to compute the Z-score or T-score for inference about absolute or relative difference (percentage change, percent effect). Suitable for analysis of simple A/B tests.
Related calculators
- Using the p-value calculator
- What is "p-value" and "significance level"
- P-value formula
- Why do we need a p-value?
- How to interpret a statistically significant result / low p-value
- P-value and significance for relative difference in means or proportions
Using the p-value calculator
This statistical significance calculator allows you to perform a post-hoc statistical evaluation of a set of data when the outcome of interest is difference of two proportions (binomial data, e.g. conversion rate or event rate) or difference of two means (continuous data, e.g. height, weight, speed, time, revenue, etc.). You can use a Z-test (recommended) or a T-test to find the observed significance level (p-value statistic). The Student's T-test is recommended mostly for very small sample sizes, e.g. n < 30. In order to avoid type I error inflation which might occur with unequal variances the calculator automatically applies the Welch's T-test instead of Student's T-test if the sample sizes differ significantly or if one of them is less than 30 and the sampling ratio is different than one.
If entering proportions data, you need to know the sample sizes of the two groups as well as the number or rate of events. These can be entered as proportions (e.g. 0.10), percentages (e.g. 10%) or just raw numbers of events (e.g. 50).
If entering means data, simply copy/paste or type in the raw data, each observation separated by comma, space, new line or tab. Copy-pasting from a Google or Excel spreadsheet works fine.
The p-value calculator will output : p-value, significance level, T-score or Z-score (depending on the choice of statistical hypothesis test), degrees of freedom, and the observed difference. For means data it will also output the sample sizes, means, and pooled standard error of the mean. The p-value is for a one-sided hypothesis (one-tailed test), allowing you to infer the direction of the effect (more on one vs. two-tailed tests ). However, the probability value for the two-sided hypothesis (two-tailed p-value) is also calculated and displayed, although it should see little to no practical applications.
Warning: You must have fixed the sample size / stopping time of your experiment in advance, otherwise you will be guilty of optional stopping (fishing for significance) which will inflate the type I error of the test rendering the statistical significance level unusable. Also, you should not use this significance calculator for comparisons of more than two means or proportions, or for comparisons of two groups based on more than one metric. If a test involves more than one treatment group or more than one outcome variable you need a more advanced tool which corrects for multiple comparisons and multiple testing. This statistical calculator might help.
What is "p-value" and "significance level"
The p-value is a heavily used test statistic that quantifies the uncertainty of a given measurement, usually as a part of an experiment, medical trial, as well as in observational studies. By definition, it is inseparable from inference through a Null-Hypothesis Statistical Test (NHST) . In it we pose a null hypothesis reflecting the currently established theory or a model of the world we don't want to dismiss without solid evidence (the tested hypothesis), and an alternative hypothesis: an alternative model of the world. For example, the statistical null hypothesis could be that exposure to ultraviolet light for prolonged periods of time has positive or neutral effects regarding developing skin cancer, while the alternative hypothesis can be that it has a negative effect on development of skin cancer.
In this framework a p-value is defined as the probability of observing the result which was observed, or a more extreme one, assuming the null hypothesis is true . In notation this is expressed as:
p(x 0 ) = Pr(d(X) > d(x 0 ); H 0 )
where x 0 is the observed data (x 1 ,x 2 ...x n ), d is a special function (statistic, e.g. calculating a Z-score), X is a random sample (X 1 ,X 2 ...X n ) from the sampling distribution of the null hypothesis. This equation is used in this p-value calculator and can be visualized as such:

Therefore the p-value expresses the probability of committing a type I error : rejecting the null hypothesis if it is in fact true. See below for a full proper interpretation of the p-value statistic .
Another way to think of the p-value is as a more user-friendly expression of how many standard deviations away from the normal a given observation is. For example, in a one-tailed test of significance for a normally-distributed variable like the difference of two means, a result which is 1.6448 standard deviations away (1.6448σ) results in a p-value of 0.05.
The term "statistical significance" or "significance level" is often used in conjunction to the p-value, either to say that a result is "statistically significant", which has a specific meaning in statistical inference ( see interpretation below ), or to refer to the percentage representation the level of significance: (1 - p value), e.g. a p-value of 0.05 is equivalent to significance level of 95% (1 - 0.05 * 100). A significance level can also be expressed as a T-score or Z-score, e.g. a result would be considered significant only if the Z-score is in the critical region above 1.96 (equivalent to a p-value of 0.025).
P-value formula
There are different ways to arrive at a p-value depending on the assumption about the underlying distribution. This tool supports two such distributions: the Student's T-distribution and the normal Z-distribution (Gaussian) resulting in a T test and a Z test, respectively.
In both cases, to find the p-value start by estimating the variance and standard deviation, then derive the standard error of the mean, after which a standard score is found using the formula [2] :
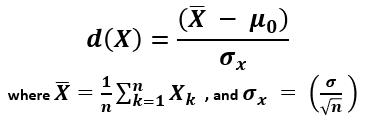
X (read "X bar") is the arithmetic mean of the population baseline or the control, μ 0 is the observed mean / treatment group mean, while σ x is the standard error of the mean (SEM, or standard deviation of the error of the mean).
When calculating a p-value using the Z-distribution the formula is Φ(Z) or Φ(-Z) for lower and upper-tailed tests, respectively. Φ is the standard normal cumulative distribution function and a Z-score is computed. In this mode the tool functions as a Z score calculator.
When using the T-distribution the formula is T n (Z) or T n (-Z) for lower and upper-tailed tests, respectively. T n is the cumulative distribution function for a T-distribution with n degrees of freedom and so a T-score is computed. Selecting this mode makes the tool behave as a T test calculator.
The population standard deviation is often unknown and is thus estimated from the samples, usually from the pooled samples variance. Knowing or estimating the standard deviation is a prerequisite for using a significance calculator. Note that differences in means or proportions are normally distributed according to the Central Limit Theorem (CLT) hence a Z-score is the relevant statistic for such a test.
Why do we need a p-value?
If you are in the sciences, it is often a requirement by scientific journals. If you apply in business experiments (e.g. A/B testing) it is reported alongside confidence intervals and other estimates. However, what is the utility of p-values and by extension that of significance levels?
First, let us define the problem the p-value is intended to solve. People need to share information about the evidential strength of data that can be easily understood and easily compared between experiments. The picture below represents, albeit imperfectly, the results of two simple experiments, each ending up with the control with 10% event rate treatment group at 12% event rate.
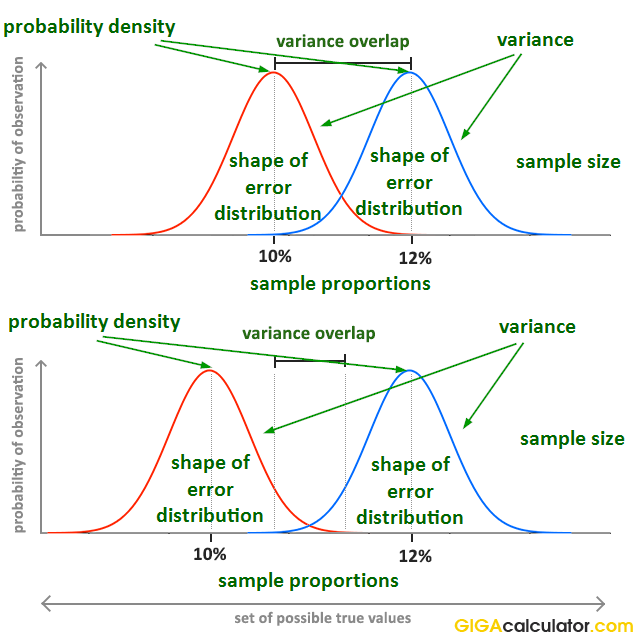
However, it is obvious that the evidential input of the data is not the same, demonstrating that communicating just the observed proportions or their difference (effect size) is not enough to estimate and communicate the evidential strength of the experiment. In order to fully describe the evidence and associated uncertainty , several statistics need to be communicated, for example, the sample size, sample proportions and the shape of the error distribution. Their interaction is not trivial to understand, so communicating them separately makes it very difficult for one to grasp what information is present in the data. What would you infer if told that the observed proportions are 0.1 and 0.12 (e.g. conversion rate of 10% and 12%), the sample sizes are 10,000 users each, and the error distribution is binomial?
Instead of communicating several statistics, a single statistic was developed that communicates all the necessary information in one piece: the p-value . A p-value was first derived in the late 18-th century by Pierre-Simon Laplace, when he observed data about a million births that showed an excess of boys, compared to girls. Using the calculation of significance he argued that the effect was real but unexplained at the time. We know this now to be true and there are several explanations for the phenomena coming from evolutionary biology. Statistical significance calculations were formally introduced in the early 20-th century by Pearson and popularized by Sir Ronald Fisher in his work, most notably "The Design of Experiments" (1935) [1] in which p-values were featured extensively. In business settings significance levels and p-values see widespread use in process control and various business experiments (such as online A/B tests, i.e. as part of conversion rate optimization, marketing optimization, etc.).
How to interpret a statistically significant result / low p-value
Saying that a result is statistically significant means that the p-value is below the evidential threshold (significance level) decided for the statistical test before it was conducted. For example, if observing something which would only happen 1 out of 20 times if the null hypothesis is true is considered sufficient evidence to reject the null hypothesis, the threshold will be 0.05. In such case, observing a p-value of 0.025 would mean that the result is interpreted as statistically significant.
But what does that really mean? What inference can we make from seeing a result which was quite improbable if the null was true?
Observing any given low p-value can mean one of three things [3] :
- There is a true effect from the tested treatment or intervention.
- There is no true effect, but we happened to observe a rare outcome. The lower the p-value, the rarer (less likely, less probable) the outcome.
- The statistical model is invalid (does not reflect reality).
Obviously, one can't simply jump to conclusion 1.) and claim it with one hundred percent certainty, as this would go against the whole idea of the p-value and statistical significance. In order to use p-values as a part of a decision process external factors part of the experimental design process need to be considered which includes deciding on the significance level (threshold), sample size and power (power analysis), and the expected effect size, among other things. If you are happy going forward with this much (or this little) uncertainty as is indicated by the p-value calculation suggests, then you have some quantifiable guarantees related to the effect and future performance of whatever you are testing, e.g. the efficacy of a vaccine or the conversion rate of an online shopping cart.
Note that it is incorrect to state that a Z-score or a p-value obtained from any statistical significance calculator tells how likely it is that the observation is "due to chance" or conversely - how unlikely it is to observe such an outcome due to "chance alone". P-values are calculated under specified statistical models hence 'chance' can be used only in reference to that specific data generating mechanism and has a technical meaning quite different from the colloquial one. For a deeper take on the p-value meaning and interpretation, including common misinterpretations, see: definition and interpretation of the p-value in statistics .
P-value and significance for relative difference in means or proportions
When comparing two independent groups and the variable of interest is the relative (a.k.a. relative change, relative difference, percent change, percentage difference), as opposed to the absolute difference between the two means or proportions, the standard deviation of the variable is different which compels a different way of calculating p-values [5] . The need for a different statistical test is due to the fact that in calculating relative difference involves performing an additional division by a random variable: the event rate of the control during the experiment which adds more variance to the estimation and the resulting statistical significance is usually higher (the result will be less statistically significant). What this means is that p-values from a statistical hypothesis test for absolute difference in means would nominally meet the significance level, but they will be inadequate given the statistical inference for the hypothesis at hand.
In simulations I performed the difference in p-values was about 50% of nominal: a 0.05 p-value for absolute difference corresponded to probability of about 0.075 of observing the relative difference corresponding to the observed absolute difference. Therefore, if you are using p-values calculated for absolute difference when making an inference about percentage difference, you are likely reporting error rates which are about 50% of the actual, thus significantly overstating the statistical significance of your results and underestimating the uncertainty attached to them.
In short - switching from absolute to relative difference requires a different statistical hypothesis test. With this calculator you can avoid the mistake of using the wrong test simply by indicating the inference you want to make.
References
1 Fisher R.A. (1935) – "The Design of Experiments", Edinburgh: Oliver & Boyd
2 Mayo D.G., Spanos A. (2010) – "Error Statistics", in P. S. Bandyopadhyay & M. R. Forster (Eds.), Philosophy of Statistics, (7, 152–198). Handbook of the Philosophy of Science . The Netherlands: Elsevier.
3 Georgiev G.Z. (2017) "Statistical Significance in A/B Testing – a Complete Guide", [online] https://blog.analytics-toolkit.com/2017/statistical-significance-ab-testing-complete-guide/ (accessed Apr 27, 2018)
4 Mayo D.G., Spanos A. (2006) – "Severe Testing as a Basic Concept in a Neyman–Pearson Philosophy of Induction", British Society for the Philosophy of Science , 57:323-357
5 Georgiev G.Z. (2018) "Confidence Intervals & P-values for Percent Change / Relative Difference", [online] https://blog.analytics-toolkit.com/2018/confidence-intervals-p-values-percent-change-relative-difference/ (accessed May 20, 2018)
Cite this calculator & page
If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation: Georgiev G.Z., "P-value Calculator" , [online] Available at: https://www.gigacalculator.com/calculators/p-value-significance-calculator.php URL [Accessed Date: 11 Aug, 2024].
Our statistical calculators have been featured in scientific papers and articles published in high-profile science journals by:

The author of this tool

Statistical calculators
Teach yourself statistics
Hypothesis Test for a Proportion
This lesson explains how to conduct a hypothesis test of a proportion, when the following conditions are met:
- The sampling method is simple random sampling .
- Each sample point can result in just two possible outcomes. We call one of these outcomes a success and the other, a failure.
- The sample includes at least 10 successes and 10 failures.
- The population size is at least 20 times as big as the sample size.
This approach consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.
State the Hypotheses
Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis . The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.
Formulate an Analysis Plan
The analysis plan describes how to use sample data to accept or reject the null hypothesis. It should specify the following elements.
- Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
- Test method. Use the one-sample z-test to determine whether the hypothesized population proportion differs significantly from the observed sample proportion.

Analyze Sample Data
Using sample data, find the test statistic and its associated P-Value.
σ = sqrt[ P * ( 1 - P ) / n ]
z = (p - P) / σ
- P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a z-score, use the Normal Distribution Calculator to assess the probability associated with the z-score. (See sample problems at the end of this lesson for examples of how this is done.)
Interpret Results
If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.
Test Your Understanding
In this section, two hypothesis testing examples illustrate how to conduct a hypothesis test of a proportion. The first problem involves a a two-tailed test; the second problem, a one-tailed test.
Sample Size Calculator
As you probably noticed, the process of testing a hypothesis about a proportion can be complex. Stat Trek's Sample Size Calculator can do the same job quickly and easily. When you need to test a hypothesis, consider using the Sample Size Calculator. The calculator is free. It can found in the Stat Trek main menu under the Stat Tools tab. Or you can tap the button below.
Problem 1: Two-Tailed Test
The CEO of a large electric utility claims that 80 percent of his 1,000,000 customers are very satisfied with the service they receive. To test this claim, the local newspaper surveyed 100 customers, using simple random sampling. Among the sampled customers, 73 percent say they are very satisified. Based on these findings, can we reject the CEO's hypothesis that 80% of the customers are very satisfied? Use a 0.05 level of significance.
Solution: The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:
State the hypotheses. The first step is to state the null hypothesis and an alternative hypothesis.
Null hypothesis: P = 0.80
Alternative hypothesis: P ≠ 0.80
- Formulate an analysis plan . For this analysis, the significance level is 0.05. The test method, shown in the next section, is a one-sample z-test .
σ = sqrt [(0.8 * 0.2) / 100]
σ = sqrt(0.0016) = 0.04
z = (p - P) / σ = (.73 - .80)/0.04 = -1.75
where P is the hypothesized value of population proportion in the null hypothesis, p is the sample proportion, and n is the sample size.
Since we have a two-tailed test , the P-value is the probability that the z-score is less than -1.75 or greater than 1.75. We use the Normal Distribution Calculator to find P(z < -1.75) = 0.04. Since the standard normal distribution is symmetric with a mean of zero, we know that P(z > 1.75) = 0.04. Thus, the P-value = 0.04 + 0.04 = 0.08.
- Interpret results . Since the P-value (0.08) is greater than the significance level (0.05), we cannot reject the null hypothesis.
Note: If you use this approach on an exam, you may also want to mention why this approach is appropriate. Specifically, the approach is appropriate because the sampling method was simple random sampling, the sample included at least 10 successes and 10 failures, and the population size was at least 10 times the sample size.
Problem 2: One-Tailed Test Suppose the previous example is stated a little bit differently. Suppose the CEO claims that at least 80 percent of the company's 1,000,000 customers are very satisfied. Again, 100 customers are surveyed using simple random sampling. The result: 73 percent are very satisfied. Based on these results, should we accept or reject the CEO's hypothesis? Assume a significance level of 0.05.
Null hypothesis: P >= 0.80
Alternative hypothesis: P < 0.80
σ = sqrt[ P * ( 1 - P ) / n ] = sqrt [(0.8 * 0.2) / 100]
- Interpret results . Since the P-value (0.04) is less than the significance level (0.05), we cannot accept the null hypothesis.
Enter a value for the null hypothesis. This value should indicate the absence of an effect in your data. Since the test is for a difference of proportions it must be between the values \(-1\) and \(+1\). Indicate whether your alternative hypothesis involves one-tail or two-tails. If it is a one-tailed test, then you need to indicate whether it is a positive (right tail) test or a negative (left tail) test.
Enter an \(\alpha\) value for the hypothesis test. This is the Type I error rate for your hypothesis test. It also determines the confidence level \(100 \times (1-\alpha)\) for a confidence interval.
Press the Run Test button and a table summarizing the computations and conclusions will appear below.
| Has Trait 2? | |||
| No | Yes | ||
| Has Trait 1? | Yes | \(A=\) | \(B=\) |
| No | \(C=\) | \(D=\) | |
| \(H_0: P_1 - P_2 =\) |
| \(H_a:\) |
| \(\alpha=\) |
| Test summary | ||
|---|---|---|
| Null hypothesis | \(H_0: P_1 - P_2=\) | |
| Alternative hypothesis | \(H_a: P_1 - P_2 \) | |
| Type I error rate | \(\alpha=\) | |
| Sample size | \(n=\) | |
| Sample proportion for group 1 | \(p_1=\) | |
| Sample proportion for group 2 | \(p_2=\) | |
| Disagreement proportion | \(p_d=\) | |
| Standard error | \(s_{p_1 - p_2}=\) | |
| Test statistic | \(z=\) | |
| \(p\) value | \(p=\) | |
| Decision | ||
| Confidence interval critical value | \(z_{cv}=\) | |
| Confidence interval | CI = | |
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Null Hypothesis: Definition, Rejecting & Examples
By Jim Frost 6 Comments
What is a Null Hypothesis?
The null hypothesis in statistics states that there is no difference between groups or no relationship between variables. It is one of two mutually exclusive hypotheses about a population in a hypothesis test.

- Null Hypothesis H 0 : No effect exists in the population.
- Alternative Hypothesis H A : The effect exists in the population.
In every study or experiment, researchers assess an effect or relationship. This effect can be the effectiveness of a new drug, building material, or other intervention that has benefits. There is a benefit or connection that the researchers hope to identify. Unfortunately, no effect may exist. In statistics, we call this lack of an effect the null hypothesis. Researchers assume that this notion of no effect is correct until they have enough evidence to suggest otherwise, similar to how a trial presumes innocence.
In this context, the analysts don’t necessarily believe the null hypothesis is correct. In fact, they typically want to reject it because that leads to more exciting finds about an effect or relationship. The new vaccine works!
You can think of it as the default theory that requires sufficiently strong evidence to reject. Like a prosecutor, researchers must collect sufficient evidence to overturn the presumption of no effect. Investigators must work hard to set up a study and a data collection system to obtain evidence that can reject the null hypothesis.
Related post : What is an Effect in Statistics?
Null Hypothesis Examples
Null hypotheses start as research questions that the investigator rephrases as a statement indicating there is no effect or relationship.
| Does the vaccine prevent infections? | The vaccine does not affect the infection rate. |
| Does the new additive increase product strength? | The additive does not affect mean product strength. |
| Does the exercise intervention increase bone mineral density? | The intervention does not affect bone mineral density. |
| As screen time increases, does test performance decrease? | There is no relationship between screen time and test performance. |
After reading these examples, you might think they’re a bit boring and pointless. However, the key is to remember that the null hypothesis defines the condition that the researchers need to discredit before suggesting an effect exists.
Let’s see how you reject the null hypothesis and get to those more exciting findings!
When to Reject the Null Hypothesis
So, you want to reject the null hypothesis, but how and when can you do that? To start, you’ll need to perform a statistical test on your data. The following is an overview of performing a study that uses a hypothesis test.
The first step is to devise a research question and the appropriate null hypothesis. After that, the investigators need to formulate an experimental design and data collection procedures that will allow them to gather data that can answer the research question. Then they collect the data. For more information about designing a scientific study that uses statistics, read my post 5 Steps for Conducting Studies with Statistics .
After data collection is complete, statistics and hypothesis testing enter the picture. Hypothesis testing takes your sample data and evaluates how consistent they are with the null hypothesis. The p-value is a crucial part of the statistical results because it quantifies how strongly the sample data contradict the null hypothesis.
When the sample data provide sufficient evidence, you can reject the null hypothesis. In a hypothesis test, this process involves comparing the p-value to your significance level .
Rejecting the Null Hypothesis
Reject the null hypothesis when the p-value is less than or equal to your significance level. Your sample data favor the alternative hypothesis, which suggests that the effect exists in the population. For a mnemonic device, remember—when the p-value is low, the null must go!
When you can reject the null hypothesis, your results are statistically significant. Learn more about Statistical Significance: Definition & Meaning .
Failing to Reject the Null Hypothesis
Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis. The sample data provides insufficient data to conclude that the effect exists in the population. When the p-value is high, the null must fly!
Note that failing to reject the null is not the same as proving it. For more information about the difference, read my post about Failing to Reject the Null .
That’s a very general look at the process. But I hope you can see how the path to more exciting findings depends on being able to rule out the less exciting null hypothesis that states there’s nothing to see here!
Let’s move on to learning how to write the null hypothesis for different types of effects, relationships, and tests.
Related posts : How Hypothesis Tests Work and Interpreting P-values
How to Write a Null Hypothesis
The null hypothesis varies by the type of statistic and hypothesis test. Remember that inferential statistics use samples to draw conclusions about populations. Consequently, when you write a null hypothesis, it must make a claim about the relevant population parameter . Further, that claim usually indicates that the effect does not exist in the population. Below are typical examples of writing a null hypothesis for various parameters and hypothesis tests.
Related posts : Descriptive vs. Inferential Statistics and Populations, Parameters, and Samples in Inferential Statistics
Group Means
T-tests and ANOVA assess the differences between group means. For these tests, the null hypothesis states that there is no difference between group means in the population. In other words, the experimental conditions that define the groups do not affect the mean outcome. Mu (µ) is the population parameter for the mean, and you’ll need to include it in the statement for this type of study.
For example, an experiment compares the mean bone density changes for a new osteoporosis medication. The control group does not receive the medicine, while the treatment group does. The null states that the mean bone density changes for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group means are equal in the population: µ 1 = µ 2 , or µ 1 – µ 2 = 0
- Alternative Hypothesis H A : Group means are not equal in the population: µ 1 ≠ µ 2 , or µ 1 – µ 2 ≠ 0.
Group Proportions
Proportions tests assess the differences between group proportions. For these tests, the null hypothesis states that there is no difference between group proportions. Again, the experimental conditions did not affect the proportion of events in the groups. P is the population proportion parameter that you’ll need to include.
For example, a vaccine experiment compares the infection rate in the treatment group to the control group. The treatment group receives the vaccine, while the control group does not. The null states that the infection rates for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group proportions are equal in the population: p 1 = p 2 .
- Alternative Hypothesis H A : Group proportions are not equal in the population: p 1 ≠ p 2 .
Correlation and Regression Coefficients
Some studies assess the relationship between two continuous variables rather than differences between groups.
In these studies, analysts often use either correlation or regression analysis . For these tests, the null states that there is no relationship between the variables. Specifically, it says that the correlation or regression coefficient is zero. As one variable increases, there is no tendency for the other variable to increase or decrease. Rho (ρ) is the population correlation parameter and beta (β) is the regression coefficient parameter.
For example, a study assesses the relationship between screen time and test performance. The null states that there is no correlation between this pair of variables. As screen time increases, test performance does not tend to increase or decrease.
- Null Hypothesis H 0 : The correlation in the population is zero: ρ = 0.
- Alternative Hypothesis H A : The correlation in the population is not zero: ρ ≠ 0.
For all these cases, the analysts define the hypotheses before the study. After collecting the data, they perform a hypothesis test to determine whether they can reject the null hypothesis.
The preceding examples are all for two-tailed hypothesis tests. To learn about one-tailed tests and how to write a null hypothesis for them, read my post One-Tailed vs. Two-Tailed Tests .
Related post : Understanding Correlation
Neyman, J; Pearson, E. S. (January 1, 1933). On the Problem of the most Efficient Tests of Statistical Hypotheses . Philosophical Transactions of the Royal Society A . 231 (694–706): 289–337.
Share this:

Reader Interactions
January 11, 2024 at 2:57 pm
Thanks for the reply.
January 10, 2024 at 1:23 pm
Hi Jim, In your comment you state that equivalence test null and alternate hypotheses are reversed. For hypothesis tests of data fits to a probability distribution, the null hypothesis is that the probability distribution fits the data. Is this correct?
January 10, 2024 at 2:15 pm
Those two separate things, equivalence testing and normality tests. But, yes, you’re correct for both.
Hypotheses are switched for equivalence testing. You need to “work” (i.e., collect a large sample of good quality data) to be able to reject the null that the groups are different to be able to conclude they’re the same.
With typical hypothesis tests, if you have low quality data and a low sample size, you’ll fail to reject the null that they’re the same, concluding they’re equivalent. But that’s more a statement about the low quality and small sample size than anything to do with the groups being equal.
So, equivalence testing make you work to obtain a finding that the groups are the same (at least within some amount you define as a trivial difference).
For normality testing, and other distribution tests, the null states that the data follow the distribution (normal or whatever). If you reject the null, you have sufficient evidence to conclude that your sample data don’t follow the probability distribution. That’s a rare case where you hope to fail to reject the null. And it suffers from the problem I describe above where you might fail to reject the null simply because you have a small sample size. In that case, you’d conclude the data follow the probability distribution but it’s more that you don’t have enough data for the test to register the deviation. In this scenario, if you had a larger sample size, you’d reject the null and conclude it doesn’t follow that distribution.
I don’t know of any equivalence testing type approach for distribution fit tests where you’d need to work to show the data follow a distribution, although I haven’t looked for one either!
February 20, 2022 at 9:26 pm
Is a null hypothesis regularly (always) stated in the negative? “there is no” or “does not”
February 23, 2022 at 9:21 pm
Typically, the null hypothesis includes an equal sign. The null hypothesis states that the population parameter equals a particular value. That value is usually one that represents no effect. In the case of a one-sided hypothesis test, the null still contains an equal sign but it’s “greater than or equal to” or “less than or equal to.” If you wanted to translate the null hypothesis from its native mathematical expression, you could use the expression “there is no effect.” But the mathematical form more specifically states what it’s testing.
It’s the alternative hypothesis that typically contains does not equal.
There are some exceptions. For example, in an equivalence test where the researchers want to show that two things are equal, the null hypothesis states that they’re not equal.
In short, the null hypothesis states the condition that the researchers hope to reject. They need to work hard to set up an experiment and data collection that’ll gather enough evidence to be able to reject the null condition.
February 15, 2022 at 9:32 am
Dear sir I always read your notes on Research methods.. Kindly tell is there any available Book on all these..wonderfull Urgent
Comments and Questions Cancel reply
Article Categories
Book categories, collections.
- Academics & The Arts Articles
- Math Articles
- Statistics Articles
How to Test a Null Hypothesis Based on One Population Proportion
Statistics for dummies.

Sign up for the Dummies Beta Program to try Dummies' newest way to learn.
You can use a hypothesis test to test a statistical claim about a population proportion when the variable is categorical (for example, gender or support/oppose) and only one population or group is being studied (for example, all registered voters).
The test looks at the proportion ( p ) of individuals in the population who have a certain characteristic — for example, the proportion of people who carry cellphones. The null hypothesis is H 0 : p = p 0 , where p 0 is a certain claimed value of the population proportion, p . For example, if the claim is that 70% of people carry cellphones, p 0 is 0.70. The alternative hypothesis is one of the following:
The formula for the test statistic for a single proportion (under certain conditions) is:

and z is a value on the Z -distribution. To calculate the test statistic, do the following:
Calculate the sample proportion,
by taking the number of people in the sample who have the characteristic of interest (for example, the number of people in the sample carrying cellphones) and dividing that by n, the sample size.
where p o is the value in H o .
Calculate the standard error,
Divide your result from Step 2 by your result from Step 3.
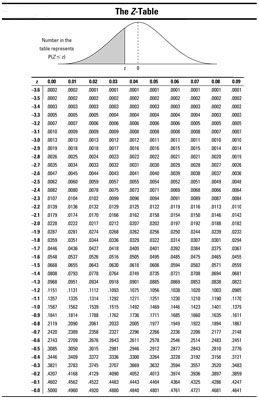
To interpret the test statistic, look up your test statistic on the standard normal ( Z- ) distribution and calculate the p- value.
The conditions for using this test statistic are that
For example, suppose Cavifree claims that four out of five dentists recommend Cavifree toothpaste to their patients. In this case, the population is all dentists, and p is the proportion of all dentists who recommended Cavifree. The claim is that p is equal to “four out of five,” or p 0 is 4 divided by 5 = 0.80. You suspect that the proportion is actually less than 0.80. Your hypotheses are H 0 : p = 0.80 versus H a : p < 0.80.
Suppose that 151 out of your sample of 200 dental patients reported receiving a recommendation for Cavifree from their dentist. To find the test statistic for these results, follow these steps:
and n = 200.
Because p o = 0.80, take p(hat)-p 0 =0.755 – 0.80 = –0.045 as the numerator of the test statistic.
Next, the standard error equals
(the denominator of the test statistic).
The test statistic is
Because the resulting test statistic is negative, it means your sample results are –1.61 standard errors below (less than) the claimed value for the population. How often would you expect to get results like this if H 0 were true? The chance of being at or beyond (in this case less than) –1.61 is 0.0537. (Keep the negative with the number and look up –1.61 in the above Z -table.) This result is your p- value because H a is a less-than hypothesis.
Because the p- value is greater than 0.05 (albeit not by much), you don’t have quite enough evidence for rejecting H 0 . You conclude that the claim that 80% of dentists recommend Cavifree can’t be rejected, according to your data. However, it’s important to report the actual p -value too, so others can make their own decisions.
You might ask, “Hey, the sample proportion of 0.755 is way lower than the claimed proportion of 0.80. Why did the hypothesis test reject H 0 since 0.755 is less than 0.80?” Because in this case, 0.755 is not significantly less than 0.80. You also need to factor in variation using the standard error and the normal distribution to be able to say something about the entire population of dentists.
The letter p is used two different ways in this example: p -value and p . The letter p by itself indicates the population proportion, not the p -value. Don’t get confused. Whenever you report a p -value, be sure you add –value so it’s not confused with p, the population proportion .
About This Article
This article is from the book:.
- Statistics For Dummies ,
About the book author:
Deborah J. Rumsey , PhD, is an Auxiliary Professor and Statistics Education Specialist at The Ohio State University. She is the author of Statistics For Dummies, Statistics II For Dummies, Statistics Workbook For Dummies, and Probability For Dummies.
This article can be found in the category:
- Statistics ,
- Statistics For Dummies Cheat Sheet
- Checking Out Statistical Confidence Interval Critical Values
- Handling Statistical Hypothesis Tests
- Statistically Figuring Sample Size
- Surveying Statistical Confidence Intervals
- View All Articles From Book
Difference in Proportions Hypothesis Test Calculator
Use the calculator below to analyze the results of a difference in two proportions hypothesis test. Enter your sample proportions, sample sizes, hypothesized difference in proportions, test type, and significance level to calculate your results.
You will find a description of how to conduct a difference in proportion hypothesis test below the calculator.
Define the Two Sample z-test
| Significance Level | Difference in Proportions | |
|---|---|---|
| z-score | ||
| Probability |
The Difference Between the Sample Proportions Under the Null Distribution
Conducting a hypothesis test for the difference in proportions.
When two populations rates are related, you can compare them by analyzing the difference between their proportions.
A hypothesis test for the difference in sample proportions can help you make inferences about the relationships between two population proportions.
Note: Difference in proportions hypothesis tests are commonly used in “A/B Tests” in which a researcher compares one rate to another. For example, a digital marketer might use an A/B test to compare a conversion rate from one web advertisement to another version of the same advertisement.
Testing for a Difference in Proportions
For the results of a hypothesis test to be valid, you should follow these steps:
Check Your Conditions
State your hypothesis, determine your analysis plan, analyze your sample, interpret your results.
To use the testing procedure described below, you should check the following conditions:
- Independent Samples – Your samples should be independent of each other.
- Binary Outcomes - When conducting a hypothesis test for the difference in two proportion, each sample point from each sample should consist of only one of two outcomes. We often label one outcome a “success” and the other a “failure,” but it does not matter which of the two outcomes gets which label.
- Success-Failure Rate - Each sample size should be large enough that you see at least 10 “success” and 10 “failures” in each sample. For example, if one of your sample proportions has a 20% or 0.2 “success” rate, then you would need to check that the sample size is at least 50 [20 = 50 * 20%] to meet this condition. This condition helps ensure that the sampling distributions from which you collect your samples reasonably follow the Normal Distribution.
- Simple Random Sampling - You should collect your samples with simple random sampling. This type of sampling requires that every occurrence of a category or event in a population has an equal chance of being selected when taking a sample.
- Sample-to-Population Ratio - For each sample, the population should be much larger than the sample you collect. As a rule-of-thumb, a sample size should represent no more than 5% of its population.
You must state a null hypothesis and an alternative hypothesis to conduct a hypothesis test.
The null hypothesis is a skeptical claim that you would like to test.
The alternative hypothesis represents the alternative claim to the null hypothesis.
Your null hypothesis and alternative hypothesis should be stated in one of three mutually exclusive ways listed in the table below.
| Null Hypothesis | Alternative Hypothesis | Number of Tails | Description |
|---|---|---|---|
| - P = D | - P ≠ D | Tests whether the sample proportions come from populations with a difference in proportions equal to D. If D = 0, then tests if the samples come from populations that are different from each other. | |
| - P ≤ D | - P > D | Tests whether sample one comes from a population with a proportion that is greater than sample two's population proportion by a difference of D. If D = 0, then tests if sample one comes from a population with a proportion greater than sample two's population proportion. | |
| - P ≥ D | - P < D | Tests whether sample one comes from a population with a proportion that is less than sample two's population proportion by a difference of D. If D = 0, then tests if sample one comes from a population with a proportion less than sample two's population proportion. |
D is the hypothesized difference between the populations' proportions that you would like to test.
Before conducting a hypothesis test, you must determine a reasonable significance level, α, or the probability of rejecting the null hypothesis assuming it is true. The lower your significance level, the more confident you can be of the conclusion of your hypothesis test. Common significance levels are 10%, 5%, and 1%.
To evaluate your hypothesis test at the significance level that you set, consider if you are conducting a one or two tail test:
- Two-tail tests divide the rejection region, or critical region, evenly above and below the null distribution, i.e. to the tails of the null sampling distribution. For example, in a two-tail test with a 5% significance level, your rejection region would be the upper and lower 2.5% of the null distribution. An alternative hypothesis of P 1 - P 2 ≠ D requires a two-tail test.
- One-tail tests place the rejection region entirely on one side of the distribution i.e. to the right or left tail of the null distribution. For example, in a one-tail test evaluating if actual population proportion difference D is above the null distribution with a 5% significance level, your rejection region would be the upper 5% of the null distribution. P 1 - P 2 1 - P 2 > D alternative hypotheses require one-tail tests.
The graphical results section of the calculator above shades rejection regions blue.
After checking your conditions, stating your hypothesis, determining your significance level, and collect your sample, you are ready to analyze your hypothesis.
Sample proportions follow the Normal Distribution with the following parameters (i.e. numbers that define the distribution):
- The Difference in the Population Proportions, D - The true difference in the proportions is unknown, but we use the hypothesized difference in the proportions, D, from the null hypothesis in the calculations.
- The Standard Error, SE - The standard error of the difference in the sample proportions can be computed as follows: SE = ((p 1 x (1 – p 1 ))/ n 1 + (p 1 x (1 – p 1 ))/ n 2 ) (1/2) , with n being the sample size. It defines how differences in sample proportions are expected to vary around the null difference in proportions sampling distribution given the sample sizes and under the assumption that the null hypothesis is true.
In a difference in proportions hypothesis test, we calculate the probability that we would observe the difference in sample proportions (p 1 - p 2 ), assuming the null hypothesis is true, also known as the p-value . If the p-value is less than the significance level, then we can reject the null hypothesis.
You can determine a precise p-value using the calculator above, but we can find an estimate of the p-value manually by calculating the z-score as follows: z = (p 1 - p 2 - D) / SE
The z-score is a test statistic that tells us how far our observation is from the difference in proportions given by the null hypothesis under the null distribution. Using any z-score table, we can look up the probability of observing the results under the null distribution. You will need to look up the z-score for the type of test you are conducting, i.e. one or two tail. A hypothesis test for the difference in two proportions is sometimes known as a two proportion z-test because of the use of a z-score in analyzing results.
The conclusion of a hypothesis test for the difference in proportions is always either:
- Reject the null hypothesis
- Do not reject the null hypothesis
If you reject the null hypothesis, you cannot say that your sample difference in proportions is the true difference between the populations. If you do not reject the null hypothesis, you cannot say that the null hypothesis is true.
A hypothesis test is simply a way to look at evidence and conclude if it provides sufficient evidence to reject the null hypothesis.
Example: A/B Test (Hypothesis Test for the Difference in Two Proportions)
Let’s say you are in charge of email marketing for a clothing brand. Your goal is to sell clothes online, and to sell clothes online, you have to get your email recipients to open your emails.
As part of a new email campaign, you have written two versions of an email subject line: an A version and a B version. But you do not know which one will be more effective.
So, you decide to run an “A/B Test” of your subject lines using a difference in proportions hypothesis test to analyze your results. Your goal is to see if either subject line will have a higher "open" rate.
Your email database consists of 100,000 contacts, and you decide to run the test on 5,000 of them with 50% of the sample group receiving subject line A and 50% receiving subject line B. Let’s go through the steps you would take to run the test.
- Check the conditions - Your test consists of binary outcomes (i.e. open and no open), your sample sizes are large enough to meet the success-failure condition but not too large to violate the sample-to-population ratio condition, and you collect your samples using simple random sampling .
- State Your Hypothesis - Your null hypothesis is that the email subject lines are the same (i.e. P 1 - P 2> = 0) and your alternative hypothesis is that they are not the same (i.e. P 1 - P 2> ≠ 0).
- Determine Your Analysis Plan - You believe that a 5% significance level is reasonable. As your test is two-tail test, you will evaluate if the difference in open rates between the samples would occur at the upper or lower 2.5% [2.5% = 5%/2] of the null distribution.
- Analyze Your Sample - After collecting your samples (which you do after steps 1-3), you find that subject line A had a sample open rate, p 1 , of 20%. Subject line B has a sample open rate, p 2 , of 17%. Using the calculator above, you find that a difference in sample proportions of 3% [3% = 20% - 17%] would results in a z-score of 2.73 under the null distribution, which translates to a p-value of 0.63%.
- Interpret Your Results - Since your p-value of 0.63% is less than the significance level of 5%, you have sufficient evidence to reject the null hypothesis.
In this example, you found that you can reject your original claim that the subject lines have the same performance. The test does not guarantee that your subject line A has a higher open rate than subject line B, but it does give you strong reason to favor subject line A.
Statistics Tutorial
Descriptive statistics, inferential statistics, stat reference, statistics - hypothesis testing a proportion.
A population proportion is the share of a population that belongs to a particular category .
Hypothesis tests are used to check a claim about the size of that population proportion.
Hypothesis Testing a Proportion
The following steps are used for a hypothesis test:
- Check the conditions
- Define the claims
- Decide the significance level
- Calculate the test statistic
For example:
- Population : Nobel Prize winners
- Category : Born in the United States of America
And we want to check the claim:
" More than 20% of Nobel Prize winners were born in the US"
By taking a sample of 40 randomly selected Nobel Prize winners we could find that:
10 out of 40 Nobel Prize winners in the sample were born in the US
The sample proportion is then: \(\displaystyle \frac{10}{40} = 0.25\), or 25%.
From this sample data we check the claim with the steps below.
1. Checking the Conditions
The conditions for calculating a confidence interval for a proportion are:
- The sample is randomly selected
- Being in the category
- Not being in the category
- 5 members in the category
- 5 members not in the category
In our example, we randomly selected 10 people that were born in the US.
The rest were not born in the US, so there are 30 in the other category.
The conditions are fulfilled in this case.
Note: It is possible to do a hypothesis test without having 5 of each category. But special adjustments need to be made.
2. Defining the Claims
We need to define a null hypothesis (\(H_{0}\)) and an alternative hypothesis (\(H_{1}\)) based on the claim we are checking.
The claim was:
In this case, the parameter is the proportion of Nobel Prize winners born in the US (\(p\)).
The null and alternative hypothesis are then:
Null hypothesis : 20% of Nobel Prize winners were born in the US.
Alternative hypothesis : More than 20% of Nobel Prize winners were born in the US.
Which can be expressed with symbols as:
\(H_{0}\): \(p = 0.20 \)
\(H_{1}\): \(p > 0.20 \)
This is a ' right tailed' test, because the alternative hypothesis claims that the proportion is more than in the null hypothesis.
If the data supports the alternative hypothesis, we reject the null hypothesis and accept the alternative hypothesis.
Advertisement
3. Deciding the Significance Level
The significance level (\(\alpha\)) is the uncertainty we accept when rejecting the null hypothesis in a hypothesis test.
The significance level is a percentage probability of accidentally making the wrong conclusion.
Typical significance levels are:
- \(\alpha = 0.1\) (10%)
- \(\alpha = 0.05\) (5%)
- \(\alpha = 0.01\) (1%)
A lower significance level means that the evidence in the data needs to be stronger to reject the null hypothesis.
There is no "correct" significance level - it only states the uncertainty of the conclusion.
Note: A 5% significance level means that when we reject a null hypothesis:
We expect to reject a true null hypothesis 5 out of 100 times.
4. Calculating the Test Statistic
The test statistic is used to decide the outcome of the hypothesis test.
The test statistic is a standardized value calculated from the sample.
The formula for the test statistic (TS) of a population proportion is:
\(\displaystyle \frac{\hat{p} - p}{\sqrt{p(1-p)}} \cdot \sqrt{n} \)
\(\hat{p}-p\) is the difference between the sample proportion (\(\hat{p}\)) and the claimed population proportion (\(p\)).
\(n\) is the sample size.
In our example:
The claimed (\(H_{0}\)) population proportion (\(p\)) was \( 0.20 \)
The sample size (\(n\)) was \(40\)
So the test statistic (TS) is then:
\(\displaystyle \frac{0.25-0.20}{\sqrt{0.2(1-0.2)}} \cdot \sqrt{40} = \frac{0.05}{\sqrt{0.2(0.8)}} \cdot \sqrt{40} = \frac{0.05}{\sqrt{0.16}} \cdot \sqrt{40} \approx \frac{0.05}{0.4} \cdot 6.325 = \underline{0.791}\)
You can also calculate the test statistic using programming language functions:
With Python use the scipy and math libraries to calculate the test statistic for a proportion.
With R use the built-in prop.test() function to calculate the test statistic for a proportion.
5. Concluding
There are two main approaches for making the conclusion of a hypothesis test:
- The critical value approach compares the test statistic with the critical value of the significance level.
- The P-value approach compares the P-value of the test statistic and with the significance level.
Note: The two approaches are only different in how they present the conclusion.
The Critical Value Approach
For the critical value approach we need to find the critical value (CV) of the significance level (\(\alpha\)).
For a population proportion test, the critical value (CV) is a Z-value from a standard normal distribution .
This critical Z-value (CV) defines the rejection region for the test.
The rejection region is an area of probability in the tails of the standard normal distribution.
Because the claim is that the population proportion is more than 20%, the rejection region is in the right tail:
Choosing a significance level (\(\alpha\)) of 0.05, or 5%, we can find the critical Z-value from a Z-table , or with a programming language function:
Note: The functions find the Z-value for an area from the left side.
To find the Z-value for a right tail we need to use the function on the area to the left of the tail (1-0.05 = 0.95).
With Python use the Scipy Stats library norm.ppf() function find the Z-value for an \(\alpha\) = 0.05 in the right tail.
With R use the built-in qnorm() function to find the Z-value for an \(\alpha\) = 0.05 in the right tail.
Using either method we can find that the critical Z-value is \(\approx \underline{1.6449}\)
For a right tailed test we need to check if the test statistic (TS) is bigger than the critical value (CV).
If the test statistic is bigger than the critical value, the test statistic is in the rejection region .
When the test statistic is in the rejection region, we reject the null hypothesis (\(H_{0}\)).
Here, the test statistic (TS) was \(\approx \underline{0.791}\) and the critical value was \(\approx \underline{1.6449}\)
Here is an illustration of this test in a graph:
Since the test statistic was smaller than the critical value we do not reject the null hypothesis.
This means that the sample data does not support the alternative hypothesis.
And we can summarize the conclusion stating:
The sample data does not support the claim that "more than 20% of Nobel Prize winners were born in the US" at a 5% significance level .
The P-Value Approach
For the P-value approach we need to find the P-value of the test statistic (TS).
If the P-value is smaller than the significance level (\(\alpha\)), we reject the null hypothesis (\(H_{0}\)).
The test statistic was found to be \( \approx \underline{0.791} \)
For a population proportion test, the test statistic is a Z-Value from a standard normal distribution .
Because this is a right tailed test, we need to find the P-value of a Z-value bigger than 0.791.
We can find the P-value using a Z-table , or with a programming language function:
Note: The functions find the P-value (area) to the left side of Z-value.
To find the P-value for a right tail we need to subtract the left area from the total area: 1 - the output of the function.
With Python use the Scipy Stats library norm.cdf() function find the P-value of a Z-value bigger than 0.791:
With R use the built-in pnorm() function find the P-value of a Z-value bigger than 0.791:
Using either method we can find that the P-value is \(\approx \underline{0.2145}\)
This tells us that the significance level (\(\alpha\)) would need to be bigger than 0.2145, or 21.45%, to reject the null hypothesis.
This P-value is bigger than any of the common significance levels (10%, 5%, 1%).
So the null hypothesis is kept at all of these significance levels.
The sample data does not support the claim that "more than 20% of Nobel Prize winners were born in the US" at a 10%, 5%, or 1% significance level .
Note: It may still be true that the real population proportion is more than 20%.
But there was not strong enough evidence to support it with this sample.
Calculating a P-Value for a Hypothesis Test with Programming
Many programming languages can calculate the P-value to decide outcome of a hypothesis test.
Using software and programming to calculate statistics is more common for bigger sets of data, as calculating manually becomes difficult.
The P-value calculated here will tell us the lowest possible significance level where the null-hypothesis can be rejected.
With Python use the scipy and math libraries to calculate the P-value for a right tailed hypothesis test for a proportion.
Here, the sample size is 40, the occurrences are 10, and the test is for a proportion bigger than 0.20.
With R use the built-in prop.test() function find the P-value for a right tailed hypothesis test for a proportion.
Note: The conf.level in the R code is the reverse of the significance level.
Here, the significance level is 0.05, or 5%, so the conf.level is 1-0.05 = 0.95, or 95%.
Left-Tailed and Two-Tailed Tests
This was an example of a right tailed test, where the alternative hypothesis claimed that parameter is bigger than the null hypothesis claim.
You can check out an equivalent step-by-step guide for other types here:
- Left-Tailed Test
- Two-Tailed Test

COLOR PICKER

Contact Sales
If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]
Report Error
If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]
Top Tutorials
Top references, top examples, get certified.

IMAGES
COMMENTS
What 6 concepts are covered in the Hypothesis Testing for a proportion Calculator? alternative hypothesis. opposite of null hypothesis. One of the proposed proposition in the hypothesis test. H 1. hypothesis testing. statistical test using a statement of a possible explanation for some conclusions. hypothesis testing for a proportion.
Hypothesis Testing Calculator. The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is ...
Calculate the results of a z-test for a proportion. Use the calculator below to analyze the results of a single proportion hypothesis test. Enter your null hypothesis's proportion, sample proportion, sample size, test type, and significance level. You will find a description of how to conduct a hypothesis test of a proportion below the calculator.
hypothesis test for a population Proportion calculator. Fill in the sample size, n, the number of successes, x, the hypothesized population proportion p0 p 0, and indicate if the test is left tailed, <, right tailed, >, or two tailed, ≠ ≠ . Then hit "Calculate" and the test statistic and p-Value will be calculated for you. n: x: p0 p 0
This one proportion z test calculator will allow you to compute the critical values are p-values for this one sample proportion test, that will help you decide whether or not the sample data provides enough evidence to reject the null hypothesis. If instead, what you want to do is to compare two sample proportions, you can use this z-test for ...
This test compares the proportions of two groups to determine if there is a significant difference between them. Here's a step-by-step guide to using the two-proportion z-test for your scenario: ### Hypotheses - **Null Hypothesis (H0)**: There is no difference in the vaccination rates before and after the intervention. \[H_0: p_1 = p_2 \]
Description. The Test for one proportion can be used to test the hypothesis that an observed proportion is equal to a pre-specified proportion.. This test is not performed on data in the data table, but on statistics you enter in a dialog box. Required input. Observed proportion (%): the observed proportion, expressed as a percentage. Sample size: the sample size or total number of observations.
This calculator runs a one sample proportion test for a given sample data set and specified null and alternative hypotheses. In the fields below enter the sample size \(n\) and the number of scores with the trait of interest, \(f\). Enter a value for the null hypothesis. This value should indicate the absence of an effect in your data. It must ...
One sample proportion test (Go to the calculator) We use this test to check if the known proportion is statistically correct, based on the sample proportion and the sample size. the null hypothesis assumes that the known proportion is correct. The statistical decision will be based on the difference between the know proportion and the sample ...
When you calculate the \(p\)-value and draw the picture, the \(p\)-value is the area in the left tail, the right tail, or split evenly between the two tails. ... If the null hypothesis is true (the proportion is 0.25), then there is a 0.0103 probability that the sample (estimated) proportion is 0.4048 \(\left(\frac{17}{42}\right)\) or more ...
Hypothesis test for two sample proportions. sample. Enter a value for the null hypothesis. This value should indicate the absence of an effect in your data. It must be between the values 0 and 1. Indicate whether your alternative hypothesis involves one-tail or two-tails. If it is a one-tailed test, then you need to indicate whether it is a ...
Z Score Calculator for 2 Population Proportions. This is a simple z score calculator that calculates the value of z (and associated p value) for two population proportions. Z Score Calculator. Further Information. ... Null Hypothesis. H0: p1 - p2 = 0, where p1 is the proportion from the first population and p2 the proportion from the second. ...
Instructions: This calculator conducts a Z-test for two population proportions (\(p_1\) and \(p_2\)), Please select the null and alternative hypotheses, type the significance level, the sample sizes, the number of favorable cases (or the sample proportions) and the results of the z-test will be displayed for you:
This test statistic calculator helps to find the static value for hypothesis testing. The calculated test value shows if there's enough evidence to reject a null hypothesis. Also, this calculator performs calculations of either for one population mean, comparing two means, single population proportion, and two population proportions.
Powerful p-value calculator online: calculate statistical significance using a Z-test or T-test statistic (z test calculator / t-test calculator). P-value formula, Z-score formula, T-statistic formula and explanation of the inference procedure. Statistical significance for the difference between two independent groups (unpaired) - proportions (binomial) or means (non-binomial, continuous).
The first step is to state the null hypothesis and an alternative hypothesis. Null hypothesis: P = 0.80. Alternative hypothesis: P ≠ 0.80. Note that these hypotheses constitute a two-tailed test. The null hypothesis will be rejected if the sample proportion is too big or if it is too small. Formulate an analysis plan. For this analysis, the ...
The hypothesis test is based on the Z statistic. The resulting statistic from the test drops into the plot. Red values are tests where the null hypothesis is rejected at the specified level of significance. Change the default significance level (set at 0.05) by adjusting the Level in the applet. 5 tests and 1000 tests add the hypothesis results ...
Fortunately, a one proportion z-test allows us to answer this question. One Proportion Z-Test: Formula. A one proportion z-test always uses the following null hypothesis: H 0: p = p 0 (population proportion is equal to some hypothesized population proportion p 0) The alternative hypothesis can be either two-tailed, left-tailed, or right-tailed:
Hypothesis test for two sample proportions. Enter raw data that is formatted as described on the right: This calculator runs a two sample test of dependent proportions for a given sample data set and specified null and alternative hypotheses. Enter the data in the text area to the left. The data must be formatted with one pair of scores for ...
Null Hypothesis H 0: Group proportions are equal in the population: p 1 = p 2. Alternative Hypothesis H A: Group proportions are not equal in the population: p 1 ≠ p 2. Correlation and Regression Coefficients. Some studies assess the relationship between two continuous variables rather than differences between groups.
The test looks at the proportion (p) of individuals in the population who have a certain characteristic — for example, the proportion of people who carry cellphones.The null hypothesis is H 0: p = p 0, where p 0 is a certain claimed value of the population proportion, p.For example, if the claim is that 70% of people carry cellphones, p 0 is 0.70. The alternative hypothesis is one of the ...
Using the calculator above, you find that a difference in sample proportions of 3% [3% = 20% - 17%] would results in a z-score of 2.73 under the null distribution, which translates to a p-value of 0.63%. Interpret Your Results - Since your p-value of 0.63% is less than the significance level of 5%, you have sufficient evidence to reject the ...
4. Calculating the Test Statistic. The test statistic is used to decide the outcome of the hypothesis test. The test statistic is a standardized value calculated from the sample. The formula for the test statistic (TS) of a population proportion is: p ^ − p p ( 1 − p) ⋅ n.