Hungarian Method

The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.

Hungarian Method to Solve Assignment Problems
The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.
What is an Assignment Problem?
A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.
Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.
Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.
Hungarian Method Steps
Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.
Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.
Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.
Step 3 – Assign zeros
- Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
- Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.
Step 4 – Perform the Optimal Test
- The present assignment is optimal if each row and column has exactly one encircled zero.
- The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.
Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:
(a) Highlight the rows that aren’t assigned.
(b) Label the columns with zeros in marked rows (if they haven’t already been marked).
(c) Highlight the rows that have assignments in indicated columns (if they haven’t previously been marked).
(d) Continue with (b) and (c) until no further marking is needed.
(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.
Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.
Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.
|
|
|---|
Hungarian Method Example
Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.
\(\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
With 5 jobs and 5 men, the stated problem is balanced.
\(\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} \)
Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} \)
When the zeros are assigned, we get the following:
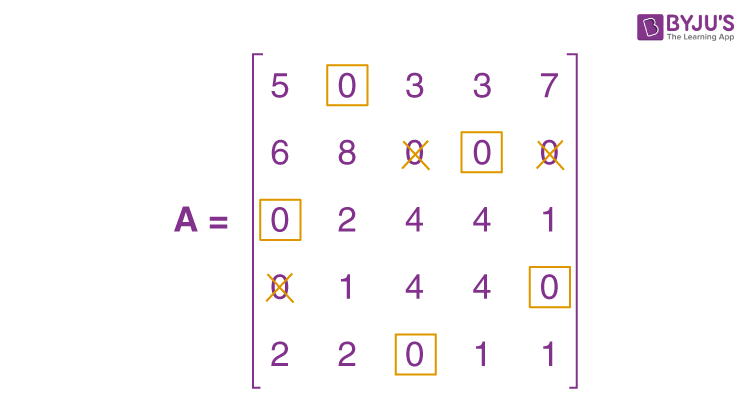
The present assignment is optimal because each row and column contain precisely one encircled zero.
Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.
Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.
Practice Question on Hungarian Method
Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.
\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)
Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.
Frequently Asked Questions on Hungarian Method
What is hungarian method.
The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.
What are the steps involved in Hungarian method?
The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.
What is the purpose of the Hungarian method?
When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
Hungarian algorithm: A step by step guide to assignment method
1. introduction to the hungarian algorithm, 2. understanding the assignment problem, 3. creating the cost matrix, 4. row reduction and column reduction, 5. assigning zeroes and covering lines, 6. finding the minimum number of lines, 7. adjusting the cost matrix, 8. repeating steps 3-7 until optimal assignment is achieved, 9. conclusion and applications of the hungarian algorithm.
The Hungarian Algorithm is a powerful method used to solve the assignment problem, which involves finding the optimal assignment of a set of tasks to a set of resources. This algorithm, also known as the Munkres Algorithm or the Kuhn-Munkres Algorithm, was developed by two mathematicians, Harold Kuhn and James Munkres, in the 1950s. It has since become widely used in various fields such as operations research, computer science, and economics.
From a high-level perspective, the Hungarian Algorithm works by iteratively finding a series of augmenting paths in a weighted bipartite graph. These paths are then used to update the current assignment until an optimal solution is reached. The algorithm guarantees that it will find the best possible assignment with the minimum total cost.
To better understand how the Hungarian Algorithm works, let's delve into its step-by-step process :
1. Constructing the Cost Matrix: The first step is to create a matrix that represents the costs associated with assigning each task to each resource. For example, consider a scenario where four tasks (A, B, C, D) need to be assigned to four resources (W, X, Y, Z). The cost matrix could look like this:
| W | X | Y | Z |
2. Initializing Assignments: Start by initializing an assignment matrix with zeros of the same size as the cost matrix. This matrix will keep track of which tasks are assigned to which resources.
3. Row Reduction: Perform row reduction on the cost matrix by subtracting the smallest element in each row from all other elements in that row. This step ensures that at least one zero is present in each row.
4. Column Reduction: Perform column reduction on the resulting matrix by subtracting the smallest element in each column from all other elements in that column. This step ensures
Introduction to the Hungarian Algorithm - Hungarian algorithm: A step by step guide to assignment method
The assignment problem is a fundamental problem in optimization and operations research . It involves assigning a set of tasks to a set of agents with the objective of minimizing the total cost or maximizing the total profit. Depending on the context, the agents can be workers, machines, or any other entities capable of performing the tasks. Similarly, the tasks can be jobs, projects, or any other activities that require the attention of the agents. The assignment problem arises in various applications, such as scheduling, logistics, resource allocation, and matching.
To solve the assignment problem, we need a method that can determine an optimal or near-optimal assignment. The Hungarian algorithm is a well-known method that can solve the assignment problem efficiently. It is based on the principle of duality and the concept of augmenting paths. The algorithm can handle both balanced and unbalanced assignment problems, and it can find a unique solution in polynomial time.
Here are some key insights about the assignment problem:
1. The assignment problem can be formulated as a linear programming problem, where the objective function and the constraints are linear. The linear programming formulation can be solved using various algorithms, such as the simplex method, the interior-point method, or the network simplex method. However, the Hungarian algorithm is preferred for its simplicity and efficiency.
2. The assignment problem can be represented as a bipartite graph, where the agents and the tasks are the two partitions of the graph. The edges of the graph are the costs or profits associated with each assignment. The Hungarian algorithm works by finding a maximum matching in the graph, which corresponds to an optimal assignment.
3. The Hungarian algorithm can be implemented using different variants, such as the matrix-based variant, the path-based variant, or the Hungarian-Ford-Fulkerson variant. Each variant has its advantages and disadvantages, depending on the size and sparsity of the input matrix.
4. The Hungarian algorithm can be extended to handle additional constraints, such as capacity constraints, precedence constraints, or multi-objective criteria. For example, if the agents have different capacities or skills, we can add capacity constraints to ensure that each agent is assigned to at most one task. If the tasks have different priorities or deadlines, we can add precedence constraints to ensure that some tasks are assigned before others. If the objective is to minimize both the cost and the time, we can use a multi-objective approach that balances the two criteria.
The assignment problem is a crucial problem in optimization and operations research, and the Hungarian algorithm is a powerful method that can solve it efficiently. By understanding the principles and insights of the assignment problem, we can apply the Hungarian algorithm to various applications and achieve optimal or near-optimal solutions.
Understanding the Assignment Problem - Hungarian algorithm: A step by step guide to assignment method
In the Hungarian algorithm, the first step is to create a cost matrix. This matrix represents the costs of assigning each worker to each task. The cost of assigning a worker to a task can be anything, but in most practical applications, the cost represents the efficiency or quality of the assignment. For example, if you are trying to assign workers to build a house, the cost of assigning a worker to a task might represent their skill level or experience in that particular task.
Creating the cost matrix is a crucial step in the Hungarian algorithm, as it forms the basis for the rest of the algorithm. There are a few different ways to create the cost matrix, depending on the specific problem you are trying to solve. Here are some methods that can be used to create the cost matrix:
1. Manual input: If you have a small number of workers and tasks, you can simply input the cost of assigning each worker to each task manually. For example, if you have 3 workers and 3 tasks, you could create a 3x3 matrix by inputting the costs like this:
| Task 1 | Task 2 | Task 3 |
2. Distance matrix: If you are trying to assign tasks to workers based on their proximity to the task location, you can create a distance matrix. This matrix represents the distance between each worker and task location. The cost of assigning a worker to a task can then be calculated based on the distance between the two points.
3. Machine learning: In some cases, it may be possible to use machine learning algorithms to create the cost matrix. For example, if you are trying to assign workers to sales leads, you could use a machine learning algorithm to predict the likelihood of each worker closing a particular sale. The cost of assigning a worker to a task could then be based on this prediction.
Overall, creating the cost matrix is a critical step in the Hungarian algorithm. By carefully considering the costs of assigning each worker to each task, you can use the algorithm to find the optimal assignment that minimizes the total cost.
Creating the Cost Matrix - Hungarian algorithm: A step by step guide to assignment method
Once the cost matrix has been modified to have equal number of rows and columns, the next step is to reduce the matrix by row and column operations . This step is crucial in order to determine which cells will be assigned to each other, ultimately resulting in the final assignment.
From the perspective of linear algebra, row reduction and column reduction can be viewed as transforming the matrix into its reduced row echelon form (RREF), which is the matrix's most simplified form. This is done by performing elementary row operations, such as swapping two rows, multiplying a row with a constant, or adding a multiple of one row to another. The same operations are performed for columns, resulting in the reduced column echelon form.
Here are the steps involved in row reduction and column reduction:
1. Identify the smallest number in each row and subtract it from every element in that row. This ensures that there is at least one zero in each row.
2. Do the same for each column by finding the smallest number in each column and subtracting it from every element in that column. This ensures that there is at least one zero in each column.
3. Draw lines through the rows and columns that contain zeros. The goal is to draw the minimum number of lines required to cover all the zeros.
4. If the number of lines drawn is equal to the number of rows or columns, the matrix is fully optimized and the assignment can be made. If not, proceed to step 5.
5. Find the smallest uncovered number in the matrix and subtract it from all uncovered numbers. Then, add it to all numbers that are covered by two lines. This step is known as the "assignment step".
6. Repeat steps 3-5 until the matrix is fully optimized and the assignment can be made.
For example, consider the following cost matrix:
| | Job 1 | Job 2 | Job 3 |
| W | 8 | 6 | 5 |
| X | 5 | 4 | 7 |
| Y | 8 | 4 | 6 |
After subtracting the smallest number in each row and column, the matrix becomes:
| W | 3 | 1 | 0 |
| X | 1 | 0 | 3 |
| Y | 4 | 0 | 2 |
The minimum number of lines required to cover all the zeros is 2 (one horizontal and one vertical line). This means that two assignments can be made. The assignment step involves subtracting the smallest uncovered number (which is 1) from all uncovered numbers, and adding it to all numbers that are covered by two lines. After this step, the matrix becomes:
| W | 2 | 0 | 0 |
| X | 0 | 0 | 2 |
| Y | 3 | 0 | 1 |
The minimum number of lines required to cover all the zeros is still 2. The next assignment can be made between (W, Job 2) and (X, Job 1). After subtracting the smallest uncovered number (which is 2) from all uncovered numbers, and adding it to all numbers that are covered by two lines, the matrix becomes:
| W | 0 | 0 | 0 |
| X | 0 | 0 | 0 |
| Y | 1 | 0 | 0 |
The minimum number of lines required to cover all the zeros is now 3, which is equal to the number of rows. This means that the matrix is fully optimized and the final assignment is (W, Job 2), (X, Job 1), and (Y, Job 3).
Row Reduction and Column Reduction - Hungarian algorithm: A step by step guide to assignment method
After completing the second step of the Hungarian algorithm, which involves finding the minimum number of lines required to cover all the zeros in the cost matrix, we move on to step three: assigning zeroes and covering lines. This step is crucial in determining the optimal assignment of tasks or resources in various real-world scenarios such as job scheduling, transportation planning, or project management.
Assigning zeroes and covering lines is a process that aims to identify an assignment that maximizes efficiency and minimizes costs. It involves making strategic choices based on the positions of zeroes in the cost matrix and the lines that have been drawn to cover them. This step requires careful analysis from different perspectives to ensure an optimal solution.
From a mathematical standpoint, assigning zeroes and covering lines can be seen as a game of strategy. The goal is to find a combination of assignments that yields the lowest possible total cost. Each zero represents a potential assignment, and by covering lines, we limit the number of assignments available for each row and column.
To better understand this step, let's delve into some key insights:
1. Assigning Zeroes:
- Start by selecting a row or column with only one uncovered zero.
- Assign this zero to its corresponding task or resource.
- Cross out all other zeroes in the same row or column.
For example, consider a 3x3 cost matrix where we have identified a row with only one uncovered zero:
We assign the zero in row 1, column 2 (highlighted) to its corresponding task. The updated matrix becomes:
| 2 | X | 1 |
| X | 3 | 2 |
2. Covering Lines:
- If all rows and columns are covered, the assignment is complete.
- If not, draw lines through all rows that do not contain assignments and all columns that have been covered.
- The minimum number of lines required to cover all zeros determines the next step.
Continuing from the previous example, let's assume we have covered row 1 and column 2. The updated matrix becomes:
| X | X | 1 |
Assigning Zeroes and Covering Lines - Hungarian algorithm: A step by step guide to assignment method
Once we have completed the step of subtracting the minimum value from each row and column, it is time to move on to finding the minimum number of lines required to cover all the zeros in the matrix. This step is crucial in determining the optimal assignment of tasks or resources using the Hungarian algorithm.
From a high-level perspective, finding the minimum number of lines involves drawing lines through rows and columns in such a way that all zeros are covered. These lines will help us identify potential assignments and determine if any additional steps are needed to achieve an optimal solution .
Looking at this step from different points of view can provide valuable insights into its significance:
1. Mathematical Perspective:
- The minimum number of lines represents the maximum number of independent zeros that can be assigned without conflicts.
- By covering all zeros with a minimum number of lines, we ensure that each task or resource is assigned exactly once.
2. Graph Theory Perspective:
- The matrix can be represented as a bipartite graph, where rows and columns are nodes, and zeros represent edges between them.
- Drawing lines through rows and columns is equivalent to finding a matching in this bipartite graph.
- The minimum number of lines corresponds to finding a maximum matching, ensuring that no two edges share a common node.
To better understand this step, let's break it down into a numbered list:
1. Start by identifying rows or columns that contain only one zero. These single zeros must be assigned immediately, so draw a line through their respective row or column.
Example: Consider a 3x3 matrix with the following zeros: (1,2), (2,1), and (3,3). In this case, we would draw lines through rows 1 and 2 since they contain single zeros.
2. If there are still uncovered zeros remaining in either rows or columns, proceed to identify rows or columns with the fewest uncovered zeros. Draw lines through these rows or columns.
Example: Continuing from the previous example, if there are additional zeros at (1,1) and (3,2), we would draw a line through column 2 since it has the fewest uncovered zeros.
3. Repeat step 2 until all zeros are covered. This may involve drawing multiple lines through rows or columns.
Example: If there is an additional zero at (2,3), we would draw a line through row 2 to cover it.
Finding the Minimum Number of Lines - Hungarian algorithm: A step by step guide to assignment method
After completing the fourth step of the Hungarian algorithm, which involves finding the minimum number of lines to cover all zeros in the cost matrix, we move on to the fifth step: adjusting the cost matrix. This step is crucial as it allows us to further refine our assignment and improve its optimality. By making adjustments to the cost matrix, we can potentially reduce the overall cost of the assignment and achieve a more efficient solution.
From different perspectives, adjusting the cost matrix can be seen as a way to fine-tune the initial assignments made in step three or as a means to explore alternative assignments that may yield better results. Regardless of how one perceives it, this step plays a significant role in optimizing the assignment method.
To provide a comprehensive understanding of this step, let's delve into some key aspects through a numbered list:
1. Subtracting the Smallest Uncovered Value: In this adjustment technique, we identify the smallest value that is not covered by any line (neither horizontal nor vertical) and subtract it from all uncovered values. This adjustment reduces the overall cost of the assignment without altering any existing assignments.
For example, consider a 3x3 cost matrix where we have already assigned values to some cells:
The smallest uncovered value is 6. By subtracting 6 from all uncovered values, we obtain:
This adjustment ensures that no uncovered value remains positive, making it easier to find an optimal solution.
2. Adding Values at Intersection Points: Another adjustment technique involves adding values at intersection points where two lines intersect (one horizontal and one vertical). These intersection points represent potential assignments that were not initially considered due to constraints imposed by the lines.
For instance, consider a 4x4 cost matrix with assigned values:
In this case, there are two intersection points: (1,3) and (3,1). By adding the values at these points (0 + 0 = 0), we can include them as potential assignments:
Adjusting the Cost Matrix - Hungarian algorithm: A step by step guide to assignment method
In the Hungarian algorithm, achieving an optimal assignment involves repeating steps 3-7 until the best possible solution is obtained. This iterative process allows for refining the initial assignment and finding the most efficient allocation of resources . By continuously adjusting the assignments based on cost and availability, the algorithm aims to minimize the overall cost or maximize the overall benefit of the assignment.
From a practical standpoint, repeating steps 3-7 ensures that all possibilities are explored and evaluated before settling on a final assignment. It allows for flexibility in decision-making , as adjustments can be made at each iteration to improve the overall outcome. This iterative approach is particularly useful when dealing with complex problems that require multiple iterations to reach an optimal solution.
To better understand this process, let's break it down into a numbered list:
1. Start with an initial assignment: Begin by assigning values to each element in the cost matrix based on their respective costs or benefits. This initial assignment serves as a starting point for further iterations.
2. Find a feasible solution: Apply steps 3-7 of the Hungarian algorithm to find a feasible solution. This involves identifying rows and columns with zeros and assigning them accordingly to create a complete set of assignments.
3. Evaluate the current assignment: calculate the total cost or benefit of the current assignment based on the assigned elements in the cost matrix. This provides a measure of how well the current solution performs.
4. Check for optimality: Determine if the current assignment is optimal by examining whether all rows and columns have been assigned exactly once. If so, proceed to step 6; otherwise, continue to step 5.
5. Modify the assignment: Identify any unassigned rows or columns and adjust the assignments to improve the overall solution. This may involve modifying existing assignments or adding new ones based on available options.
6. Repeat steps 3-7: Return to step 3 and repeat the process using the modified assignment from step 5. This iterative loop allows for continuous refinement of the assignment until an optimal solution is achieved.
7. Track the best solution: Keep track of the best assignment found so far, as subsequent iterations may yield better results. This ensures that the algorithm does not settle for a suboptimal solution prematurely.
By repeating steps 3-7, the Hungarian algorithm gradually converges towards an optimal assignment by iteratively adjusting and evaluating the assignments. This iterative nature allows for flexibility in decision-making and enables the algorithm to explore different possibilities before settling on the best allocation of resources.
Repeating Steps 3 7 until Optimal Assignment is Achieved - Hungarian algorithm: A step by step guide to assignment method
The Hungarian Algorithm is a powerful tool that has proven to be highly effective in solving assignment problems . In this section, we will explore the conclusion and applications of this algorithm, shedding light on its significance from various perspectives.
1. Efficiency: One of the key advantages of the Hungarian Algorithm is its efficiency in finding an optimal solution to assignment problems. The algorithm has a time complexity of O(n^3), where n represents the number of rows or columns in the cost matrix. This makes it suitable for solving large-scale assignment problems efficiently .
For example, let's consider a scenario where a company needs to assign tasks to its employees based on their skills and preferences. Using the Hungarian Algorithm, the company can quickly determine the best possible assignments, minimizing costs and maximizing productivity.
2. Optimality: The Hungarian Algorithm guarantees an optimal solution to assignment problems. It ensures that the total cost or objective function value is minimized or maximized, depending on the problem at hand. This optimality property makes it a reliable choice for decision-making processes.
Suppose a hospital needs to assign doctors to different shifts while considering their availability and expertise. By applying the Hungarian Algorithm, the hospital can ensure that each shift is staffed with the most suitable doctors, optimizing patient care and resource allocation.
3. Versatility: The Hungarian Algorithm is not limited to traditional assignment problems alone; it can also be adapted for other optimization tasks. For instance, it can be used for solving transportation problems, job scheduling, facility location, and more.
Let's take an example of a logistics company that needs to determine the most efficient routes for delivering goods to various destinations. By formulating this problem as an assignment problem and applying the Hungarian Algorithm, the company can identify the optimal route assignments, minimizing fuel consumption and delivery time.
4. real-world applications : The Hungarian Algorithm finds applications in diverse fields such as operations research, computer science, economics, and engineering. Its ability to solve complex optimization problems efficiently has made it a valuable tool in various industries.
For instance, in the field of computer vision, the Hungarian Algorithm is used for object tracking and matching. It helps in associating objects across multiple frames of a video, enabling applications like surveillance, motion analysis, and augmented reality.
The Hungarian Algorithm offers an efficient and optimal solution to assignment problems, making it a valuable tool in decision-making processes. Its versatility and real-world applications further highlight its significance in various domains. By understanding and applying this algorithm, individuals and organizations can tackle complex optimization
Conclusion and Applications of the Hungarian Algorithm - Hungarian algorithm: A step by step guide to assignment method
Read Other Blogs
Interactive media has revolutionized the way users engage with content, offering a dynamic platform...
When it comes to funding a project, there are a variety of options available to businesses. One...
Loan financing for startups can be a great way to get your business off the ground. The application...
CRO research is the process of understanding your website visitors, their behavior, preferences,...
Leverage is a double-edged sword in the financial markets, capable of amplifying both gains and...
Value Stream Mapping (VSM) is a pivotal tool in the lean manufacturing methodology, a technique...
When it comes to launching a startup, one of the most important steps is getting press and...
Understanding the basics of a federal tax lien is crucial for anyone dealing with tax issues or...
In the realm of entrepreneurial culture development, the genesis of innovation is not merely an...
- DOI: 10.1007/978-3-540-68279-0_2
- Corpus ID: 9426884
The Hungarian method for the assignment problem
- Published in 50 Years of Integer… 1 March 1955
Mathematics
- Naval Research Logistics (NRL)
11,772 Citations
A note on hungarian method for solving assignment problem, the optimal assignment problem: an investigation into current solutions, new approaches and the doubly stochastic polytope, an effective algorithm to solve assignment problems : opportunity cost approach, optimal assignment problem on record linkage, an application of the hungarian algorithm to solve traveling salesman problem.
- Highly Influenced
Heuristic algorithms and learning techniques: applications to the graph coloring problem
A simulation of the faculty-assignment problem: an integer programming approach, computational studies of randomized multidimensional assignment problems, optimal solution of an assignment problem as a special case of transportation problem, assignment problems by, 17 references, a combinatorial algorithm, solution of the personnel classification problem with the method of optimal regions, the problem of classification of personnel, history of mathematical programming : a collection of personal reminiscences, on representatives of subsets, on a personnel assignment problem, on the hitchcock distribution problem, 1. a certain zero-sum two-person game equivalent to the optimal assignment problem, über graphen und ihre anwendung auf determinantentheorie und mengenlehre, related papers.
Showing 1 through 3 of 0 Related Papers
- Practice Mathematical Algorithm
- Mathematical Algorithms
- Pythagorean Triplet
- Fibonacci Number
- Euclidean Algorithm
- LCM of Array
- GCD of Array
- Binomial Coefficient
- Catalan Numbers
- Sieve of Eratosthenes
- Euler Totient Function
- Modular Exponentiation
- Modular Multiplicative Inverse
- Stein's Algorithm
- Juggler Sequence
- Chinese Remainder Theorem
- Quiz on Fibonacci Numbers
Hungarian Algorithm for Assignment Problem | Set 2 (Implementation)
Given a 2D array , arr of size N*N where arr[i][j] denotes the cost to complete the j th job by the i th worker. Any worker can be assigned to perform any job. The task is to assign the jobs such that exactly one worker can perform exactly one job in such a way that the total cost of the assignment is minimized.
Input: arr[][] = {{3, 5}, {10, 1}} Output: 4 Explanation: The optimal assignment is to assign job 1 to the 1st worker, job 2 to the 2nd worker. Hence, the optimal cost is 3 + 1 = 4. Input: arr[][] = {{2500, 4000, 3500}, {4000, 6000, 3500}, {2000, 4000, 2500}} Output: 4 Explanation: The optimal assignment is to assign job 2 to the 1st worker, job 3 to the 2nd worker and job 1 to the 3rd worker. Hence, the optimal cost is 4000 + 3500 + 2000 = 9500.
Different approaches to solve this problem are discussed in this article .
Approach: The idea is to use the Hungarian Algorithm to solve this problem. The algorithm is as follows:
- For each row of the matrix, find the smallest element and subtract it from every element in its row.
- Repeat the step 1 for all columns.
- Cover all zeros in the matrix using the minimum number of horizontal and vertical lines.
- Test for Optimality : If the minimum number of covering lines is N , an optimal assignment is possible. Else if lines are lesser than N , an optimal assignment is not found and must proceed to step 5.
- Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.
Consider an example to understand the approach:
Let the 2D array be: 2500 4000 3500 4000 6000 3500 2000 4000 2500 Step 1: Subtract minimum of every row. 2500, 3500 and 2000 are subtracted from rows 1, 2 and 3 respectively. 0 1500 1000 500 2500 0 0 2000 500 Step 2: Subtract minimum of every column. 0, 1500 and 0 are subtracted from columns 1, 2 and 3 respectively. 0 0 1000 500 1000 0 0 500 500 Step 3: Cover all zeroes with minimum number of horizontal and vertical lines. Step 4: Since we need 3 lines to cover all zeroes, the optimal assignment is found. 2500 4000 3500 4000 6000 3500 2000 4000 2500 So the optimal cost is 4000 + 3500 + 2000 = 9500
For implementing the above algorithm, the idea is to use the max_cost_assignment() function defined in the dlib library . This function is an implementation of the Hungarian algorithm (also known as the Kuhn-Munkres algorithm) which runs in O(N 3 ) time. It solves the optimal assignment problem.
Below is the implementation of the above approach:
Time Complexity: O(N 3 ) Auxiliary Space: O(N 2 )
Please Login to comment...
Similar reads.
- Mathematical
- OpenAI o1 AI Model Launched: Explore o1-Preview, o1-Mini, Pricing & Comparison
- How to Merge Cells in Google Sheets: Step by Step Guide
- How to Lock Cells in Google Sheets : Step by Step Guide
- PS5 Pro Launched: Controller, Price, Specs & Features, How to Pre-Order, and More
- #geekstreak2024 – 21 Days POTD Challenge Powered By Deutsche Bank
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
Hungarian Algorithm Introduction & Python Implementation
How to use hungarian method to resolve the linear assignment problem..
By Eason on 2021-08-02
In this article, I will introduce how to use Hungarian Method to resolve the linear assignment problem and provide my personal Python code solution.
So… What is the linear assignment problem?
The linear assignment problem represents the need to maximize the available resources (or minimize the expenditure) with limited resources. For instance, below is a 2D matrix, where each row represents a different supplier, and each column represents the cost of employing them to produce a particular product. Each supplier can only specialize in the production of one of these products. In other words, only one element can be selected for each column and row in the matrix, and the sum of the selected elements must be minimized (minimized cost expense).
The cost of producing different goods by different producers:
Indeed, this is a simple example. By trying out the possible combinations, we can see that the smallest sum is 13, so supplier A supplies Bubble Tea , supplier B supplies milk tea, and supplier C supplies Fruit Tea . However, such attempts do not follow a clear rule and become inefficient when applied to large tasks. Therefore, the next section will introduce step by step the Hungarian algorithm, which can be applied to the linear assignment problem.
Hungarian Algorithm & Python Code Step by Step
In this section, we will show how to use the Hungarian algorithm to solve linear assignment problems and find the minimum combinations in the matrix. Of course, the Hungarian algorithm can also be used to find the maximum combination.
Step 0. Prepare Operations
First, an N by N matrix is generated to be used for the Hungarian algorithm (Here, we use a 5 by 5 square matrix as an example).
The above code randomly generates a 5x5 cost matrix of integers between 0 and 10.
If we want to find the maximum sum, we could do the opposite. The matrix to be solved is regarded as the profit matrix, and the maximum value in the matrix is set as the common price of all goods. The cost matrix is obtained by subtracting the profit matrix from the maximum value. Finally, the cost matrix is substituted into the Hungarian algorithm to obtain the minimized combination and then remapped back to the profit matrix to obtain the maximized sum value and composition result.
The above code randomly generates a 5x5 profit matrix of integers between 0 and 10 and generate a corresponding cost matrix
By following the steps above, you can randomly generate either the cost matrix or the profit matrix. Next, we will move into the introduction of the Hungarian algorithm, and for the sake of illustration, the following sections will be illustrated using the cost matrix shown below. We will use the Hungarian algorithm to solve the linear assignment problem of the cost matrix and find the corresponding minimum sum.
Example cost matrix:
Step 1. Every column and every row subtract its internal minimum
First, every column and every row must subtract its internal minimum. After subtracting the minimum, the cost matrix will look like this.
Cost matrix after step 1:
And the current code is like this:
Step 2.1. Min_zero_row Function Implementation
At first, we need to find the row with the fewest zero elements. So, we can convert the previous matrix to the boolean matrix(0 → True, Others → False).
Transform matrix to boolean matrix:
Corresponding Boolean matrix:
Therefore, we can use the “min_zero_row” function to find the corresponding row.
The row which contains the least 0:

Third, mark any 0 elements on the corresponding row and clean up its row and column (converts elements on the Boolean matrix to False). The coordinates of the element are stored in mark_zero.
Hence, the boolean matrix will look like this:
The boolean matrix after the first process. The fourth row has been changed to all False.
The process is repeated several times until the elements in the boolean matrix are all False. The below picture shows the order in which they are marked.
The possible answer composition:

Step 2.2. Mark_matrix Function Implementation
After getting Zero_mat from the step 2–1, we can check it and mark the matrix according to certain rules. The whole rule can be broken down into several steps:
- Mark rows that do not contain marked 0 elements and store row indexes in the non_marked_row
- Search non_marked_row element, and find out if there are any unmarked 0 elements in the corresponding column
- Store the column indexes in the marked_cols
- Compare the column indexes stored in marked_zero and marked_cols
- If a matching column index exists, the corresponding row_index is saved to non_marked_rows
- Next, the row indexes that are not in non_marked_row are stored in marked_rows
Finally, the whole mark_matrx function is finished and then returns marked_zero , marked_rows , marked_cols. At this point, we will be able to decide the result based on the return information.
If we use the example cost matrix, the corresponding marked_zero , marked_rows, and marked_cols are as follows:
- marked_zero : [(3, 2), (0, 4), (1, 1), (2, 0), (4, 3)]
- marked_rows : [0, 1, 2, 3, 4]
- marked_cols : []
Step 3. Identify the Result
At this step, if the sum of the lengths of marked_rows and marked_cols is equal to the length of the cost matrix, it means that the solution of the linear assignment problem has been found successfully, and marked_zero stores the solution coordinates. Fortunately, in the example matrix, we find the answer on the first try. Therefore, we can skip to step 5 and calculate the solution.
However, everything is hardly plain sailing. Most of the time, we will not find the solution on the first try, such as the following matrix:
After Step 1 & 2 , the corresponding matrix, marked_rows, and marked_cols are as follows:
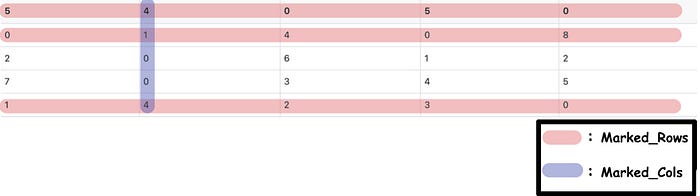
The sum of the lengths of Marked_Rows and Marked_Cols is 4 (less than 5).
Apparently, the sum of the lengths is less than the length of the matrix. At this time, we need to go into Step 4 to adjust the matrix.
Step 4. Adjust Matrix
In Step 4, we're going to put the matrix after Step 1 into the Adjust_Matrix function . Taking the latter matrix in Step 3 as an example, the matrix to be modified in Adjust_Matrix is:
The whole function can be separated into three steps:
- Find the minimum value for an element that is not in marked_rows and not in marked_cols . Hence, we can find the minimum value is 1.
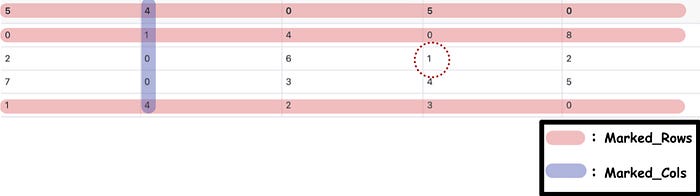
- Subtract the elements which not in marked_rows nor marked_cols from the minimum values obtained in the previous step.
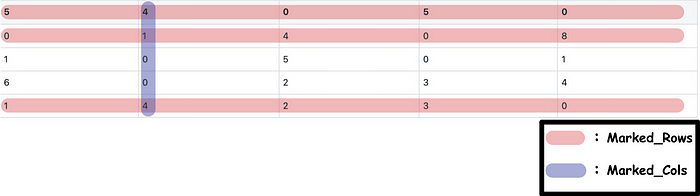
- Add the element in marked_rows , which is also in marked_cols , to the minimum value obtained by Step 4–1.

Return the adjusted matrix and repeat Step 2 and Step 3 until the conditions satisfy the requirement of entering Step 5.
Step 5. Calculate the Answer
Using the element composition stored in marked_zero , the minimum and maximum values of the linear assignment problem can be calculated.

The minimum composition of the assigned matrix and the minimum sum is 18.

The maximum composition of the assigned matrix and the maximum sum is 43.
The code of the Answer_Calculator function is as follows:
The complete code is as follows:
Hungarian algorithm - Wikipedia

Continue Learning
How to make your loop way faster in python.
Python slow? Heres how to make your loops way faster
Create Your Own PDF Question Answering System with OpenAI GPT, LangChain, and Streamlit
How to create a chatbot using OpenAI’s GPT language model and the Streamlit library for Python.
Turn your Python Script into a 'Real' Program with Docker
No one cares if you can reverse a linked list — they want a one-click way to use your software on their machine. Docker makes that possible.
Five Unbelievable Open-Source Object Detection Projects Ready to Use in 2022
Interactive visualizations with pandas, seaborn and ipywidgets.
Create dynamic charts, save a ton of time.
10 Python Automation Scripts for Everyday Problems
Collection of Handy Tools for your Daily Python Projects
Improvement in Hungarian Algorithm for Assignment Problem
- Conference paper
- First Online: 01 January 2014
- Cite this conference paper

- Kartik Shah 5 ,
- Praveenkumar Reddy 5 &
- S. Vairamuthu 5
Part of the book series: Advances in Intelligent Systems and Computing ((AISC,volume 324))
2517 Accesses
6 Citations
Hungarian method for assignment problem is generally used in parallel environment for the assignment of job to a processor. If the number of processors and number of jobs are same, then we can assign each processor 1 job with less cost using Hungarian method. If the number of jobs is larger compared to number of processors, then this method does not work (another approach is using dummy processors, but it is not implementable). In this paper, we proposed an alternate approach same as Hungarian method for assignment of more jobs to lesser processors.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Available as EPUB and PDF
- Compact, lightweight edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
Similar content being viewed by others

A note of reduced dimension optimization algorithm of assignment problem

Load Balancing of Unbalanced Matrix with Hungarian Method

Heuristics-based on the Hungarian Method for the Patient Admission Scheduling Problem
W. Kuhn, The hungarian method for assignment problem. Nav. Res. Logistics Q. 2 , 83–87 (1955)
Article Google Scholar
D.P. Bertsekas, Linear network optimization algorithms and codes (MIT Press, Cambridge, 1991)
MATH Google Scholar
G. Carpaneto, S. Martello, P. Toth, Algorithms and codes for assignment problem. Ann. Oper. Res. 13 , 193–223 (1988)
Article MathSciNet Google Scholar
D.A. Castanon, B. Smith, A. Wilson, Performance of parallel assignment algorithms on different multiprocessor architectures . Alphatech report TP-1245, Burlington, MA, (1989)
Google Scholar
U. Derigs, The shortest augmenting path method for solving assignment problem-motivation and computational experience. Ann. Oper. Res. 4 , 57–102 (1985)
M. Engqust, A successive shortest path algorithm for the assignment problem. INFRO. 20 , 370–384 (1982)
F. Glover, R. Glover, D. Klingman, Threshold assignment algorithm. Centre for Business Decision analysis report CBDA 107, Graduate School of Business, University of Taxes at Austin (1982)
J.R.M. Hall, An algorithm for distinct representatives. Am. Math. Monthly 51 , 716–717 (1956)
R. Jonkar, A. Volgenant, A shortest augmenting path algorithm for the dense and sparse linear assignment problems. Computing 3 , 92–106 (1987)
E. Lawler, Combinational Optimization: Networks and Matroids (Holt, Rinehart & Winston, New York, 1976), p. 206
L.F. Mcginnis, Implementation and testing of a primal dual algorithm for the assignment problem. Oper. Res. Int. J. 31 , 277–291 (1983)
MATH MathSciNet Google Scholar
C.H. Papadimitriou, K. Steiglitz, Combinational Optimization: Algorithm and complexity (Prentice-Hall, Englewood Cliffs, 1982)
E. Balas, D. Miller, J. Pekny, P. Toth, A parallel shortest path algorithm for assignment problem. J. ACM 38 (4), 985–1004 (1991)
Article MATH MathSciNet Google Scholar
Download references
Acknowledgments
The authors would like to thank the School of Computer Science and Engineering, VIT University, for giving them the opportunity to carry out this project and also for providing them with the requisite resources and infrastructure for carrying out the research.
Author information
Authors and affiliations.
School of Computing Science and Engineering, VIT University, Vellore, 632014, India
Kartik Shah, Praveenkumar Reddy & S. Vairamuthu
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Kartik Shah .
Editor information
Editors and affiliations.
Electrical & Electronics Engineering, Noorul Islam Centre for Higher Education, Kumaracoil, Tamil Nadu, India
L. Padma Suresh
Electrical and Electronics Engineering, SRM Engineering College, Kattankulathur, Tamil Nadu, India
Subhransu Sekhar Dash
Electrical Engineering, IIT Delhi, New Delhi, Delhi, India
Bijaya Ketan Panigrahi
Rights and permissions
Reprints and permissions
Copyright information
© 2015 Springer India
About this paper
Cite this paper.
Shah, K., Reddy, P., Vairamuthu, S. (2015). Improvement in Hungarian Algorithm for Assignment Problem. In: Suresh, L., Dash, S., Panigrahi, B. (eds) Artificial Intelligence and Evolutionary Algorithms in Engineering Systems. Advances in Intelligent Systems and Computing, vol 324. Springer, New Delhi. https://doi.org/10.1007/978-81-322-2126-5_1
Download citation
DOI : https://doi.org/10.1007/978-81-322-2126-5_1
Published : 02 November 2014
Publisher Name : Springer, New Delhi
Print ISBN : 978-81-322-2125-8
Online ISBN : 978-81-322-2126-5
eBook Packages : Engineering Engineering (R0)
Share this paper
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research
Index Assignment problem Hungarian algorithm Solve online
The assignment problem
The assignment problem deals with assigning machines to tasks, workers to jobs, soccer players to positions, and so on. The goal is to determine the optimum assignment that, for example, minimizes the total cost or maximizes the team effectiveness.
Read more on the assignment problem
The Hungarian algorithm
The Hungarian algorithm is an easy to understand and easy to use algorithm that solves the assignment problem.
A step by step explanation of the algorithm
Solve your own problem online
HungarianAlgorithm.com © 2013-2024
Information
- Author Services
Initiatives
You are accessing a machine-readable page. In order to be human-readable, please install an RSS reader.
All articles published by MDPI are made immediately available worldwide under an open access license. No special permission is required to reuse all or part of the article published by MDPI, including figures and tables. For articles published under an open access Creative Common CC BY license, any part of the article may be reused without permission provided that the original article is clearly cited. For more information, please refer to https://www.mdpi.com/openaccess .
Feature papers represent the most advanced research with significant potential for high impact in the field. A Feature Paper should be a substantial original Article that involves several techniques or approaches, provides an outlook for future research directions and describes possible research applications.
Feature papers are submitted upon individual invitation or recommendation by the scientific editors and must receive positive feedback from the reviewers.
Editor’s Choice articles are based on recommendations by the scientific editors of MDPI journals from around the world. Editors select a small number of articles recently published in the journal that they believe will be particularly interesting to readers, or important in the respective research area. The aim is to provide a snapshot of some of the most exciting work published in the various research areas of the journal.
Original Submission Date Received: .
- Active Journals
- Find a Journal
- Proceedings Series
- For Authors
- For Reviewers
- For Editors
- For Librarians
- For Publishers
- For Societies
- For Conference Organizers
- Open Access Policy
- Institutional Open Access Program
- Special Issues Guidelines
- Editorial Process
- Research and Publication Ethics
- Article Processing Charges
- Testimonials
- Preprints.org
- SciProfiles
- Encyclopedia

Article Menu

- Subscribe SciFeed
- Recommended Articles
- Author Biographies
- Google Scholar
- on Google Scholar
- Table of Contents
Find support for a specific problem in the support section of our website.
Please let us know what you think of our products and services.
Visit our dedicated information section to learn more about MDPI.
JSmol Viewer
Deep learning-based real-time 6d pose estimation and multi-mode tracking algorithms for citrus-harvesting robots.

1. Introduction
2. related work, 2.1. camera calibration, 2.2. 3d model extraction, 2.3. deep learning model, 2.4. object labeling based on driving and harvesting mode, 3. proposed method, 3.1. building a dataset, 3.2. deep learning model architecture, 3.3. object labeling and tracking according to the driving and harvesting mode, 4. experimental results, 5. discussion, 6. conclusions, author contributions, data availability statement, conflicts of interest.
- Rad, M.; Lepetit, V. Bb8: A scalable, accurate, robust to partial occlusion method for predicting the 3d poses of challenging objects without using depth. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3828–3836. [ Google Scholar ]
- Lin, K.-Y.; Tseng, Y.-H.; Chiang, K.-W. Interpretation and transformation of intrinsic camera parameters used in photogrammetry and computer vision. Sensors 2022 , 22 , 9602. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Szeliski, R. Computer Vision: Algorithms and Applications ; Springer Nature: Berlin/Heidelberg, Germany, 2022. [ Google Scholar ]
- Onishi, Y.; Yoshida, T.; Kurita, H.; Fukao, T.; Arihara, H.; Iwai, A. An automated fruit harvesting robot by using deep learning. Robomech J. 2019 , 6 , 13. [ Google Scholar ] [ CrossRef ]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part I 14. pp. 21–37. [ Google Scholar ]
- Yu, Y.; Zhang, K.; Liu, H.; Yang, L.; Zhang, D. Real-time visual localization of the picking points for a ridge-planting strawberry harvesting robot. IEEE Access 2020 , 8 , 116556–116568. [ Google Scholar ] [ CrossRef ]
- Farhadi, A.; Redmon, J. Yolov3: An incremental improvement. In Proceedings of the Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1–6. [ Google Scholar ]
- Santos, T.T.; De Souza, L.L.; dos Santos, A.A.; Avila, S. Grape detection, segmentation, and tracking using deep neural networks and three-dimensional association. Comput. Electron. Agric. 2020 , 170 , 105247. [ Google Scholar ] [ CrossRef ]
- Jia, W.; Tian, Y.; Luo, R.; Zhang, Z.; Lian, J.; Zheng, Y. Detection and segmentation of overlapped fruits based on optimized mask R-CNN application in apple harvesting robot. Comput. Electron. Agric. 2020 , 172 , 105380. [ Google Scholar ] [ CrossRef ]
- Afonso, M.; Fonteijn, H.; Fiorentin, F.S.; Lensink, D.; Mooij, M.; Faber, N.; Polder, G.; Wehrens, R. Tomato fruit detection and counting in greenhouses using deep learning. Front. Plant Sci. 2020 , 11 , 571299. [ Google Scholar ] [ CrossRef ]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [ Google Scholar ]
- Song, S.; Yu, F.; Zeng, A.; Chang, A.X.; Savva, M.; Funkhouser, T. Semantic scene completion from a single depth image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1746–1754. [ Google Scholar ]
- Brito, A. Blender 3D ; Novatec: New York, NY, USA, 2007. [ Google Scholar ]
- Hodan, T.; Michel, F.; Brachmann, E.; Kehl, W.; GlentBuch, A.; Kraft, D.; Drost, B.; Vidal, J.; Ihrke, S.; Zabulis, X. Bop: Benchmark for 6d object pose estimation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 19–34. [ Google Scholar ]
- Bukschat, Y.; Vetter, M. EfficientPose: An efficient, accurate and scalable end-to-end 6D multi object pose estimation approach. arXiv 2020 , arXiv:2011.04307. [ Google Scholar ]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [ Google Scholar ]
- Tan, M.; Pang, R.; Le, Q.V. Efficientdet: Scalable and efficient object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 10781–10790. [ Google Scholar ]
- Xiang, Y.; Schmidt, T.; Narayanan, V.; Fox, D. Posecnn: A convolutional neural network for 6d object pose estimation in cluttered scenes. arXiv 2017 , arXiv:1711.00199. [ Google Scholar ]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. Mar. 1960 , 82 , 35–45. [ Google Scholar ] [ CrossRef ]
- Bewley, A.; Ge, Z.; Ott, L.; Ramos, F.; Upcroft, B. Simple online and realtime tracking. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 3464–3468. [ Google Scholar ]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955 , 2 , 83–97. [ Google Scholar ] [ CrossRef ]
- Dokmanic, I.; Parhizkar, R.; Ranieri, J.; Vetterli, M. Euclidean distance matrices: Essential theory, algorithms, and applications. IEEE Signal Process. Mag. 2015 , 32 , 12–30. [ Google Scholar ] [ CrossRef ]
- Denninger, M.; Sundermeyer, M.; Winkelbauer, D.; Zidan, Y.; Olefir, D.; Elbadrawy, M.; Lodhi, A.; Katam, H. Blenderproc. arXiv 2019 , arXiv:1911.01911. [ Google Scholar ]
- Lee, D.H.; Lee, S.S.; Kang, H.H.; Ahn, C.K. Camera position estimation for UAVs using SolvePnP with Kalman filter. In Proceedings of the 2018 1st IEEE International Conference on Hot Information-Centric Networking (HotICN), Shenzhen, China, 15–17 August 2018; pp. 250–251. [ Google Scholar ]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017 , arXiv:1704.04861. [ Google Scholar ]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.-C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [ Google Scholar ]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [ Google Scholar ]
- Viviers, C.G.; Filatova, L.; Termeer, M.; de With, P.H.; van der Sommen, F. Advancing 6-DoF Instrument Pose Estimation in Variable X-Ray Imaging Geometries. IEEE Trans. Image Process. 2024 , 33 , 2462–2476. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Hinterstoisser, S.; Lepetit, V.; Ilic, S.; Holzer, S.; Bradski, G.; Konolige, K.; Navab, N. Model based training, detection and pose estimation of texture-less 3d objects in heavily cluttered scenes. In Proceedings of the Computer Vision–ACCV 2012: 11th Asian Conference on Computer Vision, Daejeon, Republic of Korea, 5–9 November 2012; Revised Selected Papers, Part I 11. pp. 548–562. [ Google Scholar ]
- Liu, Y.; Zhai, G.; Zhao, D.; Liu, X. Frame rate and perceptual quality for HD video. In Proceedings of the Advances in Multimedia Information Processing—PCM 2015: 16th Pacific-Rim Conference on Multimedia, Gwangju, Republic of Korea, 16–18 September 2015; Proceedings, Part II 16. pp. 497–505. [ Google Scholar ]
- Düntsch, I.; Gediga, G. Confusion matrices and rough set data analysis. J. Phys. Conf. Ser. 2019 , 1229 , 012055. [ Google Scholar ] [ CrossRef ]
Click here to enlarge figure
| Method | YOLOv5-6D | EfficientPose ( = 0) |
|---|---|---|
| Red | 97.87 | 98.25 |
| Green | 95.15 | 96.98 |
| Average | 96.51 | 97.615 |
| Scene | TP | FN | FP | TN |
|---|---|---|---|---|
| 1 | 100 | 0 | 100 | 0 |
| 2 | 100 | 0 | 50 | 50 |
| 3 | 100 | 0 | 100 | 0 |
| 4 | 100 | 0 | 100 | 0 |
| 5 | 75 | 25 | 100 | 0 |
| 6 | 100 | 0 | 100 | 0 |
| 7 | 100 | 0 | 100 | 0 |
| 8 | 100 | 0 | 100 | 0 |
| 9 | 100 | 0 | 100 | 0 |
| 10 | 100 | 0 | 100 | 0 |
| Recognition rate (%) | 97.5 | 2.5 | 95 | 5 |
| The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
Share and Cite
Hwang, H.-J.; Cho, J.-H.; Kim, Y.-T. Deep Learning-Based Real-Time 6D Pose Estimation and Multi-Mode Tracking Algorithms for Citrus-Harvesting Robots. Machines 2024 , 12 , 642. https://doi.org/10.3390/machines12090642
Hwang H-J, Cho J-H, Kim Y-T. Deep Learning-Based Real-Time 6D Pose Estimation and Multi-Mode Tracking Algorithms for Citrus-Harvesting Robots. Machines . 2024; 12(9):642. https://doi.org/10.3390/machines12090642
Hwang, Hyun-Jung, Jae-Hoon Cho, and Yong-Tae Kim. 2024. "Deep Learning-Based Real-Time 6D Pose Estimation and Multi-Mode Tracking Algorithms for Citrus-Harvesting Robots" Machines 12, no. 9: 642. https://doi.org/10.3390/machines12090642
Article Metrics
Article access statistics, further information, mdpi initiatives, follow mdpi.

Subscribe to receive issue release notifications and newsletters from MDPI journals

IMAGES
VIDEO
COMMENTS
The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term "Hungarian method" to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let's go through the steps of the Hungarian method with the help of a solved example.
The Hungarian algorithm, aka Munkres assignment algorithm, utilizes the following theorem for polynomial runtime complexity (worst case O(n 3)) and guaranteed optimality: If a number is added to or subtracted from all of the entries of any one row or column of a cost matrix, then an optimal assignment for the resulting cost matrix is also an ...
The Hungarian method is a combinatorial optimization algorithm that solves the assignment problem in polynomial time and which anticipated later primal-dual methods.It was developed and published in 1955 by Harold Kuhn, who gave it the name "Hungarian method" because the algorithm was largely based on the earlier works of two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry.
The Hungarian Algorithm is a powerful method used to solve the assignment problem, which involves finding the optimal assignment of a set of tasks to a set of resources. This algorithm, also known as the Munkres Algorithm or the Kuhn-Munkres Algorithm, was developed by two mathematicians, Harold Kuhn and James Munkres, in the 1950s.
1. INTRODUCTION The Hungarian Method [ 11 is an algorithm for solving assignment problems that is based on the work of D. Konig and J. Egervgry. In one possible interpretation, an assignment problem asks for the best assignment of a set of persons to a set of jobs, where the feasible assignments are ranked by the total scores or ratings of the ...
The Hungarian method is a combinatorial optimization algorithm which solves the assignment problem in polynomial time . Later it was discovered that it was a primal-dual Simplex method.. It was developed and published by Harold Kuhn in 1955, who gave the name "Hungarian method" because the algorithm was largely based on the earlier works of two Hungarian mathematicians: Denes Konig and Jeno ...
In this lesson we learn what is an assignment problem and how we can solve it using the Hungarian method.
General description of the algorithm. This problem is known as the assignment problem. The assignment problem is a special case of the transportation problem, which in turn is a special case of the min-cost flow problem, so it can be solved using algorithms that solve the more general cases. Also, our problem is a special case of binary integer ...
This process is experimental and the keywords may be updated as the learning algorithm improves. ... On the origin of the Hungarian Method, History of mathematical programming; a collection of personal reminiscences (J.K ... H.W. (2010). The Hungarian Method for the Assignment Problem. In: Jünger, M., et al. 50 Years of Integer Programming ...
The Hungarian algorithm is used to solve this problem every time we book a Uber or Ola. The assignment problem is best represented as a bipartite graph, which is a graph with two distinct set of nodes, and the edges never connect nodes from the same set. We take the taxi matching example, and the bipartite graph here shows the possible ...
A note on Hungarian method for solving assignment problem. Jayanta Dutta Subhas Chandra Pal. Computer Science, Mathematics. 2015. TLDR. Hungarian method is modified to find out the optimal solution of an assignment problem which reduces the computational cost of the method. Expand.
84. THE HUNGARIAN METHOD FOR THE ASSIGNMENT PROBLEM. 1, 2, and 3. 3 and 4. This information can be presented effectively by a qualification matrix. in which horizontal rows stand for individuals and vertical columns for jobs; a qualified individ- ual is marked by a 1 and an unqualified individual by a 0.
For implementing the above algorithm, the idea is to use the max_cost_assignment() function defined in the dlib library. This function is an implementation of the Hungarian algorithm (also known as the Kuhn-Munkres algorithm) which runs in O(N 3) time. It solves the optimal assignment problem. Below is the implementation of the above approach:
Hungarian Algorithm & Python Code Step by Step. In this section, we will show how to use the Hungarian algorithm to solve linear assignment problems and find the minimum combinations in the matrix. Of course, the Hungarian algorithm can also be used to find the maximum combination. Step 0. Prepare Operations.
The Hungarian Method: The following algorithm applies the above theorem to a given n × n cost matrix to find an optimal assignment. Step 1. Subtract the smallest entry in each row from all the entries of its row. Step 2. Subtract the smallest entry in each column from all the entries of its column. Step 3.
Hungarian Algorithm (also called Kuhn-Munkres Algorithm) Easy to understand, but not for practical applications Successive shortest path algorithm (Hungarian; Jonker, Volgenant and Castanon (JVC)) Signature … Not efficient computationally •Special cases •M-Best Assignment Algorithms Murty (1968) Stone & Cox (1995)
dictionary and taught myself enough Hungarian to translate Egerv´ary's paper. I then realized that Egervary's paper gave a computationally trivial method for reducing´ the general assignment problem to a 0-1 problem. Thus, by putting the two ideas together, the Hungarian Method was born. I tested the algorithm by solving 12 by
Hungarian method for assignment problem is generally used in parallel environment for the assignment of job to a processor. If the number of processors and number of jobs are same, then we can assign each processor 1 job with less cost using Hungarian method. If the...
Solve an assignment problem online. Fill in the cost matrix of an assignment problem and click on 'Solve'. The optimal assignment will be determined and a step by step explanation of the hungarian algorithm will be given. Fill in the cost matrix ():
The assignment problem. The assignment problem deals with assigning machines to tasks, workers to jobs, soccer players to positions, and so on. The goal is to determine the optimum assignment that, for example, minimizes the total cost or maximizes the team effectiveness. Read more on the assignment problem.
It is shown that ideas latent in the work of two Hungarian mathematicians may be exploited to yield a new method of solving this problem. Bibliography 1 König, D. , " Über Graphen und ihre Anwendung auf Determinantentheorie und Mengenlehre.
The Hungarian method is created initially by Kuhn-Munkres to address the linear assignment problem [7] [8] [9]. The basic Hungarian technique is defined to operate with a square or balanced cost ...
The SORT algorithm integrates an object detector, a Kalman filter, I o U distance calculation, and the Hungarian algorithm to enable real-time object tracking. The object detector predicts the position of objects in each frame by generating bounding boxes in the format [ x , y , a , h ] , where x and y represent the center coordinates of the ...