What is The Null Hypothesis & When Do You Reject The Null Hypothesis
Julia Simkus
Editor at Simply Psychology
BA (Hons) Psychology, Princeton University
Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.
Learn about our Editorial Process
Saul McLeod, PhD
Editor-in-Chief for Simply Psychology
BSc (Hons) Psychology, MRes, PhD, University of Manchester
Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.
Olivia Guy-Evans, MSc
Associate Editor for Simply Psychology
BSc (Hons) Psychology, MSc Psychology of Education
Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.
On This Page:
A null hypothesis is a statistical concept suggesting no significant difference or relationship between measured variables. It’s the default assumption unless empirical evidence proves otherwise.
The null hypothesis states no relationship exists between the two variables being studied (i.e., one variable does not affect the other).
The null hypothesis is the statement that a researcher or an investigator wants to disprove.
Testing the null hypothesis can tell you whether your results are due to the effects of manipulating the dependent variable or due to random chance.

How to Write a Null Hypothesis
Null hypotheses (H0) start as research questions that the investigator rephrases as statements indicating no effect or relationship between the independent and dependent variables.
It is a default position that your research aims to challenge or confirm.
For example, if studying the impact of exercise on weight loss, your null hypothesis might be:
There is no significant difference in weight loss between individuals who exercise daily and those who do not.
Examples of Null Hypotheses
| Research Question | Null Hypothesis |
|---|---|
| Do teenagers use cell phones more than adults? | Teenagers and adults use cell phones the same amount. |
| Do tomato plants exhibit a higher rate of growth when planted in compost rather than in soil? | Tomato plants show no difference in growth rates when planted in compost rather than soil. |
| Does daily meditation decrease the incidence of depression? | Daily meditation does not decrease the incidence of depression. |
| Does daily exercise increase test performance? | There is no relationship between daily exercise time and test performance. |
| Does the new vaccine prevent infections? | The vaccine does not affect the infection rate. |
| Does flossing your teeth affect the number of cavities? | Flossing your teeth has no effect on the number of cavities. |
When Do We Reject The Null Hypothesis?
We reject the null hypothesis when the data provide strong enough evidence to conclude that it is likely incorrect. This often occurs when the p-value (probability of observing the data given the null hypothesis is true) is below a predetermined significance level.
If the collected data does not meet the expectation of the null hypothesis, a researcher can conclude that the data lacks sufficient evidence to back up the null hypothesis, and thus the null hypothesis is rejected.
Rejecting the null hypothesis means that a relationship does exist between a set of variables and the effect is statistically significant ( p > 0.05).
If the data collected from the random sample is not statistically significance , then the null hypothesis will be accepted, and the researchers can conclude that there is no relationship between the variables.
You need to perform a statistical test on your data in order to evaluate how consistent it is with the null hypothesis. A p-value is one statistical measurement used to validate a hypothesis against observed data.
Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis.
The level of statistical significance is often expressed as a p -value between 0 and 1. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.

Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01) as general guidelines to decide if you should reject or keep the null.
When your p-value is less than or equal to your significance level, you reject the null hypothesis.
In other words, smaller p-values are taken as stronger evidence against the null hypothesis. Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis.
In this case, the sample data provides insufficient data to conclude that the effect exists in the population.
Because you can never know with complete certainty whether there is an effect in the population, your inferences about a population will sometimes be incorrect.
When you incorrectly reject the null hypothesis, it’s called a type I error. When you incorrectly fail to reject it, it’s called a type II error.
Why Do We Never Accept The Null Hypothesis?
The reason we do not say “accept the null” is because we are always assuming the null hypothesis is true and then conducting a study to see if there is evidence against it. And, even if we don’t find evidence against it, a null hypothesis is not accepted.
A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist.
It is risky to conclude that the null hypothesis is true merely because we did not find evidence to reject it. It is always possible that researchers elsewhere have disproved the null hypothesis, so we cannot accept it as true, but instead, we state that we failed to reject the null.
One can either reject the null hypothesis, or fail to reject it, but can never accept it.
Why Do We Use The Null Hypothesis?
We can never prove with 100% certainty that a hypothesis is true; We can only collect evidence that supports a theory. However, testing a hypothesis can set the stage for rejecting or accepting this hypothesis within a certain confidence level.
The null hypothesis is useful because it can tell us whether the results of our study are due to random chance or the manipulation of a variable (with a certain level of confidence).
A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis.
Rejecting the null hypothesis sets the stage for further experimentation to see if a relationship between two variables exists.
Hypothesis testing is a critical part of the scientific method as it helps decide whether the results of a research study support a particular theory about a given population. Hypothesis testing is a systematic way of backing up researchers’ predictions with statistical analysis.
It helps provide sufficient statistical evidence that either favors or rejects a certain hypothesis about the population parameter.
Purpose of a Null Hypothesis
- The primary purpose of the null hypothesis is to disprove an assumption.
- Whether rejected or accepted, the null hypothesis can help further progress a theory in many scientific cases.
- A null hypothesis can be used to ascertain how consistent the outcomes of multiple studies are.
Do you always need both a Null Hypothesis and an Alternative Hypothesis?
The null (H0) and alternative (Ha or H1) hypotheses are two competing claims that describe the effect of the independent variable on the dependent variable. They are mutually exclusive, which means that only one of the two hypotheses can be true.
While the null hypothesis states that there is no effect in the population, an alternative hypothesis states that there is statistical significance between two variables.
The goal of hypothesis testing is to make inferences about a population based on a sample. In order to undertake hypothesis testing, you must express your research hypothesis as a null and alternative hypothesis. Both hypotheses are required to cover every possible outcome of the study.
What is the difference between a null hypothesis and an alternative hypothesis?
The alternative hypothesis is the complement to the null hypothesis. The null hypothesis states that there is no effect or no relationship between variables, while the alternative hypothesis claims that there is an effect or relationship in the population.
It is the claim that you expect or hope will be true. The null hypothesis and the alternative hypothesis are always mutually exclusive, meaning that only one can be true at a time.
What are some problems with the null hypothesis?
One major problem with the null hypothesis is that researchers typically will assume that accepting the null is a failure of the experiment. However, accepting or rejecting any hypothesis is a positive result. Even if the null is not refuted, the researchers will still learn something new.
Why can a null hypothesis not be accepted?
We can either reject or fail to reject a null hypothesis, but never accept it. If your test fails to detect an effect, this is not proof that the effect doesn’t exist. It just means that your sample did not have enough evidence to conclude that it exists.
We can’t accept a null hypothesis because a lack of evidence does not prove something that does not exist. Instead, we fail to reject it.
Failing to reject the null indicates that the sample did not provide sufficient enough evidence to conclude that an effect exists.
If the p-value is greater than the significance level, then you fail to reject the null hypothesis.
Is a null hypothesis directional or non-directional?
A hypothesis test can either contain an alternative directional hypothesis or a non-directional alternative hypothesis. A directional hypothesis is one that contains the less than (“<“) or greater than (“>”) sign.
A nondirectional hypothesis contains the not equal sign (“≠”). However, a null hypothesis is neither directional nor non-directional.
A null hypothesis is a prediction that there will be no change, relationship, or difference between two variables.
The directional hypothesis or nondirectional hypothesis would then be considered alternative hypotheses to the null hypothesis.
Gill, J. (1999). The insignificance of null hypothesis significance testing. Political research quarterly , 52 (3), 647-674.
Krueger, J. (2001). Null hypothesis significance testing: On the survival of a flawed method. American Psychologist , 56 (1), 16.
Masson, M. E. (2011). A tutorial on a practical Bayesian alternative to null-hypothesis significance testing. Behavior research methods , 43 , 679-690.
Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy. Psychological methods , 5 (2), 241.
Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test. Psychological bulletin , 57 (5), 416.
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Failing to Reject the Null Hypothesis
By Jim Frost 69 Comments
Failing to reject the null hypothesis is an odd way to state that the results of your hypothesis test are not statistically significant. Why the peculiar phrasing? “Fail to reject” sounds like one of those double negatives that writing classes taught you to avoid. What does it mean exactly? There’s an excellent reason for the odd wording!
In this post, learn what it means when you fail to reject the null hypothesis and why that’s the correct wording. While accepting the null hypothesis sounds more straightforward, it is not statistically correct!
Before proceeding, let’s recap some necessary information. In all statistical hypothesis tests, you have the following two hypotheses:
- The null hypothesis states that there is no effect or relationship between the variables.
- The alternative hypothesis states the effect or relationship exists.
We assume that the null hypothesis is correct until we have enough evidence to suggest otherwise.
After you perform a hypothesis test, there are only two possible outcomes.

- When your p-value is greater than your significance level, you fail to reject the null hypothesis. Your results are not significant. You’ll learn more about interpreting this outcome later in this post.
Related posts : Hypothesis Testing Overview and The Null Hypothesis
Why Don’t Statisticians Accept the Null Hypothesis?
To understand why we don’t accept the null, consider the fact that you can’t prove a negative. A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist. It might exist, but your study missed it. That’s a huge difference and it is the reason for the convoluted wording. Let’s look at several analogies.
Species Presumed to be Extinct

Lack of proof doesn’t represent proof that something doesn’t exist!
Criminal Trials

Perhaps the prosecutor conducted a shoddy investigation and missed clues? Or, the defendant successfully covered his tracks? Consequently, the verdict in these cases is “not guilty.” That judgment doesn’t say the defendant is proven innocent, just that there wasn’t enough evidence to move the jury from the default assumption of innocence.
Hypothesis Tests

The hypothesis test assesses the evidence in your sample. If your test fails to detect an effect, it’s not proof that the effect doesn’t exist. It just means your sample contained an insufficient amount of evidence to conclude that it exists. Like the species that were presumed extinct, or the prosecutor who missed clues, the effect might exist in the overall population but not in your particular sample. Consequently, the test results fail to reject the null hypothesis, which is analogous to a “not guilty” verdict in a trial. There just wasn’t enough evidence to move the hypothesis test from the default position that the null is true.
The critical point across these analogies is that a lack of evidence does not prove something does not exist—just that you didn’t find it in your specific investigation. Hence, you never accept the null hypothesis.
Related post : The Significance Level as an Evidentiary Standard
What Does Fail to Reject the Null Hypothesis Mean?
Accepting the null hypothesis would indicate that you’ve proven an effect doesn’t exist. As you’ve seen, that’s not the case at all. You can’t prove a negative! Instead, the strength of your evidence falls short of being able to reject the null. Consequently, we fail to reject it.
Failing to reject the null indicates that our sample did not provide sufficient evidence to conclude that the effect exists. However, at the same time, that lack of evidence doesn’t prove that the effect does not exist. Capturing all that information leads to the convoluted wording!
What are the possible implications of failing to reject the null hypothesis? Let’s work through them.
First, it is possible that the effect truly doesn’t exist in the population, which is why your hypothesis test didn’t detect it in the sample. Makes sense, right? While that is one possibility, it doesn’t end there.
Another possibility is that the effect exists in the population, but the test didn’t detect it for a variety of reasons. These reasons include the following:
- The sample size was too small to detect the effect.
- The variability in the data was too high. The effect exists, but the noise in your data swamped the signal (effect).
- By chance, you collected a fluky sample. When dealing with random samples, chance always plays a role in the results. The luck of the draw might have caused your sample not to reflect an effect that exists in the population.
Notice how studies that collect a small amount of data or low-quality data are likely to miss an effect that exists? These studies had inadequate statistical power to detect the effect. We certainly don’t want to take results from low-quality studies as proof that something doesn’t exist!
However, failing to detect an effect does not necessarily mean a study is low-quality. Random chance in the sampling process can work against even the best research projects!
If you’re learning about hypothesis testing and like the approach I use in my blog, check out my eBook!

Share this:

Reader Interactions
May 8, 2024 at 9:08 am
Thank you very much for explaining the topic. It brings clarity and makes statistics very simple and interesting. Its helping me in the field of Medical Research.
February 26, 2024 at 7:54 pm
Hi Jim, My question is that can I reverse Null hyposthesis and start with Null: µ1 ≠ µ2 ? Then, if I can reject Null, I will end up with µ1=µ2 for mean comparison and this what I am looking for. But isn’t this cheating?
February 26, 2024 at 11:41 pm
That can be done but it requires you to revamp the entire test. Keep in mind that the reason you normally start out with the null equating to no relationship is because the researchers typically want to prove that a relationship or effect exists. This format forces the researchers to collect a substantial amount of high quality data to have a chance at demonstrating that an effect exists. If they collect a small sample and/or poor quality (e.g., noisy or imprecise), then the results default back to the null stating that no effect exists. So, they have to collect good data and work hard to get findings that suggest the effect exists.
There are tests that flip it around as you suggest where the null states that a relationship does exist. For example, researchers perform an equivalency test when they want to show that there is no difference. That the groups are equal. The test is designed such that it requires a good sample size and high quality data to have a chance at proving equivalency. If they have a small sample size and/or poor quality data, the results default back to the groups being unequal, which is not what they want to show.
So, choose the null hypothesis and corresponding analysis based on what you hope to find. Choose the null hypothesis that forces you to work hard to reject it and get the results that you want. It forces you to collect better evidence to make your case and the results default back to what you don’t want if you do a poor job.
I hope that makes sense!
October 13, 2023 at 5:10 am
Really appreciate how you have been able to explain something difficult in very simple terms. Also covering why you can’t accept a null hypothesis – something which I think is frequently missed. Thank you, Jim.
February 22, 2022 at 11:18 am
Hi Jim, I really appreciate your blog, making difficult things sound simple is a great gift.
I have a doubt about the p-value. You said there are two options when it comes to hypothesis tests results . Reject or failing to reject the null, depending on the p-value and your significant level.
But… a P-value of 0,001 means a stronger evidence than a P-value of 0,01? ( both with a significant level of 5%. Or It doesn`t matter, and just every p-Value under your significant level means the same burden of evidence against the null?
I hope I made my point clear. Thanks a lot for your time.
February 23, 2022 at 9:06 pm
There are different schools of thought about this question. The traditional approach is clear cut. Your results are statistically significance when your p-value is less than or equal to your significance level. When the p-value is greater than the significance level, your results are not significant.
However, as you point out, lower p-values indicate stronger evidence against the null hypothesis. I write about this aspect of p-values in several articles, interpreting p-values (near the end) and p-values and reproducibility .
Personally, I consider both aspects. P-values near 0.05 provide weak evidence. Consequently, I’d be willing to say that p-values less than or equal to 0.05 are statistically significant, but when they’re near 0.05, I’d consider it as a preliminary result that requires more research. However, if the p-value is less 0.01, or even better 0.001, then that’s much stronger evidence and I’ll give those results more weight in my evaluation.
If you read those two articles, I think you’ll see what I mean.
January 1, 2022 at 6:00 pm
HI, I have a quick question that you may be able to help me with. I am using SPSS and carrying out a Mann W U Test it says to retain the null hypothesis. The hypothesis is that males are faster than women at completing a task. So is that saying that they are or are not
January 1, 2022 at 8:17 pm
In that case, your sample data provides insufficient evidence to conclude that males are faster. The results do not prove that males and females are the same speed. You just don’t have enough evidence to say males are faster. In this post, I cover the reasons why you can’t prove the null is true.
November 23, 2021 at 5:36 pm
What if I have to prove in my hypothesis that there shouldn’t be any affect of treatment on patients? Can I say that if my null hypothesis is accepted i have got my results (no effect)? I am confused what to do in this situation. As for null hypothesis we always have to write it with some type of equality. What if I want my result to be what i have stated in null hypothesis i.e. no effect? How to write statements in this case? I am using non parametric test, Mann whitney u test
November 27, 2021 at 4:56 pm
You need to perform an equivalence test, which is a special type of procedure when you want to prove that the results are equal. The problem with a regular hypothesis test is that when you fail to reject the null, you’re not proving that they the outcomes are equal. You can fail to reject the null thanks to a small sample size, noisy data, or a small effect size even when the outcomes are truly different at the population level. An equivalence test sets things up so you need strong evidence to really show that two outcomes are equal.
Unfortunately, I don’t have any content for equivalence testing at this point, but you can read an article about it at Wikipedia: Equivalence Test .
August 13, 2021 at 9:41 pm
Great explanation and great analogies! Thanks.
August 11, 2021 at 2:02 am
I got problems with analysis. I did wound healing experiments with drugs treatment (total 9 groups). When I do the 2-way ANOVA in excel, I got the significant results in sample (Drug Treatment) and columns (Day, Timeline) . But I did not get the significantly results in interactions. Can I still reject the null hypothesis and continue the post-hoc test?
Thank you very much.
June 13, 2021 at 4:51 am
Hi Jim, There are so many books covering maths/programming related to statistics/DS, but may be hardly any book to develop an intuitive understanding. Thanks to you for filling up that gap. After statistics, hypothesis-testing, regression, will it be possible for you to write such books on more topics in DS such as trees, deep-learning etc.
I recently started with reading your book on hypothesis testing (just finished the first chapter). I have a question w.r.t the fuel cost example (from first chapter), where a random sample of 25 families (with sample mean 330.6) is taken. To do the hypothesis testing here, we are taking a sampling distribution with a mean of 260. Then based on the p-value and significance level, we find whether to reject or accept the null hypothesis. The entire decision (to accept or reject the null hypothesis) is based on the sampling distribution about which i have the following questions : a) we are assuming that the sampling distribution is normally distributed. what if it has some other distribution, how can we find that ? b) We have assumed that the sampling distribution is normally distributed and then further assumed that its mean is 260 (as required for the hypothesis testing). But we need the standard deviation as well to define the normal distribution, can you please let me know how do we find the standard deviation for the sampling distribution ? Thanks.
April 24, 2021 at 2:25 pm
Maybe its the idea of “Innocent until proven guilty”? Your Null assume the person is not guilty, and your alternative assumes the person is guilty, only when you have enough evidence (finding statistical significance P0.05 you have failed to reject null hypothesis, null stands,implying the person is not guilty. Or, the person remain innocent.. Correct me if you think it’s wrong but this is the way I interpreted.
April 25, 2021 at 5:10 pm
I used the courtroom/trial analogy within this post. Read that for more details. I’d agree with your general take on the issue except when you have enough evidence you actually reject the null, which in the trial means the defendant is found guilty.
April 17, 2021 at 6:10 am
Can regression analysis be done using 5 companies variables for predicting working capital management and profitability positive/negative relationship?
Also, does null hypothesis rejecting means whatsoever is stated in null hypothesis that is false proved through regression analysis?
I have very less knowledge about regression analysis. Please help me, Sir. As I have my project report due on next week. Thanks in advance!
April 18, 2021 at 10:48 pm
Hi Ahmed, yes, regression analysis can be used for the scenario you describe as long as you have the required data.
For more about the null hypothesis in relation to regression analysis, read my post about regression coefficients and their p-values . I describe the null hypothesis in it.
January 26, 2021 at 7:32 pm
With regards to the legal example above. While your explanation makes sense when simplified to this statistical level, from a legal perspective it is not correct. The presumption of innocence means one does not need to be proven innocent. They are innocent. The onus of proof lies with proving they are guilty. So if you can’t prove someones guilt then in fact you must accept the null hypothesis that they are innocent. It’s not a statistical test so a little bit misleading using it an example, although I see why you would.
If it were a statistical test, then we would probably be rather paranoid that everyone is a murderer but they just haven’t been proven to be one yet.
Great article though, a nice simple and thoughtout explanation.
January 26, 2021 at 9:11 pm
It seems like you misread my post. The hypothesis testing/legal analogy is very strong both in making the case and in the result.
In hypothesis testing, the data have to show beyond a reasonable doubt that the alternative hypothesis is true. In a court case, the prosecutor has to present sufficient evidence to show beyond a reasonable doubt that the defendant is guilty.
In terms of the test/case results. When the evidence (data) is insufficient, you fail to reject the null hypothesis but you do not conclude that the data proves the null is true. In a legal case that has insufficient evidence, the jury finds the defendant to be “not guilty” but they do not say that s/he is proven innocent. To your point specifically, it is not accurate to say that “not guilty” is the same as “proven innocent.”
It’s a very strong parallel.
January 9, 2021 at 11:45 am
Just a question, in my research on hypotheses for an assignment, I am finding it difficult to find an exact definition for a hypothesis itself. I know the defintion, but I’m looking for a citable explanation, any ideas?
January 10, 2021 at 1:37 am
To be clear, do you need to come up with a statistical hypothesis? That’s one where you’ll use a particular statistical hypothesis test. If so, I’ll need to know more about what you’re studying, your variables, and the type of hypothesis test you plan to use.
There are also scientific hypotheses that you’ll state in your proposals, study papers, etc. Those are different from statistical hypotheses (although related). However, those are very study area specific and I don’t cover those types on this blog because this is a statistical blog. But, if it’s a statistical hypothesis for a hypothesis test, then let me know the information I mention above and I can help you out!
November 7, 2020 at 8:33 am
Hi, good read, I’m kind of a novice here, so I’m trying to write a research paper, and I’m trying to make a hypothesis. however looking at the literature, there are contradicting results.
researcher A found that there is relationship between X and Y
however, researcher B found that there is no relationship between X and Y
therefore, what is the null hypothesis between X and y? do we choose what we assumed to be correct for our study? or is is somehow related to the alternative hypothesis? I’m confused.
thank you very much for the help.
November 8, 2020 at 12:07 am
Hypotheses for a statistical test are different than a researcher’s hypothesis. When you’re constructing the statistical hypothesis, you don’t need to consider what other researchers have found. Instead, you construct them so that the test only produces statistically significant results (rejecting the null) when your data provides strong evidence. I talk about that process in this post.
Typically, researchers are hoping to establish that an effect or relationship exists. Consequently, the null and alternative hypotheses are typically the following:
Null: The effect or relationship doesn’t not exist. Alternative: The effect or relationship does exist.
However, if you’re hoping to prove that there is no effect or no relationship, you then need to flip those hypotheses and use a special test, such as an equivalences test.
So, there’s no need to consider what researchers have found but instead what you’re looking for. In most cases, you are looking for an effect/relationship, so you’d go with the hypotheses as I show them above.
I hope that helps!
October 22, 2020 at 6:13 pm
Great, deep detailed answer. Appreciated!
September 16, 2020 at 12:03 pm
Thank you for explaining it too clearly. I have the following situation with a Box Bohnken design of three levels and three factors for multiple responses. F-value for second order model is not significant (failing to reject null hypothesis, p-value > 0.05) but, lack of fit of the model is not significant. What can you suggest me about statistical analysis?
September 17, 2020 at 2:42 am
Are your first order effects significant?
You want the lack of fit to be nonsignificant. If it’s significant, that means the model doesn’t fit the data well. So, you’re good there! 🙂
September 14, 2020 at 5:18 pm
thank you for all the explicit explanation on the subject.
However, i still got a question about “accepting the null hypothesis”. from textbook, the p-value is the probability that a statistic would take a value that is as extreme as or more extreme than that actually observed.
so, that’s why when p<0.01 we reject the null hypothesis, because it's too rare (p0.05, i can understand that for most cases we cannot accept the null, for example, if p=0.5, it means that the probability to get a statistic from the distribution is 0.5, which is totally random.
But how about when the p is very close to 1, like p=0.95, or p=0.99999999, can’t we say that the probability that the statistic is not from this distribution is less than 0.05, | or in another way, the probability that the statistic is from the distribution is almost 1. can’t we accept the null in such circumstance?
September 11, 2020 at 12:14 pm
Wow! This is beautifully explained. “Lack of proof doesn’t represent proof that something doesn’t exist!”. This kinda, hit me with such force. Can I then, use the same analogy for many other things in life? LOL! 🙂
H0 = God does not exist; H1 = God does exist; WE fail to reject H0 as there is no evidence.
Thank you sir, this has answered many of my questions, statistically speaking! No pun intended with the above.
September 11, 2020 at 4:58 pm
Hi, LOL, I’m glad it had such meaning for you! I’ll leave the determination about the existence of god up to each person, but in general, yes, I think statistical thinking can be helpful when applied to real life. It is important to realize that lack of proof truly is not proof that something doesn’t exist. But, I also consider other statistical concepts, such as confounders and sampling methodology, to be useful keeping in mind when I’m considering everyday life stuff–even when I’m not statistically analyzing it. Those concepts are generally helpful when trying to figure out what is going on in your life! Are there other alternative explanations? Is what you’re perceiving likely to be biased by something that’s affecting the “data” you can observe? Am I drawing a conclusion based on a large or small sample? How strong is the evidence?
A lot of those concepts are great considerations even when you’re just informally assessing and draw conclusions about things happening in your daily life.
August 13, 2020 at 12:04 am
Dear Jim, thanks for clarifying. absolutely, now it makes sense. the topic is murky but it is good to have your guidance, and be clear. I have not come across an instructor as clear in explaining as you do. Appreciate your direction. Thanks a lot, Geetanjali
August 15, 2020 at 3:48 pm
Hi Geetanjali,
I’m glad my website is helpful! That makes my day hearing that. Thanks so much for writing!
August 12, 2020 at 9:37 am
Hi Jim. I am doing data analyis for my masters thesis and my hypothesis testings were insignificant. And I am ok with that. But there is something bothering me. It is the low reliabilities of the 4-Items sub-scales (.55, .68, .75), though the overall alpha is good (.85). I just wonder if it is affecting my hypothesis testings.
August 11, 2020 at 9:23 pm
Thank you sir for replying, yes sir we it’s a RCT study.. where we did within and between the groups analysis and found p>0.05 in between the groups using Mann Whitney U test. So in such cases if the results comes like this we need to Mention that we failed reject the null hypothesis? Is that correct? Whether it tells that the study is inefficient as we couldn’t accept the alternative hypothesis. Thanks is advance.
August 11, 2020 at 9:43 pm
Hi Saumya, ah, this becomes clearer. When ask statistical questions, please be sure to include all relevant information because the details are extremely important. I didn’t know it was an RCT with a treatment and control group. Yes, given that your p-value is greater than your significance level, you fail to reject the null hypothesis. The results are not significant. The experiment provides insufficient evidence to conclude that the outcome in the treatment group is different than the control group.
By the way, you never accept the alternative hypothesis (or the null). The two options are to either reject the null or fail to reject the null. In your case, you fail to reject the null hypothesis.
I hope this helps!
August 11, 2020 at 9:41 am
Sir, p value is0.05, by which we interpret that both the groups are equally effective. In this case I had to reject the alternative hypothesis/ failed to reject null hypothessis.
August 11, 2020 at 12:37 am
sir, within the group analysis the p value for both the groups is significant (p0.05, by which we interpret that though both the treatments are effective, there in no difference between the efficacy of one over the other.. in other words.. no intervention is superior and both are equally effective.
August 11, 2020 at 2:45 pm
Thanks for the additional details. If I understand correctly, there were separate analyses before that determined each treatment had a statistically significance effect. However, when you compare the two treatments, there difference between them is not statistically significant.
If that’s the case, the interpretation is fairly straightforward. You have evidence that suggests that both treatments are effective. However, you don’t have evidence to conclude that one is better than the other.
August 10, 2020 at 9:26 am
Hi thank you for a wonderful explanation. I have a doubt: My Null hypothesis says: no significant difference between the effect fo A and B treatment Alternative hypothesis: there will be significant difference between the effect of A and B treatment. and my results show that i fail to reject null hypothesis.. Both the treatments were effective, but not significant difference.. how do I interpret this?
August 10, 2020 at 1:32 pm
First, I need to ask you a question. If your p-value is not significant, and so you fail to reject the null, why do you say that the treatment is effective? I can answer you question better after knowing the reason you say that. Thanks!
August 9, 2020 at 9:40 am
Dear Jim, thanks for making stats much more understandable and answering all question so painstakingly. I understand the following on p value and null. If our sample yields a p value of .01, it means that that there is a 1% probability that our kind of sample exists in the population. that is a rare event. So why shouldn’t we accept the HO as the probability of our event was v rare. Pls can you correct me. Thanks, G
August 10, 2020 at 1:53 pm
That’s a great question! They key thing to remember is that p-values are a conditional probability. P-value calculations assume that the null hypothesis is true. So, a p-value of 0.01 indicates that there is a 1% probability of observing your sample results, or more extreme, *IF* the null hypothesis is true.
The kicker is that we don’t whether the null is true or not. But, using this process does limit the likelihood of a false positive to your significance level (alpha). But, we don’t know whether the null is true and you had an unusual sample or whether the null is false. Usually, with a p-value of 0.01, we’d reject the null and conclude it is false.
I hope that answered your question. This topic can be murky and I wasn’t quite clear which part you needed clarification.
August 4, 2020 at 11:16 pm
Thank you for the wonderful explanation. However, I was just curious to know that what if in a particular test, we get a p-value less than the level of significance, leading to evidence against null hypothesis. Is there any possibility that our interpretation of population effect might be wrong due to randomness of samples? Also, how do we conclude whether the evidence is enough for our alternate hypothesis?
August 4, 2020 at 11:55 pm
Hi Abhilash,
Yes, unfortunately, when you’re working with samples, there’s always the possibility that random chance will cause your sample to not represent the population. For information about these errors, read my post about the types of errors in hypothesis testing .
In hypothesis testing, you determine whether your evidence is strong enough to reject the null. You don’t accept the alternative hypothesis. I cover that in my post about interpreting p-values .
August 1, 2020 at 3:50 pm
Hi, I am trying to interpret this phenomenon after my research. The null hypothesis states that “The use of combined drugs A and B does not lower blood pressure when compared to if drug A or B is used singularly”
The alternate hypothesis states: The use of combined drugs A and B lower blood pressure compared to if drug A or B is used singularly.
At the end of the study, majority of the people did not actually combine drugs A and B, rather indicated they either used drug A or drug B but not a combination. I am finding it very difficult to explain this outcome more so that it is a descriptive research. Please how do I go about this? Thanks a lot
June 22, 2020 at 10:01 am
What confuses me is how we set/determine the null hypothesis? For example stating that two sets of data are either no different or have no relationship will give completely different outcomes, so which is correct? Is the null that they are different or the same?
June 22, 2020 at 2:16 pm
Typically, the null states there is no effect/no relationship. That’s true for 99% of hypothesis tests. However, there are some equivalence tests where you are trying to prove that the groups are equal. In that case, the null hypothesis states that groups are not equal.
The null hypothesis is typically what you *don’t* want to find. You have to work hard, design a good experiment, collect good data, and end up with sufficient evidence to favor the alternative hypothesis. Usually in an experiment you want to find an effect. So, usually the null states there is no effect and you have get good evidence to reject that notion.
However, there are a few tests where you actually want to prove something is equal, so you need the null to state that they’re not equal in those cases and then do all the hard work and gather good data to suggest that they are equal. Basically, set up the hypothesis so it takes a good experiment and solid evidence to be able to reject the null and favor the hypothesis that you’re hoping is true.
June 5, 2020 at 11:54 am
Thank you for the explanation. I have one question that. If Null hypothesis is failed to reject than is possible to interpret the analysis further?
June 5, 2020 at 7:36 pm
Hi Mottakin,
Typically, if your result is that you fail to reject the null hypothesis there’s not much further interpretation. You don’t want to be in a situation where you’re endlessly trying new things on a quest for obtaining significant results. That’s data mining.
May 25, 2020 at 7:55 am
I hope all is well. I am enjoying your blog. I am not a statistician, however, I use statistical formulae to provide insight on the direction in which data is going. I have used both the regression analysis and a T-Test. I know that both use a null hypothesis and an alternative hypothesis. Could you please clarity the difference between a regression analysis and a T-Test? Are there conditions where one is a better option than the other?
May 26, 2020 at 9:18 pm
t-Tests compare the means of one or two groups. Regression analysis typically describes the relationships between a set of independent variables and the dependent variables. Interestingly, you can actually use regression analysis to perform a t-test. However, that would be overkill. If you just want to compare the means of one or two groups, use a t-test. Read my post about performing t-tests in Excel to see what they can do. If you have a more complex model than just comparing one or two means, regression might be the way to go. Read my post about when to use regression analysis .
May 12, 2020 at 5:45 pm
This article is really enlightening but there is still some darkness looming around. I see that low p-values mean strong evidence against null hypothesis and finding such a sample is highly unlikely when null hypothesis is true. So , is it OK to say that when p-value is 0.01 , it was very unlikely to have found such a sample but we still found it and hence finding such a sample has not occurred just by chance which leads towards rejection of null hypothesis.
May 12, 2020 at 11:16 pm
That’s mostly correct. I wouldn’t say, “has not occurred by chance.” So, when you get a very low p-value it does mean that you are unlikely to obtain that sample if the null is true. However, once you obtain that result, you don’t know for sure which of the two occurred:
- The effect exists in the population.
- Random chance gave you an unusual sample (i.e., Type I error).
You really don’t know for sure. However, by the decision making results you set about the strength of evidence required to reject the null, you conclude that the effect exists. Just always be aware that it could be a false positive.
That’s all a long way of saying that your sample was unlikely to occur by chance if the null is true.
April 29, 2020 at 11:59 am
Why do we consult the statistical tables to find out the critical values of our test statistics?
April 30, 2020 at 5:05 pm
Statistical tables started back in the “olden days” when computers didn’t exist. You’d calculate the test statistic value for your sample. Then, you’d look in the appropriate table and using the degrees of freedom for your design and find the critical values for the test statistic. If the value of your test statistics exceeded the critical value, your results were statistically significant.
With powerful and readily available computers, researchers could analyze their data and calculate the p-values and compare them directly to the significance level.
I hope that answers your question!
April 15, 2020 at 10:12 am
If we are not able to reject the null hypothesis. What could be the solution?
April 16, 2020 at 11:13 pm
Hi Shazzad,
The first thing to recognize is that failing to reject the null hypothesis might not be an error. If the null hypothesis is false, then the correct outcome is failing to reject the null.
However, if the null hypothesis is false and you fail to reject, it is a type II error, or a false negative. Read my post about types of errors in hypothesis tests for more information.
This type of error can occur for a variety of reasons, including the following:
- Fluky sample. When working with random samples, random error can cause anomalous results purely by chance.
- Sample is too small. Perhaps the sample was too small, which means the test didn’t have enough statistical power to detect the difference.
- Problematic data or sampling methodology. There could be a problem with how you collected the data or your sampling methodology.
There are various other possibilities, but those are several common problems.
April 14, 2020 at 12:19 pm
Thank you so much for this article! I am taking my first Statistics class in college and I have one question about this.
I understand that the default position is that the null is correct, and you explained that (just like a court case), the sample evidence must EXCEED the “evidentiary standard” (which is the significance level) to conclude that an effect/relationship exists. And, if an effect/relationship exists, that means that it’s the alternative hypothesis that “wins” (not sure if that’s the correct way of wording it, but I’m trying to make this as simple as possible in my head!).
But what I don’t understand is that if the P-value is GREATER than the significance value, we fail to reject the null….because shouldn’t a higher P-value, mean that our sample evidence EXCEEDS the evidentiary standard (aka the significance level), and therefore an effect/relationship exists? In my mind it would make more sense to reject the null, because our P-value is higher and therefore we have enough evidence to reject the null.
I hope I worded this in a way that makes sense. Thank you in advance!
April 14, 2020 at 10:42 pm
That’s a great question. The key thing to remember is that higher p-values correspond to weaker evidence against the null hypothesis. A high p-value indicates that your sample is likely (high probability = high p-value) if the null hypothesis is true. Conversely, low p-values represent stronger evidence against the null. You were unlikely (low probability = low p-value) to have collect a sample with the measured characteristics if the null is true.
So, there is negative correlation between p-values and strength of evidence against the null hypothesis. Low p-values indicate stronger evidence. Higher p-value represent weaker evidence.
In a nutshell, you reject the null hypothesis with a low p-value because it indicates your sample data are unusual if the null is true. When it’s unusual enough, you reject the null.
March 5, 2020 at 11:10 am
There is something I am confused about. If our significance level is .05 and our resulting p-value is .02 (thus the strength of our evidence is strong enough to reject the null hypothesis), do we state that we reject the null hypothesis with 95% confidence or 98% confidence?
My guess is our confidence level is 95% since or alpha was .05. But if the strength of our evidence is 98%, why wouldn’t we use that as our stated confidence in our results?
March 5, 2020 at 4:19 pm
Hi Michael,
You’d state that you can reject the null at a significance level of 5% or conversely at the 95% confidence level. A key reason is to avoid cherry picking your results. In other words, you don’t want to choose the significance level based on your results.
Consequently, set the significance level/confidence level before performing your analysis. Then, use those preset levels to determine statistical significance. I always recommend including the exact p-value when you report on statistical significance. Exact p-values do provide information about the strength of evidence against the null.
March 5, 2020 at 9:58 am
Thank you for sharing this knowledge , it is very appropriate in explaining some observations in the study of forest biodiversity.
March 4, 2020 at 2:01 am
Thank you so much. This provides for my research
March 3, 2020 at 7:28 pm
If one couples this with what they call estimated monetary value of risk in risk management, one can take better decisions.
March 3, 2020 at 3:12 pm
Thank you for providing this clear insight.
March 3, 2020 at 3:29 am
Nice article Jim. The risk of such failure obviously reduces when a lower significance level is specified.One benefits most by reading this article in conjunction with your other article “Understanding Significance Levels in Statistics”.
March 3, 2020 at 2:43 am
That’s fine. My question is why doesn’t the numerical value of type 1 error coincide with the significance level in the backdrop that the type 1 error and the significance level are both the same ? I hope you got my question.
March 3, 2020 at 3:30 am
Hi, they are equal. As I indicated, the significance level equals the type I error rate.
March 3, 2020 at 1:27 am
Kindly elighten me on one confusion. We set out our significance level before setting our hypothesis. When we calculate the type 1 error, which happens to be a significance level, the numerical value doesn’t equals (either undermining value comes out or an exceeding value comescout ) our significance level that was preassigned. Why is this so ?
March 3, 2020 at 2:24 am
Hi Ratnadeep,
You’re correct. The significance level (alpha) is the same as the type I error rate. However, you compare the p-value to the significance level. It’s the p-value that can be greater than or less than the significance level.
The significance level is the evidentiary standard. How strong does the evidence in your sample need to be before you can reject the null? The p-value indicates the strength of the evidence that is present in your sample. By comparing the p-value to the significance level, you’re comparing the actual strength of the sample evidence to the evidentiary standard to determine whether your sample evidence is strong enough to conclude that the effect exists in the population.
I write about this in my post about the understanding significance levels . I think that will help answer your questions!
Comments and Questions Cancel reply
What 'Fail to Reject' Means in a Hypothesis Test
Casarsa Guru/Getty Images
- Inferential Statistics
- Statistics Tutorials
- Probability & Games
- Descriptive Statistics
- Applications Of Statistics
- Math Tutorials
- Pre Algebra & Algebra
- Exponential Decay
- Worksheets By Grade
- Ph.D., Mathematics, Purdue University
- M.S., Mathematics, Purdue University
- B.A., Mathematics, Physics, and Chemistry, Anderson University
In statistics , scientists can perform a number of different significance tests to determine if there is a relationship between two phenomena. One of the first they usually perform is a null hypothesis test. In short, the null hypothesis states that there is no meaningful relationship between two measured phenomena. After a performing a test, scientists can:
- Reject the null hypothesis (meaning there is a definite, consequential relationship between the two phenomena), or
- Fail to reject the null hypothesis (meaning the test has not identified a consequential relationship between the two phenomena)
Key Takeaways: The Null Hypothesis
• In a test of significance, the null hypothesis states that there is no meaningful relationship between two measured phenomena.
• By comparing the null hypothesis to an alternative hypothesis, scientists can either reject or fail to reject the null hypothesis.
• The null hypothesis cannot be positively proven. Rather, all that scientists can determine from a test of significance is that the evidence collected does or does not disprove the null hypothesis.
It is important to note that a failure to reject does not mean that the null hypothesis is true—only that the test did not prove it to be false. In some cases, depending on the experiment, a relationship may exist between two phenomena that is not identified by the experiment. In such cases, new experiments must be designed to rule out alternative hypotheses.
Null vs. Alternative Hypothesis
The null hypothesis is considered the default in a scientific experiment . In contrast, an alternative hypothesis is one that claims that there is a meaningful relationship between two phenomena. These two competing hypotheses can be compared by performing a statistical hypothesis test, which determines whether there is a statistically significant relationship between the data.
For example, scientists studying the water quality of a stream may wish to determine whether a certain chemical affects the acidity of the water. The null hypothesis—that the chemical has no effect on the water quality—can be tested by measuring the pH level of two water samples, one of which contains some of the chemical and one of which has been left untouched. If the sample with the added chemical is measurably more or less acidic—as determined through statistical analysis—it is a reason to reject the null hypothesis. If the sample's acidity is unchanged, it is a reason to not reject the null hypothesis.
When scientists design experiments, they attempt to find evidence for the alternative hypothesis. They do not try to prove that the null hypothesis is true. The null hypothesis is assumed to be an accurate statement until contrary evidence proves otherwise. As a result, a test of significance does not produce any evidence pertaining to the truth of the null hypothesis.
Failing to Reject vs. Accept
In an experiment, the null hypothesis and the alternative hypothesis should be carefully formulated such that one and only one of these statements is true. If the collected data supports the alternative hypothesis, then the null hypothesis can be rejected as false. However, if the data does not support the alternative hypothesis, this does not mean that the null hypothesis is true. All it means is that the null hypothesis has not been disproven—hence the term "failure to reject." A "failure to reject" a hypothesis should not be confused with acceptance.
In mathematics, negations are typically formed by simply placing the word “not” in the correct place. Using this convention, tests of significance allow scientists to either reject or not reject the null hypothesis. It sometimes takes a moment to realize that “not rejecting” is not the same as "accepting."
Null Hypothesis Example
In many ways, the philosophy behind a test of significance is similar to that of a trial. At the beginning of the proceedings, when the defendant enters a plea of “not guilty,” it is analogous to the statement of the null hypothesis. While the defendant may indeed be innocent, there is no plea of “innocent” to be formally made in court. The alternative hypothesis of “guilty” is what the prosecutor attempts to demonstrate.
The presumption at the outset of the trial is that the defendant is innocent. In theory, there is no need for the defendant to prove that he or she is innocent. The burden of proof is on the prosecuting attorney, who must marshal enough evidence to convince the jury that the defendant is guilty beyond a reasonable doubt. Likewise, in a test of significance, a scientist can only reject the null hypothesis by providing evidence for the alternative hypothesis.
If there is not enough evidence in a trial to demonstrate guilt, then the defendant is declared “not guilty.” This claim has nothing to do with innocence; it merely reflects the fact that the prosecution failed to provide enough evidence of guilt. In a similar way, a failure to reject the null hypothesis in a significance test does not mean that the null hypothesis is true. It only means that the scientist was unable to provide enough evidence for the alternative hypothesis.
For example, scientists testing the effects of a certain pesticide on crop yields might design an experiment in which some crops are left untreated and others are treated with varying amounts of pesticide. Any result in which the crop yields varied based on pesticide exposure—assuming all other variables are equal—would provide strong evidence for the alternative hypothesis (that the pesticide does affect crop yields). As a result, the scientists would have reason to reject the null hypothesis.
- Type I and Type II Errors in Statistics
- Null Hypothesis and Alternative Hypothesis
- An Example of Chi-Square Test for a Multinomial Experiment
- The Difference Between Type I and Type II Errors in Hypothesis Testing
- What Level of Alpha Determines Statistical Significance?
- What Is the Difference Between Alpha and P-Values?
- How to Find Critical Values with a Chi-Square Table
- The Runs Test for Random Sequences
- An Example of a Hypothesis Test
- What Is ANOVA?
- Example of a Permutation Test
- Degrees of Freedom for Independence of Variables in Two-Way Table
- How to Find Degrees of Freedom in Statistics
- Example of an ANOVA Calculation
- Confidence Intervals: 4 Common Mistakes
- How to Construct a Confidence Interval for a Population Proportion
Hypothesis Testing (cont...)
Hypothesis testing, the null and alternative hypothesis.
In order to undertake hypothesis testing you need to express your research hypothesis as a null and alternative hypothesis. The null hypothesis and alternative hypothesis are statements regarding the differences or effects that occur in the population. You will use your sample to test which statement (i.e., the null hypothesis or alternative hypothesis) is most likely (although technically, you test the evidence against the null hypothesis). So, with respect to our teaching example, the null and alternative hypothesis will reflect statements about all statistics students on graduate management courses.
The null hypothesis is essentially the "devil's advocate" position. That is, it assumes that whatever you are trying to prove did not happen ( hint: it usually states that something equals zero). For example, the two different teaching methods did not result in different exam performances (i.e., zero difference). Another example might be that there is no relationship between anxiety and athletic performance (i.e., the slope is zero). The alternative hypothesis states the opposite and is usually the hypothesis you are trying to prove (e.g., the two different teaching methods did result in different exam performances). Initially, you can state these hypotheses in more general terms (e.g., using terms like "effect", "relationship", etc.), as shown below for the teaching methods example:
| Null Hypotheses (H ): | Undertaking seminar classes has no effect on students' performance. |
| Alternative Hypothesis (H ): | Undertaking seminar class has a positive effect on students' performance. |
Depending on how you want to "summarize" the exam performances will determine how you might want to write a more specific null and alternative hypothesis. For example, you could compare the mean exam performance of each group (i.e., the "seminar" group and the "lectures-only" group). This is what we will demonstrate here, but other options include comparing the distributions , medians , amongst other things. As such, we can state:
| Null Hypotheses (H ): | The mean exam mark for the "seminar" and "lecture-only" teaching methods is the same in the population. |
| Alternative Hypothesis (H ): | The mean exam mark for the "seminar" and "lecture-only" teaching methods is not the same in the population. |
Now that you have identified the null and alternative hypotheses, you need to find evidence and develop a strategy for declaring your "support" for either the null or alternative hypothesis. We can do this using some statistical theory and some arbitrary cut-off points. Both these issues are dealt with next.
Significance levels
The level of statistical significance is often expressed as the so-called p -value . Depending on the statistical test you have chosen, you will calculate a probability (i.e., the p -value) of observing your sample results (or more extreme) given that the null hypothesis is true . Another way of phrasing this is to consider the probability that a difference in a mean score (or other statistic) could have arisen based on the assumption that there really is no difference. Let us consider this statement with respect to our example where we are interested in the difference in mean exam performance between two different teaching methods. If there really is no difference between the two teaching methods in the population (i.e., given that the null hypothesis is true), how likely would it be to see a difference in the mean exam performance between the two teaching methods as large as (or larger than) that which has been observed in your sample?
So, you might get a p -value such as 0.03 (i.e., p = .03). This means that there is a 3% chance of finding a difference as large as (or larger than) the one in your study given that the null hypothesis is true. However, you want to know whether this is "statistically significant". Typically, if there was a 5% or less chance (5 times in 100 or less) that the difference in the mean exam performance between the two teaching methods (or whatever statistic you are using) is as different as observed given the null hypothesis is true, you would reject the null hypothesis and accept the alternative hypothesis. Alternately, if the chance was greater than 5% (5 times in 100 or more), you would fail to reject the null hypothesis and would not accept the alternative hypothesis. As such, in this example where p = .03, we would reject the null hypothesis and accept the alternative hypothesis. We reject it because at a significance level of 0.03 (i.e., less than a 5% chance), the result we obtained could happen too frequently for us to be confident that it was the two teaching methods that had an effect on exam performance.
Whilst there is relatively little justification why a significance level of 0.05 is used rather than 0.01 or 0.10, for example, it is widely used in academic research. However, if you want to be particularly confident in your results, you can set a more stringent level of 0.01 (a 1% chance or less; 1 in 100 chance or less).

One- and two-tailed predictions
When considering whether we reject the null hypothesis and accept the alternative hypothesis, we need to consider the direction of the alternative hypothesis statement. For example, the alternative hypothesis that was stated earlier is:
| Alternative Hypothesis (H ): | Undertaking seminar classes has a positive effect on students' performance. |
The alternative hypothesis tells us two things. First, what predictions did we make about the effect of the independent variable(s) on the dependent variable(s)? Second, what was the predicted direction of this effect? Let's use our example to highlight these two points.
Sarah predicted that her teaching method (independent variable: teaching method), whereby she not only required her students to attend lectures, but also seminars, would have a positive effect (that is, increased) students' performance (dependent variable: exam marks). If an alternative hypothesis has a direction (and this is how you want to test it), the hypothesis is one-tailed. That is, it predicts direction of the effect. If the alternative hypothesis has stated that the effect was expected to be negative, this is also a one-tailed hypothesis.
Alternatively, a two-tailed prediction means that we do not make a choice over the direction that the effect of the experiment takes. Rather, it simply implies that the effect could be negative or positive. If Sarah had made a two-tailed prediction, the alternative hypothesis might have been:
| Alternative Hypothesis (H ): | Undertaking seminar classes has an effect on students' performance. |
In other words, we simply take out the word "positive", which implies the direction of our effect. In our example, making a two-tailed prediction may seem strange. After all, it would be logical to expect that "extra" tuition (going to seminar classes as well as lectures) would either have a positive effect on students' performance or no effect at all, but certainly not a negative effect. However, this is just our opinion (and hope) and certainly does not mean that we will get the effect we expect. Generally speaking, making a one-tail prediction (i.e., and testing for it this way) is frowned upon as it usually reflects the hope of a researcher rather than any certainty that it will happen. Notable exceptions to this rule are when there is only one possible way in which a change could occur. This can happen, for example, when biological activity/presence in measured. That is, a protein might be "dormant" and the stimulus you are using can only possibly "wake it up" (i.e., it cannot possibly reduce the activity of a "dormant" protein). In addition, for some statistical tests, one-tailed tests are not possible.
Rejecting or failing to reject the null hypothesis
Let's return finally to the question of whether we reject or fail to reject the null hypothesis.
If our statistical analysis shows that the significance level is below the cut-off value we have set (e.g., either 0.05 or 0.01), we reject the null hypothesis and accept the alternative hypothesis. Alternatively, if the significance level is above the cut-off value, we fail to reject the null hypothesis and cannot accept the alternative hypothesis. You should note that you cannot accept the null hypothesis, but only find evidence against it.
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
- Null and Alternative Hypotheses | Definitions & Examples
Null & Alternative Hypotheses | Definitions, Templates & Examples
Published on May 6, 2022 by Shaun Turney . Revised on June 22, 2023.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :
- Null hypothesis ( H 0 ): There’s no effect in the population .
- Alternative hypothesis ( H a or H 1 ) : There’s an effect in the population.
Table of contents
Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, similarities and differences between null and alternative hypotheses, how to write null and alternative hypotheses, other interesting articles, frequently asked questions.
The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”:
- The null hypothesis ( H 0 ) answers “No, there’s no effect in the population.”
- The alternative hypothesis ( H a ) answers “Yes, there is an effect in the population.”
The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample. It’s critical for your research to write strong hypotheses .
You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example

The null hypothesis is the claim that there’s no effect in the population.
If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.
Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept . Be careful not to say you “prove” or “accept” the null hypothesis.
Null hypotheses often include phrases such as “no effect,” “no difference,” or “no relationship.” When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).
You can never know with complete certainty whether there is an effect in the population. Some percentage of the time, your inference about the population will be incorrect. When you incorrectly reject the null hypothesis, it’s called a type I error . When you incorrectly fail to reject it, it’s a type II error.
Examples of null hypotheses
The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.
| ( ) | ||
| Does tooth flossing affect the number of cavities? | Tooth flossing has on the number of cavities. | test: The mean number of cavities per person does not differ between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ = µ . |
| Does the amount of text highlighted in the textbook affect exam scores? | The amount of text highlighted in the textbook has on exam scores. | : There is no relationship between the amount of text highlighted and exam scores in the population; β = 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression.* | test: The proportion of people with depression in the daily-meditation group ( ) is greater than or equal to the no-meditation group ( ) in the population; ≥ . |
*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .
The alternative hypothesis ( H a ) is the other answer to your research question . It claims that there’s an effect in the population.
Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.
The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.
Alternative hypotheses often include phrases such as “an effect,” “a difference,” or “a relationship.” When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes < or >). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.
Examples of alternative hypotheses
The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.
| Does tooth flossing affect the number of cavities? | Tooth flossing has an on the number of cavities. | test: The mean number of cavities per person differs between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ ≠ µ . |
| Does the amount of text highlighted in a textbook affect exam scores? | The amount of text highlighted in the textbook has an on exam scores. | : There is a relationship between the amount of text highlighted and exam scores in the population; β ≠ 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression. | test: The proportion of people with depression in the daily-meditation group ( ) is less than the no-meditation group ( ) in the population; < . |
Null and alternative hypotheses are similar in some ways:
- They’re both answers to the research question.
- They both make claims about the population.
- They’re both evaluated by statistical tests.
However, there are important differences between the two types of hypotheses, summarized in the following table.
| A claim that there is in the population. | A claim that there is in the population. | |
|
| ||
| Equality symbol (=, ≥, or ≤) | Inequality symbol (≠, <, or >) | |
| Rejected | Supported | |
| Failed to reject | Not supported |
Prevent plagiarism. Run a free check.
To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.
General template sentences
The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:
Does independent variable affect dependent variable ?
- Null hypothesis ( H 0 ): Independent variable does not affect dependent variable.
- Alternative hypothesis ( H a ): Independent variable affects dependent variable.
Test-specific template sentences
Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.
| ( ) | ||
| test
with two groups | The mean dependent variable does not differ between group 1 (µ ) and group 2 (µ ) in the population; µ = µ . | The mean dependent variable differs between group 1 (µ ) and group 2 (µ ) in the population; µ ≠ µ . |
| with three groups | The mean dependent variable does not differ between group 1 (µ ), group 2 (µ ), and group 3 (µ ) in the population; µ = µ = µ . | The mean dependent variable of group 1 (µ ), group 2 (µ ), and group 3 (µ ) are not all equal in the population. |
| There is no correlation between independent variable and dependent variable in the population; ρ = 0. | There is a correlation between independent variable and dependent variable in the population; ρ ≠ 0. | |
| There is no relationship between independent variable and dependent variable in the population; β = 0. | There is a relationship between independent variable and dependent variable in the population; β ≠ 0. | |
| Two-proportions test | The dependent variable expressed as a proportion does not differ between group 1 ( ) and group 2 ( ) in the population; = . | The dependent variable expressed as a proportion differs between group 1 ( ) and group 2 ( ) in the population; ≠ . |
Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).
The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).
A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (“ x affects y because …”).
A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses . In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Turney, S. (2023, June 22). Null & Alternative Hypotheses | Definitions, Templates & Examples. Scribbr. Retrieved September 4, 2024, from https://www.scribbr.com/statistics/null-and-alternative-hypotheses/
Is this article helpful?

Shaun Turney
Other students also liked, inferential statistics | an easy introduction & examples, hypothesis testing | a step-by-step guide with easy examples, type i & type ii errors | differences, examples, visualizations, what is your plagiarism score.

User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
6a.1 - introduction to hypothesis testing, basic terms section .
The first step in hypothesis testing is to set up two competing hypotheses. The hypotheses are the most important aspect. If the hypotheses are incorrect, your conclusion will also be incorrect.
The two hypotheses are named the null hypothesis and the alternative hypothesis.
The goal of hypothesis testing is to see if there is enough evidence against the null hypothesis. In other words, to see if there is enough evidence to reject the null hypothesis. If there is not enough evidence, then we fail to reject the null hypothesis.
Consider the following example where we set up these hypotheses.
Example 6-1 Section
A man, Mr. Orangejuice, goes to trial and is tried for the murder of his ex-wife. He is either guilty or innocent. Set up the null and alternative hypotheses for this example.
Putting this in a hypothesis testing framework, the hypotheses being tested are:
- The man is guilty
- The man is innocent
Let's set up the null and alternative hypotheses.
\(H_0\colon \) Mr. Orangejuice is innocent
\(H_a\colon \) Mr. Orangejuice is guilty
Remember that we assume the null hypothesis is true and try to see if we have evidence against the null. Therefore, it makes sense in this example to assume the man is innocent and test to see if there is evidence that he is guilty.
The Logic of Hypothesis Testing Section
We want to know the answer to a research question. We determine our null and alternative hypotheses. Now it is time to make a decision.
The decision is either going to be...
- reject the null hypothesis or...
- fail to reject the null hypothesis.
Consider the following table. The table shows the decision/conclusion of the hypothesis test and the unknown "reality", or truth. We do not know if the null is true or if it is false. If the null is false and we reject it, then we made the correct decision. If the null hypothesis is true and we fail to reject it, then we made the correct decision.
| Decision | Reality | |
|---|---|---|
| \(H_0\) is true | \(H_0\) is false | |
| Reject \(H_0\), (conclude \(H_a\)) | Correct decision | |
| Fail to reject \(H_0\) | Correct decision | |
So what happens when we do not make the correct decision?
When doing hypothesis testing, two types of mistakes may be made and we call them Type I error and Type II error. If we reject the null hypothesis when it is true, then we made a type I error. If the null hypothesis is false and we failed to reject it, we made another error called a Type II error.
| Decision | Reality | |
|---|---|---|
| \(H_0\) is true | \(H_0\) is false | |
| Reject \(H_0\), (conclude \(H_a\)) | Type I error | Correct decision |
| Fail to reject \(H_0\) | Correct decision | Type II error |
Types of errors
The “reality”, or truth, about the null hypothesis is unknown and therefore we do not know if we have made the correct decision or if we committed an error. We can, however, define the likelihood of these events.
\(\alpha\) and \(\beta\) are probabilities of committing an error so we want these values to be low. However, we cannot decrease both. As \(\alpha\) decreases, \(\beta\) increases.
Example 6-1 Cont'd... Section
A man, Mr. Orangejuice, goes to trial and is tried for the murder of his ex-wife. He is either guilty or not guilty. We found before that...
- \( H_0\colon \) Mr. Orangejuice is innocent
- \( H_a\colon \) Mr. Orangejuice is guilty
Interpret Type I error, \(\alpha \), Type II error, \(\beta \).
As you can see here, the Type I error (putting an innocent man in jail) is the more serious error. Ethically, it is more serious to put an innocent man in jail than to let a guilty man go free. So to minimize the probability of a type I error we would choose a smaller significance level.
Try it! Section
An inspector has to choose between certifying a building as safe or saying that the building is not safe. There are two hypotheses:
- Building is safe
- Building is not safe
Set up the null and alternative hypotheses. Interpret Type I and Type II error.
\( H_0\colon\) Building is not safe vs \(H_a\colon \) Building is safe
| Decision | Reality | |
|---|---|---|
| \(H_0\) is true | \(H_0\) is false | |
| Reject \(H_0\), (conclude \(H_a\)) | Reject "building is not safe" when it is not safe (Type I Error) | Correct decision |
| Fail to reject \(H_0\) | Correct decision | Failing to reject 'building not is safe' when it is safe (Type II Error) |
Power and \(\beta \) are complements of each other. Therefore, they have an inverse relationship, i.e. as one increases, the other decreases.
- Null hypothesis
by Marco Taboga , PhD
In a test of hypothesis , a sample of data is used to decide whether to reject or not to reject a hypothesis about the probability distribution from which the sample was extracted.
The hypothesis is called the null hypothesis, or simply "the null".

Table of contents
The null is like the defendant in a criminal trial
How is the null hypothesis tested, example 1 - proportion of defective items, measurement, test statistic, critical region, interpretation, example 2 - reliability of a production plant, rejection and failure to reject, not rejecting and accepting are not the same thing, failure to reject can be due to lack of power, rejections are easier to interpret, but be careful, takeaways - how to (and not to) formulate a null hypothesis, more examples, more details, best practices in science, keep reading the glossary.
Formulating null hypotheses and subjecting them to statistical testing is one of the workhorses of the scientific method.
Scientists in all fields make conjectures about the phenomena they study, translate them into null hypotheses and gather data to test them.
This process resembles a trial:
the defendant (the null hypothesis) is accused of being guilty (wrong);
evidence (data) is gathered in order to prove the defendant guilty (reject the null);
if there is evidence beyond any reasonable doubt, the defendant is found guilty (the null is rejected);
otherwise, the defendant is found not guilty (the null is not rejected).
Keep this analogy in mind because it helps to better understand statistical tests, their limitations, use and misuse, and frequent misinterpretation.
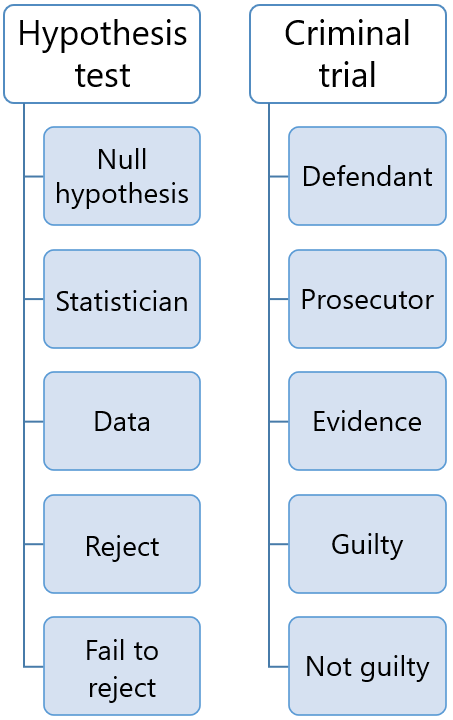
Before collecting the data:
we decide how to summarize the relevant characteristics of the sample data in a single number, the so-called test statistic ;
we derive the probability distribution of the test statistic under the hypothesis that the null is true (the data is regarded as random; therefore, the test statistic is a random variable);
we decide what probability of incorrectly rejecting the null we are willing to tolerate (the level of significance , or size of the test ); the level of significance is typically a small number, such as 5% or 1%.
we choose one or more intervals of values (collectively called rejection region) such that the probability that the test statistic falls within these intervals is equal to the desired level of significance; the rejection region is often a tail of the distribution of the test statistic (one-tailed test) or the union of the left and right tails (two-tailed test).

Then, the data is collected and used to compute the value of the test statistic.
A decision is taken as follows:
if the test statistic falls within the rejection region, then the null hypothesis is rejected;
otherwise, it is not rejected.
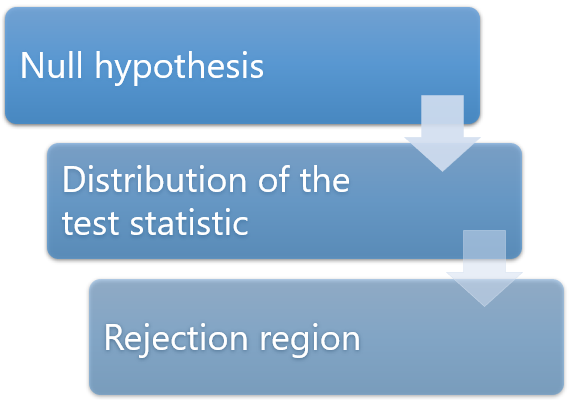
We now make two examples of practical problems that lead to formulate and test a null hypothesis.
A new method is proposed to produce light bulbs.
The proponents claim that it produces less defective bulbs than the method currently in use.
To check the claim, we can set up a statistical test as follows.
We keep the light bulbs on for 10 consecutive days, and then we record whether they are still working at the end of the test period.
The probability that a light bulb produced with the new method is still working at the end of the test period is the same as that of a light bulb produced with the old method.
100 light bulbs are tested:
50 of them are produced with the new method (group A)
the remaining 50 are produced with the old method (group B).
The final data comprises 100 observations of:
an indicator variable which is equal to 1 if the light bulb is still working at the end of the test period and 0 otherwise;
a categorical variable that records the group (A or B) to which each light bulb belongs.
We use the data to compute the proportions of working light bulbs in groups A and B.
The proportions are estimates of the probabilities of not being defective, which are equal for the two groups under the null hypothesis.
We then compute a z-statistic (see here for details) by:
taking the difference between the proportion in group A and the proportion in group B;
standardizing the difference:
we subtract the expected value (which is zero under the null hypothesis);
we divide by the standard deviation (it can be derived analytically).
The distribution of the z-statistic can be approximated by a standard normal distribution .
We decide that the level of confidence must be 5%. In other words, we are going to tolerate a 5% probability of incorrectly rejecting the null hypothesis.
The critical region is the right 5%-tail of the normal distribution, that is, the set of all values greater than 1.645 (see the glossary entry on critical values if you are wondering how this value was obtained).
If the test statistic is greater than 1.645, then the null hypothesis is rejected; otherwise, it is not rejected.
A rejection is interpreted as significant evidence that the new production method produces less defective items; failure to reject is interpreted as insufficient evidence that the new method is better.
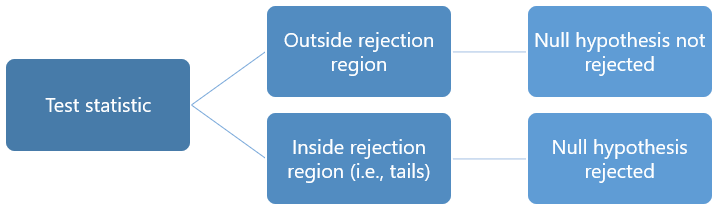
A production plant incurs high costs when production needs to be halted because some machinery fails.
The plant manager has decided that he is not willing to tolerate more than one halt per year on average.
If the expected number of halts per year is greater than 1, he will make new investments in order to improve the reliability of the plant.
A statistical test is set up as follows.
The reliability of the plant is measured by the number of halts.
The number of halts in a year is assumed to have a Poisson distribution with expected value equal to 1 (using the Poisson distribution is common in reliability testing).
The manager cannot wait more than one year before taking a decision.
There will be a single datum at his disposal: the number of halts observed during one year.
The number of halts is used as a test statistic. By assumption, it has a Poisson distribution under the null hypothesis.
The manager decides that the probability of incorrectly rejecting the null can be at most 10%.
A Poisson random variable with expected value equal to 1 takes values:
larger than 1 with probability 26.42%;
larger than 2 with probability 8.03%.
Therefore, it is decided that the critical region will be the set of all values greater than or equal to 3.
If the test statistic is strictly greater than or equal to 3, then the null is rejected; otherwise, it is not rejected.
A rejection is interpreted as significant evidence that the production plant is not reliable enough (the average number of halts per year is significantly larger than tolerated).
Failure to reject is interpreted as insufficient evidence that the plant is unreliable.
This section discusses the main problems that arise in the interpretation of the outcome of a statistical test (reject / not reject).
When the test statistic does not fall within the critical region, then we do not reject the null hypothesis.
Does this mean that we accept the null? Not really.
In general, failure to reject does not constitute, per se, strong evidence that the null hypothesis is true .
Remember the analogy between hypothesis testing and a criminal trial. In a trial, when the defendant is declared not guilty, this does not mean that the defendant is innocent. It only means that there was not enough evidence (not beyond any reasonable doubt) against the defendant.
In turn, lack of evidence can be due:
either to the fact that the defendant is innocent ;
or to the fact that the prosecution has not been able to provide enough evidence against the defendant, even if the latter is guilty .
This is the very reason why courts do not declare defendants innocent, but they use the locution "not guilty".
In a similar fashion, statisticians do not say that the null hypothesis has been accepted, but they say that it has not been rejected.

To better understand why failure to reject does not in general constitute strong evidence that the null hypothesis is true, we need to use the concept of statistical power .
The power of a test is the probability (calculated ex-ante, i.e., before observing the data) that the null will be rejected when another hypothesis (called the alternative hypothesis ) is true.
Let's consider the first of the two examples above (the production of light bulbs).
In that example, the null hypothesis is: the probability that a light bulb is defective does not decrease after introducing a new production method.
Let's make the alternative hypothesis that the probability of being defective is 1% smaller after changing the production process (assume that a 1% decrease is considered a meaningful improvement by engineers).
How much is the ex-ante probability of rejecting the null if the alternative hypothesis is true?
If this probability (the power of the test) is small, then it is very likely that we will not reject the null even if it is wrong.
If we use the analogy with criminal trials, low power means that most likely the prosecution will not be able to provide sufficient evidence, even if the defendant is guilty.
Thus, in the case of lack of power, failure to reject is almost meaningless (it was anyway highly likely).
This is why, before performing a test, it is good statistical practice to compute its power against a relevant alternative .
If the power is found to be too small, there are usually remedies. In particular, statistical power can usually be increased by increasing the sample size (see, e.g., the lecture on hypothesis tests about the mean ).
As we have explained above, interpreting a failure to reject the null hypothesis is not always straightforward. Instead, interpreting a rejection is somewhat easier.
When we reject the null, we know that the data has provided a lot of evidence against the null. In other words, it is unlikely (how unlikely depends on the size of the test) that the null is true given the data we have observed.
There is an important caveat though. The null hypothesis is often made up of several assumptions, including:
the main assumption (the one we are testing);
other assumptions (e.g., technical assumptions) that we need to make in order to set up the hypothesis test.
For instance, in Example 2 above (reliability of a production plant), the main assumption is that the expected number of production halts per year is equal to 1. But there is also a technical assumption: the number of production halts has a Poisson distribution.
It must be kept in mind that a rejection is always a joint rejection of the main assumption and all the other assumptions .
Therefore, we should always ask ourselves whether the null has been rejected because the main assumption is wrong or because the other assumptions are violated.
In the case of Example 2 above, is a rejection of the null due to the fact that the expected number of halts is greater than 1 or is it due to the fact that the distribution of the number of halts is very different from a Poisson distribution?
When we suspect that a rejection is due to the inappropriateness of some technical assumption (e.g., assuming a Poisson distribution in the example), we say that the rejection could be due to misspecification of the model .
The right thing to do when these kind of suspicions arise is to conduct so-called robustness checks , that is, to change the technical assumptions and carry out the test again.
In our example, we could re-run the test by assuming a different probability distribution for the number of halts (e.g., a negative binomial or a compound Poisson - do not worry if you have never heard about these distributions).
If we keep obtaining a rejection of the null even after changing the technical assumptions several times, the we say that our rejection is robust to several different specifications of the model .

What are the main practical implications of everything we have said thus far? How does the theory above help us to set up and test a null hypothesis?
What we said can be summarized in the following guiding principles:
A test of hypothesis is like a criminal trial and you are the prosecutor . You want to find evidence that the defendant (the null hypothesis) is guilty. Your job is not to prove that the defendant is innocent. If you find yourself hoping that the defendant is found not guilty (i.e., the null is not rejected) then something is wrong with the way you set up the test. Remember: you are the prosecutor.
Compute the power of your test against one or more relevant alternative hypotheses. Do not run a test if you know ex-ante that it is unlikely to reject the null when the alternative hypothesis is true.
Beware of technical assumptions that you add to the main assumption you want to test. Make robustness checks in order to verify that the outcome of the test is not biased by model misspecification.
More examples of null hypotheses and how to test them can be found in the following lectures.
| Where the example is found | Null hypothesis |
|---|---|
| The mean of a normal distribution is equal to a certain value | |
| The variance of a normal distribution is equal to a certain value | |
| A vector of parameters estimated by MLE satisfies a set of linear or non-linear restrictions | |
| A regression coefficient is equal to a certain value |
The lecture on Hypothesis testing provides a more detailed mathematical treatment of null hypotheses and how they are tested.
This lecture on the null hypothesis was featured in Stanford University's Best practices in science .

Previous entry: Normal equations
Next entry: Parameter
How to cite
Please cite as:
Taboga, Marco (2021). "Null hypothesis", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/null-hypothesis.
Most of the learning materials found on this website are now available in a traditional textbook format.
- Permutations
- Characteristic function
- Almost sure convergence
- Likelihood ratio test
- Uniform distribution
- Bernoulli distribution
- Multivariate normal distribution
- Chi-square distribution
- Maximum likelihood
- Mathematical tools
- Fundamentals of probability
- Probability distributions
- Asymptotic theory
- Fundamentals of statistics
- About Statlect
- Cookies, privacy and terms of use
- Precision matrix
- Distribution function
- Mean squared error
- IID sequence
- To enhance your privacy,
- we removed the social buttons,
- but don't forget to share .
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
Example 9.1
H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.
Example 9.2
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 66
- H a : μ __ 66
Example 9.3
We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 45
- H a : μ __ 45
Example 9.4
An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066
On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : p __ 0.40
- H a : p __ 0.40
Collaborative Exercise
Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.
Access for free at https://openstax.org/books/statistics/pages/1-introduction
- Authors: Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Statistics
- Publication date: Mar 27, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/statistics/pages/1-introduction
- Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses
© Apr 16, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Rejecting the Null Hypothesis Using Confidence Intervals
- Tech Trends

In an introductory statistics class, there are three main topics that are taught: descriptive statistics and data visualizations, probability and sampling distributions, and statistical inference. Within statistical inference, there are two key methods of statistical inference that are taught, viz. confidence intervals and hypothesis testing . While these two methods are always taught when learning data science and related fields, it is rare that the relationship between these two methods is properly elucidated.
In this article, we’ll begin by defining and describing each method of statistical inference in turn and along the way, state what statistical inference is, and perhaps more importantly, what it isn’t. Then we’ll describe the relationship between the two. While it is typically the case that confidence intervals are taught before hypothesis testing when learning statistics, we’ll begin with the latter since it will allow us to define statistical significance.
Hypothesis Tests
The purpose of a hypothesis test is to answer whether random chance might be responsible for an observed effect. Hypothesis tests use sample statistics to test a hypothesis about population parameters. The null hypothesis, H 0 , is a statement that represents the assumed status quo regarding a variable or variables and it is always about a population characteristic. Some of the ways the null hypothesis is typically glossed are: the population variable is equal to a particular value or there is no difference between the population variables . For example:
- H 0 : μ = 61 in (The mean height of the population of American men is 69 inches)
- H 0 : p 1 -p 2 = 0 (The difference in the population proportions of women who prefer football over baseball and the population proportion of men who prefer football over baseball is 0.)
Note that the null hypothesis always has the equal sign.
The alternative hypothesis, denoted either H 1 or H a , is the statement that is opposed to the null hypothesis (e.g., the population variable is not equal to a particular value or there is a difference between the population variables ):
- H 1 : μ > 61 im (The mean height of the population of American men is greater than 69 inches.)
- H 1 : p 1 -p 2 ≠ 0 (The difference in the population proportions of women who prefer football over baseball and the population proportion of men who prefer football over baseball is not 0.)
The alternative hypothesis is typically the claim that the researcher hopes to show and it always contains the strict inequality symbols (‘<’ left-sided or left-tailed, ‘≠’ two-sided or two-tailed, and ‘>’ right-sided or right-tailed).
When carrying out a test of H 0 vs. H 1 , the null hypothesis H 0 will be rejected in favor of the alternative hypothesis only if the sample provides convincing evidence that H 0 is false. As such, a statistical hypothesis test is only capable of demonstrating strong support for the alternative hypothesis by rejecting the null hypothesis.
When the null hypothesis is not rejected, it does not mean that there is strong support for the null hypothesis (since it was assumed to be true); rather, only that there is not convincing evidence against the null hypothesis. As such, we never use the phrase “accept the null hypothesis.”
In the classical method of performing hypothesis testing, one would have to find what is called the test statistic and use a table to find the corresponding probability. Happily, due to the advancement of technology, one can use Python (as is done in the Flatiron’s Data Science Bootcamp ) and get the required value directly using a Python library like stats models . This is the p-value , which is short for the probability value.
The p-value is a measure of inconsistency between the hypothesized value for a population characteristic and the observed sample. The p -value is the probability, under the assumption the null hypothesis is true, of obtaining a test statistic value that is a measure of inconsistency between the null hypothesis and the data. If the p -value is less than or equal to the probability of the Type I error, then we can reject the null hypothesis and we have sufficient evidence to support the alternative hypothesis.
Typically the probability of a Type I error ɑ, more commonly known as the level of significance , is set to be 0.05, but it is often prudent to have it set to values less than that such as 0.01 or 0.001. Thus, if p -value ≤ ɑ, then we reject the null hypothesis and we interpret this as saying there is a statistically significant difference between the sample and the population. So if the p -value=0.03 ≤ 0.05 = ɑ, then we would reject the null hypothesis and so have statistical significance, whereas if p -value=0.08 ≥ 0.05 = ɑ, then we would fail to reject the null hypothesis and there would not be statistical significance.
Confidence Intervals
The other primary form of statistical inference are confidence intervals. While hypothesis tests are concerned with testing a claim, the purpose of a confidence interval is to estimate an unknown population characteristic. A confidence interval is an interval of plausible values for a population characteristic. They are constructed so that we have a chosen level of confidence that the actual value of the population characteristic will be between the upper and lower endpoints of the open interval.
The structure of an individual confidence interval is the sample estimate of the variable of interest margin of error. The margin of error is the product of a multiplier value and the standard error, s.e., which is based on the standard deviation and the sample size. The multiplier is where the probability, of level of confidence, is introduced into the formula.
The confidence level is the success rate of the method used to construct a confidence interval. A confidence interval estimating the proportion of American men who state they are an avid fan of the NFL could be (0.40, 0.60) with a 95% level of confidence. The level of confidence is not the probability that that population characteristic is in the confidence interval, but rather refers to the method that is used to construct the confidence interval.
For example, a 95% confidence interval would be interpreted as if one constructed 100 confidence intervals, then 95 of them would contain the true population characteristic.
Errors and Power
A Type I error, or a false positive, is the error of finding a difference that is not there, so it is the probability of incorrectly rejecting a true null hypothesis is ɑ, where ɑ is the level of significance. It follows that the probability of correctly failing to reject a true null hypothesis is the complement of it, viz. 1 – ɑ. For a particular hypothesis test, if ɑ = 0.05, then its complement would be 0.95 or 95%.
While we are not going to expand on these ideas, we note the following two related probabilities. A Type II error, or false negative, is the probability of failing to reject a false null hypothesis where the probability of a type II error is β and the power is the probability of correctly rejecting a false null hypothesis where power = 1 – β. In common statistical practice, one typically only speaks of the level of significance and the power.
The following table summarizes these ideas , where the column headers refer to what is actually the case, but is unknown. (If the truth or falsity of the null value was truly known, we wouldn’t have to do statistics.)

Hypothesis Tests and Confidence Intervals
Since hypothesis tests and confidence intervals are both methods of statistical inference, then it is reasonable to wonder if they are equivalent in some way. The answer is yes, which means that we can perform hypothesis testing using confidence intervals.
Returning to the example where we have an estimate of the proportion of American men that are avid fans of the NFL, we had (0.40, 0.60) at a 95% confidence level. As a hypothesis test, we could have the alternative hypothesis as H 1 ≠ 0.51. Since the null value of 0.51 lies within the confidence interval, then we would fail to reject the null hypothesis at ɑ = 0.05.
On the other hand, if H 1 ≠ 0.61, then since 0.61 is not in the confidence interval we can reject the null hypothesis at ɑ = 0.05. Note that the confidence level of 95% and the level of significance at ɑ = 0.05 = 5% are complements, which is the “H o is True” column in the above table.
In general, one can reject the null hypothesis given a null value and a confidence interval for a two-sided test if the null value is not in the confidence interval where the confidence level and level of significance are complements. For one-sided tests, one can still perform a hypothesis test with the confidence level and null value. Not only is there an added layer of complexity for this equivalence, it is the best practice to perform two-sided hypothesis tests since one is not prejudicing the direction of the alternative.
In this discussion of hypothesis testing and confidence intervals, we not only understand when these two methods of statistical inference can be equivalent, but now have a deeper understanding of statistical significance itself and therefore, statistical inference.
Learn More About Data Science at Flatiron
The curriculum in our Data Science Bootcamp incorporates the latest technologies, including artificial intelligence (AI) tools. Download the syllabus to see what you can learn, or book a 10-minute call with Admissions to learn about full-time and part-time attendance opportunities.

About Brendan Patrick Purdy
Brendan is the senior curriculum developer for data science at the Flatiron School. He holds degrees in mathematics, data science, and philosophy, and enjoys modeling neural networks with the Python library TensorFlow.
Related Resources

NYC Campus Tour

Quantifying Rafael Nadal’s Dominance with French Open Data

The Art of Data Exploration
Privacy overview.
| Cookie | Duration | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
5.6 Hypothesis Tests in Depth
Establishing the parameter of interest, type of distribution to use, the test statistic, and p -value can help you figure out how to go about a hypothesis test. However, there are several other factors you should consider when interpreting the results.
Rare Events
Suppose you make an assumption about a property of the population (this assumption is the null hypothesis). Then you gather sample data randomly. If the sample has properties that would be very unlikely to occur if the assumption is true, then you would conclude that your assumption about the population is probably incorrect. Remember that your assumption is just an assumption; it is not a fact, and it may or may not be true. But your sample data are real and are showing you a fact that seems to contradict your assumption.
Errors in Hypothesis Tests
When you perform a hypothesis test, there are four possible outcomes depending on the actual truth (or falseness) of the null hypothesis H 0 and the decision to reject or not. The outcomes are summarized in the following table:
| IS ACTUALLY | ||
|---|---|---|
| Action | ||
| Correct outcome | Type II error | |
| Type I error | Correct outcome | |
The four possible outcomes in the table are:
- The decision is not to reject H 0 when H 0 is true (correct decision).
- The decision is to reject H 0 when H 0 is true (incorrect decision known as a type I error ).
- The decision is not to reject H 0 when, in fact, H 0 is false (incorrect decision known as a type II error ).
- The decision is to reject H 0 when H 0 is false (correct decision whose probability is called the power of the test).
Each of the errors occurs with a particular probability. The Greek letters α and β represent the probabilities.
α = probability of a type I error = P (type I error) = probability of rejecting the null hypothesis when the null hypothesis is true. These are also known as false positives. We know that α is often determined in advance, and α = 0.05 is often widely accepted. In that case, you are saying, “We are OK making this type of error in 5% of samples.” In fact, the p -value is the exact probability of a type I error based on what you observed.
β = probability of a type II error = P (type II error) = probability of not rejecting the null hypothesis when the null hypothesis is false. These are also known as false negatives.
The power of a test is 1 – β .
Ideally, α and β should be as small as possible because they are probabilities of errors but are rarely zero. We want a high power that is as close to one as well. Increasing the sample size can help us achieve these by reducing both α and β and therefore increasing the power of the test.
Suppose the null hypothesis, H 0 , is that Frank’s rock climbing equipment is safe.
Type I error: Frank thinks that his rock climbing equipment may not be safe when, in fact, it really is safe. Type II error: Frank thinks that his rock climbing equipment may be safe when, in fact, it is not safe.
α = probability that Frank thinks his rock climbing equipment may not be safe when, in fact, it really is safe. β = probability that Frank thinks his rock climbing equipment may be safe when, in fact, it is not safe.
Notice that, in this case, the error with the greater consequence is the type II error, in which Frank thinks his rock climbing equipment is safe, so he goes ahead and uses it.
Suppose the null hypothesis, H 0 , is that the blood cultures contain no traces of pathogen X . State the type I and type II errors.
Statistical Significance vs. Practical Significance
When the sample size becomes larger, point estimates become more precise and any real differences in the mean and null value become easier to detect and recognize. Even a very small difference would likely be detected if we took a large enough sample. Sometimes, researchers will take such large samples that even the slightest difference is detected, even differences where there is no practical value. In such cases, we still say the difference is statistically significant , but it is not practically significant.
For example, an online experiment might identify that placing additional ads on a movie review website statistically significantly increases viewership of a TV show by 0.001%, but this increase might not have any practical value.
One role of a data scientist in conducting a study often includes planning the size of the study. The data scientist might first consult experts or scientific literature to learn what would be the smallest meaningful difference from the null value. She also would obtain other information, such as a very rough estimate of the true proportion p , so that she could roughly estimate the standard error. From here, she could suggest a sample size that is sufficiently large enough to detect the real difference if it is meaningful. While larger sample sizes may still be used, these calculations are especially helpful when considering costs or potential risks, such as possible health impacts to volunteers in a medical study.
Click here for more multimedia resources, including podcasts, videos, lecture notes, and worked examples.
The decision is to reject the null hypothesis when, in fact, the null hypothesis is true
Erroneously rejecting a true null hypothesis or erroneously failing to reject a false null hypothesis
The probability of failing to reject a true hypothesis
Finding sufficient evidence that the observed effect is not just due to variability, often from rejecting the null hypothesis
Significant Statistics Copyright © 2024 by John Morgan Russell, OpenStaxCollege, OpenIntro is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Chapter 13: Inferential Statistics
Some Basic Null Hypothesis Tests
Learning Objectives
- Conduct and interpret one-sample, dependent-samples, and independent-samples t tests.
- Interpret the results of one-way, repeated measures, and factorial ANOVAs.
- Conduct and interpret null hypothesis tests of Pearson’s r .
In this section, we look at several common null hypothesis testing procedures. The emphasis here is on providing enough information to allow you to conduct and interpret the most basic versions. In most cases, the online statistical analysis tools mentioned in Chapter 12 will handle the computations—as will programs such as Microsoft Excel and SPSS.
The t Test
As we have seen throughout this book, many studies in psychology focus on the difference between two means. The most common null hypothesis test for this type of statistical relationship is the t test . In this section, we look at three types of t tests that are used for slightly different research designs: the one-sample t test, the dependent-samples t test, and the independent-samples t test.
One-Sample t Test
The one-sample t test is used to compare a sample mean ( M ) with a hypothetical population mean (μ0) that provides some interesting standard of comparison. The null hypothesis is that the mean for the population (µ) is equal to the hypothetical population mean: μ = μ0. The alternative hypothesis is that the mean for the population is different from the hypothetical population mean: μ ≠ μ0. To decide between these two hypotheses, we need to find the probability of obtaining the sample mean (or one more extreme) if the null hypothesis were true. But finding this p value requires first computing a test statistic called t . (A test statistic is a statistic that is computed only to help find the p value.) The formula for t is as follows:
![Rendered by QuickLaTeX.com \[t=\dfrac{M-\mu_0}{\left(\dfrac{SD}{\sqrt{N}}\right)}\]](https://opentextbc.ca/researchmethods/wp-content/ql-cache/quicklatex.com-5cabf5ed8125558a7361164aadc41c78_l3.png)
Again, M is the sample mean and µ 0 is the hypothetical population mean of interest. SD is the sample standard deviation and N is the sample size.
The reason the t statistic (or any test statistic) is useful is that we know how it is distributed when the null hypothesis is true. As shown in Figure 13.1, this distribution is unimodal and symmetrical, and it has a mean of 0. Its precise shape depends on a statistical concept called the degrees of freedom, which for a one-sample t test is N − 1. (There are 24 degrees of freedom for the distribution shown in Figure 13.1.) The important point is that knowing this distribution makes it possible to find the p value for any t score. Consider, for example, a t score of +1.50 based on a sample of 25. The probability of a t score at least this extreme is given by the proportion of t scores in the distribution that are at least this extreme. For now, let us define extreme as being far from zero in either direction. Thus the p value is the proportion of t scores that are +1.50 or above or that are −1.50 or below—a value that turns out to be .14.
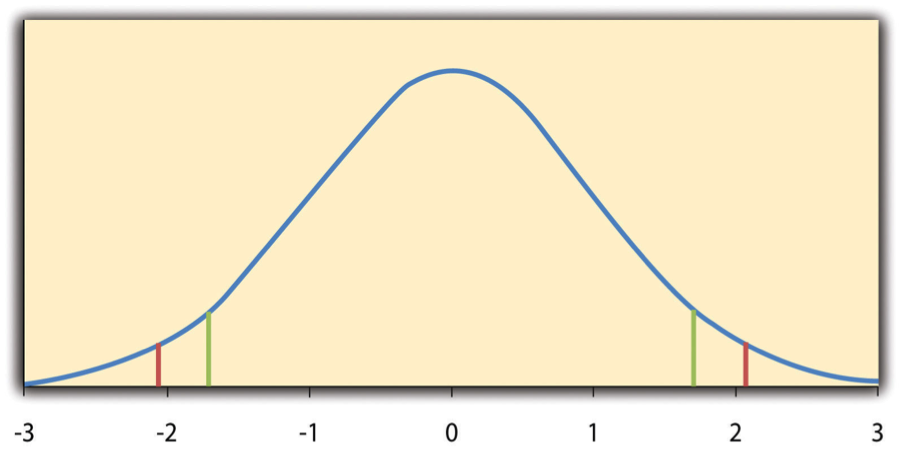
Fortunately, we do not have to deal directly with the distribution of t scores. If we were to enter our sample data and hypothetical mean of interest into one of the online statistical tools in Chapter 12 or into a program like SPSS (Excel does not have a one-sample t test function), the output would include both the t score and the p value. At this point, the rest of the procedure is simple. If p is less than .05, we reject the null hypothesis and conclude that the population mean differs from the hypothetical mean of interest. If p is greater than .05, we retain the null hypothesis and conclude that there is not enough evidence to say that the population mean differs from the hypothetical mean of interest. (Again, technically, we conclude only that we do not have enough evidence to conclude that it does differ.)
If we were to compute the t score by hand, we could use a table like Table 13.2 to make the decision. This table does not provide actual p values. Instead, it provides the critical values of t for different degrees of freedom ( df) when α is .05. For now, let us focus on the two-tailed critical values in the last column of the table. Each of these values should be interpreted as a pair of values: one positive and one negative. For example, the two-tailed critical values when there are 24 degrees of freedom are +2.064 and −2.064. These are represented by the red vertical lines in Figure 13.1. The idea is that any t score below the lower critical value (the left-hand red line in Figure 13.1) is in the lowest 2.5% of the distribution, while any t score above the upper critical value (the right-hand red line) is in the highest 2.5% of the distribution. Therefore any t score beyond the critical value in either direction is in the most extreme 5% of t scores when the null hypothesis is true and has a p value less than .05. Thus if the t score we compute is beyond the critical value in either direction, then we reject the null hypothesis. If the t score we compute is between the upper and lower critical values, then we retain the null hypothesis.
| One-tailed critical value | Two-tailed critical value | |
|---|---|---|
| 3 | 2.353 | 3.182 |
| 4 | 2.132 | 2.776 |
| 5 | 2.015 | 2.571 |
| 6 | 1.943 | 2.447 |
| 7 | 1.895 | 2.365 |
| 8 | 1.860 | 2.306 |
| 9 | 1.833 | 2.262 |
| 10 | 1.812 | 2.228 |
| 11 | 1.796 | 2.201 |
| 12 | 1.782 | 2.179 |
| 13 | 1.771 | 2.160 |
| 14 | 1.761 | 2.145 |
| 15 | 1.753 | 2.131 |
| 16 | 1.746 | 2.120 |
| 17 | 1.740 | 2.110 |
| 18 | 1.734 | 2.101 |
| 19 | 1.729 | 2.093 |
| 20 | 1.725 | 2.086 |
| 21 | 1.721 | 2.080 |
| 22 | 1.717 | 2.074 |
| 23 | 1.714 | 2.069 |
| 24 | 1.711 | 2.064 |
| 25 | 1.708 | 2.060 |
| 30 | 1.697 | 2.042 |
| 35 | 1.690 | 2.030 |
| 40 | 1.684 | 2.021 |
| 45 | 1.679 | 2.014 |
| 50 | 1.676 | 2.009 |
| 60 | 1.671 | 2.000 |
| 70 | 1.667 | 1.994 |
| 80 | 1.664 | 1.990 |
| 90 | 1.662 | 1.987 |
| 100 | 1.660 | 1.984 |
Thus far, we have considered what is called a two-tailed test , where we reject the null hypothesis if the t score for the sample is extreme in either direction. This test makes sense when we believe that the sample mean might differ from the hypothetical population mean but we do not have good reason to expect the difference to go in a particular direction. But it is also possible to do a one-tailed test , where we reject the null hypothesis only if the t score for the sample is extreme in one direction that we specify before collecting the data. This test makes sense when we have good reason to expect the sample mean will differ from the hypothetical population mean in a particular direction.
Here is how it works. Each one-tailed critical value in Table 13.2 can again be interpreted as a pair of values: one positive and one negative. A t score below the lower critical value is in the lowest 5% of the distribution, and a t score above the upper critical value is in the highest 5% of the distribution. For 24 degrees of freedom, these values are −1.711 and +1.711. (These are represented by the green vertical lines in Figure 13.1.) However, for a one-tailed test, we must decide before collecting data whether we expect the sample mean to be lower than the hypothetical population mean, in which case we would use only the lower critical value, or we expect the sample mean to be greater than the hypothetical population mean, in which case we would use only the upper critical value. Notice that we still reject the null hypothesis when the t score for our sample is in the most extreme 5% of the t scores we would expect if the null hypothesis were true—so α remains at .05. We have simply redefined extreme to refer only to one tail of the distribution. The advantage of the one-tailed test is that critical values are less extreme. If the sample mean differs from the hypothetical population mean in the expected direction, then we have a better chance of rejecting the null hypothesis. The disadvantage is that if the sample mean differs from the hypothetical population mean in the unexpected direction, then there is no chance at all of rejecting the null hypothesis.
Example One-Sample t Test
Imagine that a health psychologist is interested in the accuracy of university students’ estimates of the number of calories in a chocolate chip cookie. He shows the cookie to a sample of 10 students and asks each one to estimate the number of calories in it. Because the actual number of calories in the cookie is 250, this is the hypothetical population mean of interest (µ 0 ). The null hypothesis is that the mean estimate for the population (μ) is 250. Because he has no real sense of whether the students will underestimate or overestimate the number of calories, he decides to do a two-tailed test. Now imagine further that the participants’ actual estimates are as follows:
250, 280, 200, 150, 175, 200, 200, 220, 180, 250
The mean estimate for the sample ( M ) is 212.00 calories and the standard deviation ( SD ) is 39.17. The health psychologist can now compute the t score for his sample:
![Rendered by QuickLaTeX.com \[t=\dfrac{212-250}{\left(\dfrac{39.17}{\sqrt{10}}\right)}=-3.07\]](https://opentextbc.ca/researchmethods/wp-content/ql-cache/quicklatex.com-db8519a8464a24c9b7486a9cbd7fdc6b_l3.png)
If he enters the data into one of the online analysis tools or uses SPSS, it would also tell him that the two-tailed p value for this t score (with 10 − 1 = 9 degrees of freedom) is .013. Because this is less than .05, the health psychologist would reject the null hypothesis and conclude that university students tend to underestimate the number of calories in a chocolate chip cookie. If he computes the t score by hand, he could look at Table 13.2 and see that the critical value of t for a two-tailed test with 9 degrees of freedom is ±2.262. The fact that his t score was more extreme than this critical value would tell him that his p value is less than .05 and that he should reject the null hypothesis.
Finally, if this researcher had gone into this study with good reason to expect that university students underestimate the number of calories, then he could have done a one-tailed test instead of a two-tailed test. The only thing this decision would change is the critical value, which would be −1.833. This slightly less extreme value would make it a bit easier to reject the null hypothesis. However, if it turned out that university students overestimate the number of calories—no matter how much they overestimate it—the researcher would not have been able to reject the null hypothesis.

The Dependent-Samples t Test
The dependent-samples t test (sometimes called the paired-samples t test) is used to compare two means for the same sample tested at two different times or under two different conditions. This comparison is appropriate for pretest-posttest designs or within-subjects experiments. The null hypothesis is that the means at the two times or under the two conditions are the same in the population. The alternative hypothesis is that they are not the same. This test can also be one-tailed if the researcher has good reason to expect the difference goes in a particular direction.
It helps to think of the dependent-samples t test as a special case of the one-sample t test. However, the first step in the dependent-samples t test is to reduce the two scores for each participant to a single difference score by taking the difference between them. At this point, the dependent-samples t test becomes a one-sample t test on the difference scores. The hypothetical population mean (µ 0 ) of interest is 0 because this is what the mean difference score would be if there were no difference on average between the two times or two conditions. We can now think of the null hypothesis as being that the mean difference score in the population is 0 (µ 0 = 0) and the alternative hypothesis as being that the mean difference score in the population is not 0 (µ 0 ≠ 0).
Example Dependent-Samples t Test
Imagine that the health psychologist now knows that people tend to underestimate the number of calories in junk food and has developed a short training program to improve their estimates. To test the effectiveness of this program, he conducts a pretest-posttest study in which 10 participants estimate the number of calories in a chocolate chip cookie before the training program and then again afterward. Because he expects the program to increase the participants’ estimates, he decides to do a one-tailed test. Now imagine further that the pretest estimates are
230, 250, 280, 175, 150, 200, 180, 210, 220, 190
and that the posttest estimates (for the same participants in the same order) are
250, 260, 250, 200, 160, 200, 200, 180, 230, 240
The difference scores, then, are as follows:
+20, +10, −30, +25, +10, 0, +20, −30, +10, +50
Note that it does not matter whether the first set of scores is subtracted from the second or the second from the first as long as it is done the same way for all participants. In this example, it makes sense to subtract the pretest estimates from the posttest estimates so that positive difference scores mean that the estimates went up after the training and negative difference scores mean the estimates went down.
The mean of the difference scores is 8.50 with a standard deviation of 27.27. The health psychologist can now compute the t score for his sample as follows:
![Rendered by QuickLaTeX.com \[t=\dfrac{8.5-0}{\left(\dfrac{27.27}{\sqrt{10}}\right)}=1.11\]](https://opentextbc.ca/researchmethods/wp-content/ql-cache/quicklatex.com-37d0f432a138ce195614d7cebaabb4d8_l3.png)
If he enters the data into one of the online analysis tools or uses Excel or SPSS, it would tell him that the one-tailed p value for this t score (again with 10 − 1 = 9 degrees of freedom) is .148. Because this is greater than .05, he would retain the null hypothesis and conclude that the training program does not increase people’s calorie estimates. If he were to compute the t score by hand, he could look at Table 13.2 and see that the critical value of t for a one-tailed test with 9 degrees of freedom is +1.833. (It is positive this time because he was expecting a positive mean difference score.) The fact that his t score was less extreme than this critical value would tell him that his p value is greater than .05 and that he should fail to reject the null hypothesis.
The Independent-Samples t Test
The independent-samples t test is used to compare the means of two separate samples ( M 1 and M 2 ). The two samples might have been tested under different conditions in a between-subjects experiment, or they could be preexisting groups in a correlational design (e.g., women and men, extraverts and introverts). The null hypothesis is that the means of the two populations are the same: µ 1 = µ 2 . The alternative hypothesis is that they are not the same: µ 1 ≠ µ 2 . Again, the test can be one-tailed if the researcher has good reason to expect the difference goes in a particular direction.
The t statistic here is a bit more complicated because it must take into account two sample means, two standard deviations, and two sample sizes. The formula is as follows:
![Rendered by QuickLaTeX.com \[t=\dfrac{M_1-M_2}{\sqrt{\dfrac{{SD_1}^2}{n_1}+\dfrac{{SD_2}^2}{n_2}}}\]](https://opentextbc.ca/researchmethods/wp-content/ql-cache/quicklatex.com-0242d1ab42d68adb3bb852a45bfb9b2d_l3.png)
Notice that this formula includes squared standard deviations (the variances) that appear inside the square root symbol. Also, lowercase n 1 and n 2 refer to the sample sizes in the two groups or condition (as opposed to capital N , which generally refers to the total sample size). The only additional thing to know here is that there are N − 2 degrees of freedom for the independent-samples t test.
Example Independent-Samples t Test
Now the health psychologist wants to compare the calorie estimates of people who regularly eat junk food with the estimates of people who rarely eat junk food. He believes the difference could come out in either direction so he decides to conduct a two-tailed test. He collects data from a sample of eight participants who eat junk food regularly and seven participants who rarely eat junk food. The data are as follows:
Junk food eaters: 180, 220, 150, 85, 200, 170, 150, 190
Non–junk food eaters: 200, 240, 190, 175, 200, 300, 240
The mean for the junk food eaters is 220.71 with a standard deviation of 41.23. The mean for the non–junk food eaters is 168.12 with a standard deviation of 42.66. He can now compute his t score as follows:
![Rendered by QuickLaTeX.com \[t=\dfrac{220.71-168.12}{\sqrt{\dfrac{41.23^2}{8}+\dfrac{42.66^2}{7}}}=2.42\]](https://opentextbc.ca/researchmethods/wp-content/ql-cache/quicklatex.com-8dd797ba37fac6e3618f34946daefb5b_l3.png)
If he enters the data into one of the online analysis tools or uses Excel or SPSS, it would tell him that the two-tailed p value for this t score (with 15 − 2 = 13 degrees of freedom) is .015. Because this p value is less than .05, the health psychologist would reject the null hypothesis and conclude that people who eat junk food regularly make lower calorie estimates than people who eat it rarely. If he were to compute the t score by hand, he could look at Table 13.2 and see that the critical value of t for a two-tailed test with 13 degrees of freedom is ±2.160. The fact that his t score was more extreme than this critical value would tell him that his p value is less than .05 and that he should fail to retain the null hypothesis.
The Analysis of Variance
When there are more than two groups or condition means to be compared, the most common null hypothesis test is the analysis of variance (ANOVA) . In this section, we look primarily at the one-way ANOVA , which is used for between-subjects designs with a single independent variable. We then briefly consider some other versions of the ANOVA that are used for within-subjects and factorial research designs.
One-Way ANOVA
The one-way ANOVA is used to compare the means of more than two samples ( M 1 , M 2 … M G ) in a between-subjects design. The null hypothesis is that all the means are equal in the population: µ 1 = µ 2 =…= µ G . The alternative hypothesis is that not all the means in the population are equal.
The test statistic for the ANOVA is called F . It is a ratio of two estimates of the population variance based on the sample data. One estimate of the population variance is called the mean squares between groups (MS B ) and is based on the differences among the sample means. The other is called the mean squares within groups (MS W ) and is based on the differences among the scores within each group. The F statistic is the ratio of the MS B to the MS W and can therefore be expressed as follows:
F = MS B ÷ MS W
Again, the reason that F is useful is that we know how it is distributed when the null hypothesis is true. As shown in Figure 13.2, this distribution is unimodal and positively skewed with values that cluster around 1. The precise shape of the distribution depends on both the number of groups and the sample size, and there is a degrees of freedom value associated with each of these. The between-groups degrees of freedom is the number of groups minus one: df B = ( G − 1). The within-groups degrees of freedom is the total sample size minus the number of groups: df W = N − G . Again, knowing the distribution of F when the null hypothesis is true allows us to find the p value.
The online tools in Chapter 12 and statistical software such as Excel and SPSS will compute F and find the p value. If p is less than .05, then we reject the null hypothesis and conclude that there are differences among the group means in the population. If p is greater than .05, then we retain the null hypothesis and conclude that there is not enough evidence to say that there are differences. In the unlikely event that we would compute F by hand, we can use a table of critical values like Table 13.3 “Table of Critical Values of ” to make the decision. The idea is that any F ratio greater than the critical value has a p value of less than .05. Thus if the F ratio we compute is beyond the critical value, then we reject the null hypothesis. If the F ratio we compute is less than the critical value, then we retain the null hypothesis.
| 2 | 3 | 4 | |
|---|---|---|---|
| 8 | 4.459 | 4.066 | 3.838 |
| 9 | 4.256 | 3.863 | 3.633 |
| 10 | 4.103 | 3.708 | 3.478 |
| 11 | 3.982 | 3.587 | 3.357 |
| 12 | 3.885 | 3.490 | 3.259 |
| 13 | 3.806 | 3.411 | 3.179 |
| 14 | 3.739 | 3.344 | 3.112 |
| 15 | 3.682 | 3.287 | 3.056 |
| 16 | 3.634 | 3.239 | 3.007 |
| 17 | 3.592 | 3.197 | 2.965 |
| 18 | 3.555 | 3.160 | 2.928 |
| 19 | 3.522 | 3.127 | 2.895 |
| 20 | 3.493 | 3.098 | 2.866 |
| 21 | 3.467 | 3.072 | 2.840 |
| 22 | 3.443 | 3.049 | 2.817 |
| 23 | 3.422 | 3.028 | 2.796 |
| 24 | 3.403 | 3.009 | 2.776 |
| 25 | 3.385 | 2.991 | 2.759 |
| 30 | 3.316 | 2.922 | 2.690 |
| 35 | 3.267 | 2.874 | 2.641 |
| 40 | 3.232 | 2.839 | 2.606 |
| 45 | 3.204 | 2.812 | 2.579 |
| 50 | 3.183 | 2.790 | 2.557 |
| 55 | 3.165 | 2.773 | 2.540 |
| 60 | 3.150 | 2.758 | 2.525 |
| 65 | 3.138 | 2.746 | 2.513 |
| 70 | 3.128 | 2.736 | 2.503 |
| 75 | 3.119 | 2.727 | 2.494 |
| 80 | 3.111 | 2.719 | 2.486 |
| 85 | 3.104 | 2.712 | 2.479 |
| 90 | 3.098 | 2.706 | 2.473 |
| 95 | 3.092 | 2.700 | 2.467 |
| 100 | 3.087 | 2.696 | 2.463 |
Example One-Way ANOVA
Imagine that the health psychologist wants to compare the calorie estimates of psychology majors, nutrition majors, and professional dieticians. He collects the following data:
Psych majors: 200, 180, 220, 160, 150, 200, 190, 200
Nutrition majors: 190, 220, 200, 230, 160, 150, 200, 210, 195
Dieticians: 220, 250, 240, 275, 250, 230, 200, 240
The means are 187.50 ( SD = 23.14), 195.00 ( SD = 27.77), and 238.13 ( SD = 22.35), respectively. So it appears that dieticians made substantially more accurate estimates on average. The researcher would almost certainly enter these data into a program such as Excel or SPSS, which would compute F for him and find the p value. Table 13.4 shows the output of the one-way ANOVA function in Excel for these data. This table is referred to as an ANOVA table. It shows that MS B is 5,971.88, MS W is 602.23, and their ratio, F , is 9.92. The p value is .0009. Because this value is below .05, the researcher would reject the null hypothesis and conclude that the mean calorie estimates for the three groups are not the same in the population. Notice that the ANOVA table also includes the “sum of squares” ( SS ) for between groups and for within groups. These values are computed on the way to finding MS B and MS W but are not typically reported by the researcher. Finally, if the researcher were to compute the F ratio by hand, he could look at Table 13.3 and see that the critical value of F with 2 and 21 degrees of freedom is 3.467 (the same value in Table 13.4 under F crit ). The fact that his F score was more extreme than this critical value would tell him that his p value is less than .05 and that he should reject the null hypothesis.
| Between groups | 11,943.75 | 2 | 5,971.875 | 9.916234 | 0.000928 | 3.4668 |
| Within groups | 12,646.88 | 21 | 602.2321 | |||
| Total | 24,590.63 | 23 |
ANOVA Elaborations
Post hoc comparisons.
When we reject the null hypothesis in a one-way ANOVA, we conclude that the group means are not all the same in the population. But this can indicate different things. With three groups, it can indicate that all three means are significantly different from each other. Or it can indicate that one of the means is significantly different from the other two, but the other two are not significantly different from each other. It could be, for example, that the mean calorie estimates of psychology majors, nutrition majors, and dieticians are all significantly different from each other. Or it could be that the mean for dieticians is significantly different from the means for psychology and nutrition majors, but the means for psychology and nutrition majors are not significantly different from each other. For this reason, statistically significant one-way ANOVA results are typically followed up with a series of post hoc comparisons of selected pairs of group means to determine which are different from which others.
One approach to post hoc comparisons would be to conduct a series of independent-samples t tests comparing each group mean to each of the other group means. But there is a problem with this approach. In general, if we conduct a t test when the null hypothesis is true, we have a 5% chance of mistakenly rejecting the null hypothesis (see Section 13.3 “Additional Considerations” for more on such Type I errors). If we conduct several t tests when the null hypothesis is true, the chance of mistakenly rejecting at least one null hypothesis increases with each test we conduct. Thus researchers do not usually make post hoc comparisons using standard t tests because there is too great a chance that they will mistakenly reject at least one null hypothesis. Instead, they use one of several modified t test procedures—among them the Bonferonni procedure, Fisher’s least significant difference (LSD) test, and Tukey’s honestly significant difference (HSD) test. The details of these approaches are beyond the scope of this book, but it is important to understand their purpose. It is to keep the risk of mistakenly rejecting a true null hypothesis to an acceptable level (close to 5%).
Repeated-Measures ANOVA
Recall that the one-way ANOVA is appropriate for between-subjects designs in which the means being compared come from separate groups of participants. It is not appropriate for within-subjects designs in which the means being compared come from the same participants tested under different conditions or at different times. This requires a slightly different approach, called the repeated-measures ANOVA . The basics of the repeated-measures ANOVA are the same as for the one-way ANOVA. The main difference is that measuring the dependent variable multiple times for each participant allows for a more refined measure of MS W . Imagine, for example, that the dependent variable in a study is a measure of reaction time. Some participants will be faster or slower than others because of stable individual differences in their nervous systems, muscles, and other factors. In a between-subjects design, these stable individual differences would simply add to the variability within the groups and increase the value of MS W . In a within-subjects design, however, these stable individual differences can be measured and subtracted from the value of MS W . This lower value of MS W means a higher value of F and a more sensitive test.
Factorial ANOVA
When more than one independent variable is included in a factorial design, the appropriate approach is the factorial ANOVA . Again, the basics of the factorial ANOVA are the same as for the one-way and repeated-measures ANOVAs. The main difference is that it produces an F ratio and p value for each main effect and for each interaction. Returning to our calorie estimation example, imagine that the health psychologist tests the effect of participant major (psychology vs. nutrition) and food type (cookie vs. hamburger) in a factorial design. A factorial ANOVA would produce separate F ratios and p values for the main effect of major, the main effect of food type, and the interaction between major and food. Appropriate modifications must be made depending on whether the design is between subjects, within subjects, or mixed.
Testing Pearson’s r
For relationships between quantitative variables, where Pearson’s r is used to describe the strength of those relationships, the appropriate null hypothesis test is a test of Pearson’s r . The basic logic is exactly the same as for other null hypothesis tests. In this case, the null hypothesis is that there is no relationship in the population. We can use the Greek lowercase rho (ρ) to represent the relevant parameter: ρ = 0. The alternative hypothesis is that there is a relationship in the population: ρ ≠ 0. As with the t test, this test can be two-tailed if the researcher has no expectation about the direction of the relationship or one-tailed if the researcher expects the relationship to go in a particular direction.
It is possible to use Pearson’s r for the sample to compute a t score with N − 2 degrees of freedom and then to proceed as for a t test. However, because of the way it is computed, Pearson’s r can also be treated as its own test statistic. The online statistical tools and statistical software such as Excel and SPSS generally compute Pearson’s r and provide the p value associated with that value of Pearson’s r . As always, if the p value is less than .05, we reject the null hypothesis and conclude that there is a relationship between the variables in the population. If the p value is greater than .05, we retain the null hypothesis and conclude that there is not enough evidence to say there is a relationship in the population. If we compute Pearson’s r by hand, we can use a table like Table 13.5, which shows the critical values of r for various samples sizes when α is .05. A sample value of Pearson’s r that is more extreme than the critical value is statistically significant.
| Critical value of one-tailed | Critical value of two-tailed | |
|---|---|---|
| 5 | .805 | .878 |
| 10 | .549 | .632 |
| 15 | .441 | .514 |
| 20 | .378 | .444 |
| 25 | .337 | .396 |
| 30 | .306 | .361 |
| 35 | .283 | .334 |
| 40 | .264 | .312 |
| 45 | .248 | .294 |
| 50 | .235 | .279 |
| 55 | .224 | .266 |
| 60 | .214 | .254 |
| 65 | .206 | .244 |
| 70 | .198 | .235 |
| 75 | .191 | .227 |
| 80 | .185 | .220 |
| 85 | .180 | .213 |
| 90 | .174 | .207 |
| 95 | .170 | .202 |
| 100 | .165 | .197 |
Example Test of Pearson’s r
Imagine that the health psychologist is interested in the correlation between people’s calorie estimates and their weight. He has no expectation about the direction of the relationship, so he decides to conduct a two-tailed test. He computes the correlation for a sample of 22 university students and finds that Pearson’s r is −.21. The statistical software he uses tells him that the p value is .348. It is greater than .05, so he retains the null hypothesis and concludes that there is no relationship between people’s calorie estimates and their weight. If he were to compute Pearson’s r by hand, he could look at Table 13.5 and see that the critical value for 22 − 2 = 20 degrees of freedom is .444. The fact that Pearson’s r for the sample is less extreme than this critical value tells him that the p value is greater than .05 and that he should retain the null hypothesis.
Key Takeaways
- To compare two means, the most common null hypothesis test is the t test. The one-sample t test is used for comparing one sample mean with a hypothetical population mean of interest, the dependent-samples t test is used to compare two means in a within-subjects design, and the independent-samples t test is used to compare two means in a between-subjects design.
- To compare more than two means, the most common null hypothesis test is the analysis of variance (ANOVA). The one-way ANOVA is used for between-subjects designs with one independent variable, the repeated-measures ANOVA is used for within-subjects designs, and the factorial ANOVA is used for factorial designs.
- A null hypothesis test of Pearson’s r is used to compare a sample value of Pearson’s r with a hypothetical population value of 0.
- Practice: Use one of the online tools, Excel, or SPSS to reproduce the one-sample t test, dependent-samples t test, independent-samples t test, and one-way ANOVA for the four sets of calorie estimation data presented in this section.
- Practice: A sample of 25 university students rated their friendliness on a scale of 1 ( Much Lower Than Average ) to 7 ( Much Higher Than Average ). Their mean rating was 5.30 with a standard deviation of 1.50. Conduct a one-sample t test comparing their mean rating with a hypothetical mean rating of 4 ( Average ). The question is whether university students have a tendency to rate themselves as friendlier than average.
- The correlation between height and IQ is +.13 in a sample of 35.
- For a sample of 88 university students, the correlation between how disgusted they felt and the harshness of their moral judgments was +.23.
- The correlation between the number of daily hassles and positive mood is −.43 for a sample of 30 middle-aged adults.
A common null hypothesis test examining the difference between two means.
Compares a sample mean with a hypothetical population mean that provides some interesting standard of comparison.
A statistic that is computed only to help find the p value.
Points on the test distribution that are compared to the test statistic to determine whether to reject the null hypothesis.
The null hypothesis is rejected if the t score for the sample is extreme in either direction.
Where the null hypothesis is rejected only if the t score for the sample is extreme in one direction that we specify before collecting the data.
Statistical test used to compare two means for the same sample tested at two different times or under two different conditions.
Variable formed by subtracting one variable from another.
Statistical test used to compare the means of two separate samples.
Most common null hypothesis test when there are more than two groups or condition means to be compared.
A null hypothesis test that is used for between-between subjects designs with a single independent variable.
An estimate of population variance based on the differences among the sample means.
An estimate of population variance based on the differences among the scores within each group.
Analysis of selected pairs of group means to determine which are different from which others.
The dependent variable is measured multiple times for each participant, allowing a more refined measure of MSW.
A null hypothesis test that is used when more than one independent variable is included in a factorial design.
Research Methods in Psychology - 2nd Canadian Edition Copyright © 2015 by Paul C. Price, Rajiv Jhangiani, & I-Chant A. Chiang is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
13.1 Understanding Null Hypothesis Testing
Learning objectives.
- Explain the purpose of null hypothesis testing, including the role of sampling error.
- Describe the basic logic of null hypothesis testing.
- Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.
The Purpose of Null Hypothesis Testing
As we have seen, psychological research typically involves measuring one or more variables in a sample and computing descriptive statistics for that sample. In general, however, the researcher’s goal is not to draw conclusions about that sample but to draw conclusions about the population that the sample was selected from. Thus researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called parameters . Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 adults with clinical depression and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for adults with clinical depression).
Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of adults with clinical depression, 6.45 in a second sample, and 9.44 in a third—even though these samples are selected randomly from the same population. Similarly, the correlation (Pearson’s r ) between two variables might be +.24 in one sample, −.04 in a second sample, and +.15 in a third—again, even though these samples are selected randomly from the same population. This random variability in a statistic from sample to sample is called sampling error . (Note that the term error here refers to random variability and does not imply that anyone has made a mistake. No one “commits a sampling error.”)
One implication of this is that when there is a statistical relationship in a sample, it is not always clear that there is a statistical relationship in the population. A small difference between two group means in a sample might indicate that there is a small difference between the two group means in the population. But it could also be that there is no difference between the means in the population and that the difference in the sample is just a matter of sampling error. Similarly, a Pearson’s r value of −.29 in a sample might mean that there is a negative relationship in the population. But it could also be that there is no relationship in the population and that the relationship in the sample is just a matter of sampling error.
In fact, any statistical relationship in a sample can be interpreted in two ways:
- There is a relationship in the population, and the relationship in the sample reflects this.
- There is no relationship in the population, and the relationship in the sample reflects only sampling error.
The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.
The Logic of Null Hypothesis Testing
Null hypothesis testing is a formal approach to deciding between two interpretations of a statistical relationship in a sample. One interpretation is called the null hypothesis (often symbolized H 0 and read as “H-naught”). This is the idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error. Informally, the null hypothesis is that the sample relationship “occurred by chance.” The other interpretation is called the alternative hypothesis (often symbolized as H 1 ). This is the idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.
Again, every statistical relationship in a sample can be interpreted in either of these two ways: It might have occurred by chance, or it might reflect a relationship in the population. So researchers need a way to decide between them. Although there are many specific null hypothesis testing techniques, they are all based on the same general logic. The steps are as follows:
- Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
- Determine how likely the sample relationship would be if the null hypothesis were true.
- If the sample relationship would be extremely unlikely, then reject the null hypothesis in favor of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis .
Following this logic, we can begin to understand why Mehl and his colleagues concluded that there is no difference in talkativeness between women and men in the population. In essence, they asked the following question: “If there were no difference in the population, how likely is it that we would find a small difference of d = 0.06 in our sample?” Their answer to this question was that this sample relationship would be fairly likely if the null hypothesis were true. Therefore, they retained the null hypothesis—concluding that there is no evidence of a sex difference in the population. We can also see why Kanner and his colleagues concluded that there is a correlation between hassles and symptoms in the population. They asked, “If the null hypothesis were true, how likely is it that we would find a strong correlation of +.60 in our sample?” Their answer to this question was that this sample relationship would be fairly unlikely if the null hypothesis were true. Therefore, they rejected the null hypothesis in favor of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population.
A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value . A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A p value that is not low means that the sample result would be likely if the null hypothesis were true and leads to the retention of the null hypothesis. But how low must the p value be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is a 5% chance or less of a result as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant . If there is greater than a 5% chance of a result as extreme as the sample result when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to reject it. Researchers often use the expression “fail to reject the null hypothesis” rather than “retain the null hypothesis,” but they never use the expression “accept the null hypothesis.”
The Misunderstood p Value
The p value is one of the most misunderstood quantities in psychological research (Cohen, 1994) [1] . Even professional researchers misinterpret it, and it is not unusual for such misinterpretations to appear in statistics textbooks!
The most common misinterpretation is that the p value is the probability that the null hypothesis is true—that the sample result occurred by chance. For example, a misguided researcher might say that because the p value is .02, there is only a 2% chance that the result is due to chance and a 98% chance that it reflects a real relationship in the population. But this is incorrect . The p value is really the probability of a result at least as extreme as the sample result if the null hypothesis were true. So a p value of .02 means that if the null hypothesis were true, a sample result this extreme would occur only 2% of the time.
You can avoid this misunderstanding by remembering that the p value is not the probability that any particular hypothesis is true or false. Instead, it is the probability of obtaining the sample result if the null hypothesis were true.

“Null Hypothesis” retrieved from http://imgs.xkcd.com/comics/null_hypothesis.png (CC-BY-NC 2.5)
Role of Sample Size and Relationship Strength
Recall that null hypothesis testing involves answering the question, “If the null hypothesis were true, what is the probability of a sample result as extreme as this one?” In other words, “What is the p value?” It can be helpful to see that the answer to this question depends on just two considerations: the strength of the relationship and the size of the sample. Specifically, the stronger the sample relationship and the larger the sample, the less likely the result would be if the null hypothesis were true. That is, the lower the p value. This should make sense. Imagine a study in which a sample of 500 women is compared with a sample of 500 men in terms of some psychological characteristic, and Cohen’s d is a strong 0.50. If there were really no sex difference in the population, then a result this strong based on such a large sample should seem highly unlikely. Now imagine a similar study in which a sample of three women is compared with a sample of three men, and Cohen’s d is a weak 0.10. If there were no sex difference in the population, then a relationship this weak based on such a small sample should seem likely. And this is precisely why the null hypothesis would be rejected in the first example and retained in the second.
Of course, sometimes the result can be weak and the sample large, or the result can be strong and the sample small. In these cases, the two considerations trade off against each other so that a weak result can be statistically significant if the sample is large enough and a strong relationship can be statistically significant even if the sample is small. Table 13.1 shows roughly how relationship strength and sample size combine to determine whether a sample result is statistically significant. The columns of the table represent the three levels of relationship strength: weak, medium, and strong. The rows represent four sample sizes that can be considered small, medium, large, and extra large in the context of psychological research. Thus each cell in the table represents a combination of relationship strength and sample size. If a cell contains the word Yes , then this combination would be statistically significant for both Cohen’s d and Pearson’s r . If it contains the word No , then it would not be statistically significant for either. There is one cell where the decision for d and r would be different and another where it might be different depending on some additional considerations, which are discussed in Section 13.2 “Some Basic Null Hypothesis Tests”
| Sample Size | Weak | Medium | Strong |
| Small ( = 20) | No | No | = Maybe = Yes |
| Medium ( = 50) | No | Yes | Yes |
| Large ( = 100) | = Yes = No | Yes | Yes |
| Extra large ( = 500) | Yes | Yes | Yes |
Although Table 13.1 provides only a rough guideline, it shows very clearly that weak relationships based on medium or small samples are never statistically significant and that strong relationships based on medium or larger samples are always statistically significant. If you keep this lesson in mind, you will often know whether a result is statistically significant based on the descriptive statistics alone. It is extremely useful to be able to develop this kind of intuitive judgment. One reason is that it allows you to develop expectations about how your formal null hypothesis tests are going to come out, which in turn allows you to detect problems in your analyses. For example, if your sample relationship is strong and your sample is medium, then you would expect to reject the null hypothesis. If for some reason your formal null hypothesis test indicates otherwise, then you need to double-check your computations and interpretations. A second reason is that the ability to make this kind of intuitive judgment is an indication that you understand the basic logic of this approach in addition to being able to do the computations.
Statistical Significance Versus Practical Significance
Table 13.1 illustrates another extremely important point. A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is closely related to Janet Shibley Hyde’s argument about sex differences (Hyde, 2007) [2] . The differences between women and men in mathematical problem solving and leadership ability are statistically significant. But the word significant can cause people to interpret these differences as strong and important—perhaps even important enough to influence the college courses they take or even who they vote for. As we have seen, however, these statistically significant differences are actually quite weak—perhaps even “trivial.”
This is why it is important to distinguish between the statistical significance of a result and the practical significance of that result. Practical significance refers to the importance or usefulness of the result in some real-world context. Many sex differences are statistically significant—and may even be interesting for purely scientific reasons—but they are not practically significant. In clinical practice, this same concept is often referred to as “clinical significance.” For example, a study on a new treatment for social phobia might show that it produces a statistically significant positive effect. Yet this effect still might not be strong enough to justify the time, effort, and other costs of putting it into practice—especially if easier and cheaper treatments that work almost as well already exist. Although statistically significant, this result would be said to lack practical or clinical significance.

“Conditional Risk” retrieved from http://imgs.xkcd.com/comics/conditional_risk.png (CC-BY-NC 2.5)
Key Takeaways
- Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance.
- The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favor of the alternative hypothesis. If it would not be unlikely, then the null hypothesis is retained.
- The probability of obtaining the sample result if the null hypothesis were true (the p value) is based on two considerations: relationship strength and sample size. Reasonable judgments about whether a sample relationship is statistically significant can often be made by quickly considering these two factors.
- Statistical significance is not the same as relationship strength or importance. Even weak relationships can be statistically significant if the sample size is large enough. It is important to consider relationship strength and the practical significance of a result in addition to its statistical significance.
- Discussion: Imagine a study showing that people who eat more broccoli tend to be happier. Explain for someone who knows nothing about statistics why the researchers would conduct a null hypothesis test.
- The correlation between two variables is r = −.78 based on a sample size of 137.
- The mean score on a psychological characteristic for women is 25 ( SD = 5) and the mean score for men is 24 ( SD = 5). There were 12 women and 10 men in this study.
- In a memory experiment, the mean number of items recalled by the 40 participants in Condition A was 0.50 standard deviations greater than the mean number recalled by the 40 participants in Condition B.
- In another memory experiment, the mean scores for participants in Condition A and Condition B came out exactly the same!
- A student finds a correlation of r = .04 between the number of units the students in his research methods class are taking and the students’ level of stress.
- Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003. ↵
- Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science, 16 , 259–263. ↵

Share This Book
- Increase Font Size
- Search Search Please fill out this field.
What Is a Null Hypothesis?
The alternative hypothesis.
- Additional Examples
- Null Hypothesis and Investments
The Bottom Line
- Corporate Finance
- Financial Ratios
Null Hypothesis: What Is It, and How Is It Used in Investing?
Adam Hayes, Ph.D., CFA, is a financial writer with 15+ years Wall Street experience as a derivatives trader. Besides his extensive derivative trading expertise, Adam is an expert in economics and behavioral finance. Adam received his master's in economics from The New School for Social Research and his Ph.D. from the University of Wisconsin-Madison in sociology. He is a CFA charterholder as well as holding FINRA Series 7, 55 & 63 licenses. He currently researches and teaches economic sociology and the social studies of finance at the Hebrew University in Jerusalem.
:max_bytes(150000):strip_icc():format(webp)/adam_hayes-5bfc262a46e0fb005118b414.jpg)
A null hypothesis is a type of statistical hypothesis that proposes that no statistical significance exists in a set of given observations. Hypothesis testing is used to assess the credibility of a hypothesis by using sample data. Sometimes referred to simply as the “null,” it is represented as H 0 .
The null hypothesis, also known as “the conjecture,” is used in quantitative analysis to test theories about markets, investing strategies, and economies to decide if an idea is true or false.
Key Takeaways
- A null hypothesis is a type of conjecture in statistics that proposes that there is no difference between certain characteristics of a population or data-generating process.
- The alternative hypothesis proposes that there is a difference.
- Hypothesis testing provides a method to reject a null hypothesis within a certain confidence level.
- If you can reject the null hypothesis, it provides support for the alternative hypothesis.
- Null hypothesis testing is the basis of the principle of falsification in science.
Alex Dos Diaz / Investopedia
Understanding a Null Hypothesis
A gambler may be interested in whether a game of chance is fair. If it is, then the expected earnings per play come to zero for both players. If it is not, then the expected earnings are positive for one player and negative for the other.
To test whether the game is fair, the gambler collects earnings data from many repetitions of the game, calculates the average earnings from these data, then tests the null hypothesis that the expected earnings are not different from zero.
If the average earnings from the sample data are sufficiently far from zero, then the gambler will reject the null hypothesis and conclude the alternative hypothesis—namely, that the expected earnings per play are different from zero. If the average earnings from the sample data are near zero, then the gambler will not reject the null hypothesis, concluding instead that the difference between the average from the data and zero is explainable by chance alone.
A null hypothesis can only be rejected, not proven.
The null hypothesis assumes that any kind of difference between the chosen characteristics that you see in a set of data is due to chance. For example, if the expected earnings for the gambling game are truly equal to zero, then any difference between the average earnings in the data and zero is due to chance.
Analysts look to reject the null hypothesis because doing so is a strong conclusion. This requires evidence in the form of an observed difference that is too large to be explained solely by chance. Failing to reject the null hypothesis—that the results are explainable by chance alone—is a weak conclusion because it allows that while factors other than chance may be at work, they may not be strong enough for the statistical test to detect them.
An important point to note is that we are testing the null hypothesis because there is an element of doubt about its validity. Whatever information that is against the stated null hypothesis is captured in the alternative (alternate) hypothesis (H 1 ).
For the examples below, the alternative hypothesis would be:
- Students score an average that is not equal to seven.
- The mean annual return of a mutual fund is not equal to 8% per year.
In other words, the alternative hypothesis is a direct contradiction of the null hypothesis.
Null Hypothesis Examples
Here is a simple example: A school principal claims that students in her school score an average of seven out of 10 in exams. The null hypothesis is that the population mean is not 7.0. To test this null hypothesis, we record marks of, say, 30 students ( sample ) from the entire student population of the school (say, 300) and calculate the mean of that sample.
We can then compare the (calculated) sample mean to the (hypothesized) population mean of 7.0 and attempt to reject the null hypothesis. (The null hypothesis here—that the population mean is not 7.0—cannot be proved using the sample data. It can only be rejected.)
Take another example: The annual return of a particular mutual fund is claimed to be 8%. Assume that the mutual fund has been in existence for 20 years. The null hypothesis is that the mean return is not 8% for the mutual fund. We take a random sample of annual returns of the mutual fund for, say, five years (sample) and calculate the sample mean. We then compare the (calculated) sample mean to the (claimed) population mean (8%) to test the null hypothesis.
For the above examples, null hypotheses are:
- Example A: Students in the school don’t score an average of seven out of 10 in exams.
- Example B: The mean annual return of the mutual fund is not 8% per year.
For the purposes of determining whether to reject the null hypothesis (abbreviated H0), said hypothesis is assumed, for the sake of argument, to be true. Then the likely range of possible values of the calculated statistic (e.g., the average score on 30 students’ tests) is determined under this presumption (e.g., the range of plausible averages might range from 6.2 to 7.8 if the population mean is 7.0).
If the sample average is outside of this range, the null hypothesis is rejected. Otherwise, the difference is said to be “explainable by chance alone,” being within the range that is determined by chance alone.
How Null Hypothesis Testing Is Used in Investments
As an example related to financial markets, assume Alice sees that her investment strategy produces higher average returns than simply buying and holding a stock . The null hypothesis states that there is no difference between the two average returns, and Alice is inclined to believe this until she can conclude contradictory results.
Refuting the null hypothesis would require showing statistical significance, which can be found by a variety of tests. The alternative hypothesis would state that the investment strategy has a higher average return than a traditional buy-and-hold strategy.
One tool that can determine the statistical significance of the results is the p-value. A p-value represents the probability that a difference as large or larger than the observed difference between the two average returns could occur solely by chance.
A p-value that is less than or equal to 0.05 often indicates whether there is evidence against the null hypothesis. If Alice conducts one of these tests, such as a test using the normal model, resulting in a significant difference between her returns and the buy-and-hold returns (the p-value is less than or equal to 0.05), she can then reject the null hypothesis and conclude the alternative hypothesis.
How Is the Null Hypothesis Identified?
The analyst or researcher establishes a null hypothesis based on the research question or problem they are trying to answer. Depending on the question, the null may be identified differently. For example, if the question is simply whether an effect exists (e.g., does X influence Y?), the null hypothesis could be H 0 : X = 0. If the question is instead, is X the same as Y, the H 0 would be X = Y. If it is that the effect of X on Y is positive, H 0 would be X > 0. If the resulting analysis shows an effect that is statistically significantly different from zero, the null can be rejected.
How Is Null Hypothesis Used in Finance?
In finance , a null hypothesis is used in quantitative analysis. It tests the premise of an investing strategy, the markets, or an economy to determine if it is true or false.
For instance, an analyst may want to see if two stocks, ABC and XYZ, are closely correlated. The null hypothesis would be ABC ≠ XYZ.
How Are Statistical Hypotheses Tested?
Statistical hypotheses are tested by a four-step process . The first is for the analyst to state the two hypotheses so that only one can be right. The second is to formulate an analysis plan, which outlines how the data will be evaluated. The third is to carry out the plan and physically analyze the sample data. The fourth and final step is to analyze the results and either reject the null hypothesis or claim that the observed differences are explainable by chance alone.
What Is an Alternative Hypothesis?
An alternative hypothesis is a direct contradiction of a null hypothesis. This means that if one of the two hypotheses is true, the other is false.
A null hypothesis states there is no difference between groups or relationship between variables. It is a type of statistical hypothesis and proposes that no statistical significance exists in a set of given observations. “Null” means nothing.
The null hypothesis is used in quantitative analysis to test theories about economies, investing strategies, and markets to decide if an idea is true or false. Hypothesis testing assesses the credibility of a hypothesis by using sample data. It is represented as H 0 and is sometimes simply known as “the null.”
Sage Publishing. “ Chapter 8: Introduction to Hypothesis Testing ,” Page 4.
Sage Publishing. “ Chapter 8: Introduction to Hypothesis Testing ,” Pages 4 to 7.
Sage Publishing. “ Chapter 8: Introduction to Hypothesis Testing ,” Page 7.
:max_bytes(150000):strip_icc():format(webp)/businessperson-calculating-invoice-949219374-5258a9aa6bcd48c5b7af835a15a3935c.jpg)
- Terms of Service
- Editorial Policy
- Privacy Policy
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Why do statisticians say a non-significant result means "you can't reject the null" as opposed to accepting the null hypothesis?
Traditional statistical tests, like the two sample t-test, focus on trying to eliminate the hypothesis that there is no difference between a function of two independent samples. Then, we choose a confidence level and say that if the difference of means is beyond the 95% level, we can reject the null hypothesis. If not, we "can't reject the null hypothesis". This seems to imply that we can't accept it either. Does it mean we're not sure if the null hypothesis is true?
Now, I want to design a test where my hypothesis is that a function of two samples is the same (which is the opposite of traditional statistics tests where the hypothesis is that the two samples are different). So, my null hypothesis becomes that the two samples are different. How should I design such a test? Will it be as simple as saying that if the p-value is lesser than 5% we can accept the hypothesis that there is no significant difference?
- hypothesis-testing
- statistical-significance
- confidence-interval
- equivalence
- 1 $\begingroup$ Very related: Does failure to reject the null in Neyman-Pearson approach mean that one should “accept” it? $\endgroup$ – amoeba Commented Dec 9, 2016 at 23:25
- $\begingroup$ difference of means is beyond the 95% level, we can reject the null hypothesis. The 95% is not a "level" it is here in 95 cases out of 100 cases (comparisons), the differennce in sample-statistic arises due to sampling fluctuations. it means that null is accepted at alpha = .05. Saying 95% level is not correct term. $\endgroup$ – user10619 Commented Apr 23, 2019 at 6:07
4 Answers 4
Traditionally, the null hypothesis is a point value. (It is typically $0$, but can in fact be any point value.) The alternative hypothesis is that the true value is any value other than the null value . Because a continuous variable (such as a mean difference) can take on a value which is indefinitely close to the null value but still not quite equal and thus make the null hypothesis false, a traditional point null hypothesis cannot be proven.
Imagine your null hypothesis is $0$, and the mean difference you observe is $0.01$. Is it reasonable to assume the null hypothesis is true? You don't know yet; it would be helpful to know what our confidence interval looks like. Let's say that your 95% confidence interval is $(-4.99,\ 5.01)$. Now, should we conclude that the true value is $0$? I would not feel comfortable saying that, because the CI is very wide, and there are many, large non-zero values that we might reasonably suspect are consistent with our data. So let's say we gather much, much more data, and now our observed mean difference is $0.01$, but the 95% CI is $(0.005,\ 0.015)$. The observed mean difference has stayed the same (which would be amazing if it really happened), but the confidence interval now excludes the null value. Of course, this is just a thought experiment, but it should make the basic ideas clear. We can never prove that the true value is any particular point value; we can only (possibly) disprove that it is some point value. In statistical hypothesis testing, the fact that the p-value is > 0.05 (and that the 95% CI includes zero) means that we are not sure if the null hypothesis is true .
As for your concrete case, you cannot construct a test where the alternative hypothesis is that the mean difference is $0$ and the null hypothesis is anything other than zero. This violates the logic of hypothesis testing. It is perfectly reasonable that it is your substantive, scientific hypothesis, but it cannot be your alternative hypothesis in a hypothesis testing situation.
So what can you do? In this situation, you use equivalence testing. (You might want to read through some of our threads on this topic by clicking on the equivalence tag.) The typical strategy is to use the two one sided tests approach. Very briefly, you select an interval within which you would consider that the true mean difference might as well be $0$ for all you could care, then you perform a one-sided test to determine if the observed value is less than the upper bound of that interval, and another one-sided test to see if it is greater than the lower bound. If both of these tests are significant, then you have rejected the hypothesis that the true value is outside the interval you care about. If one (or both) are non-significant, you fail to reject the hypothesis that the true value is outside the interval.
For example, suppose anything within the interval $(-0.02,\ 0.02)$ is so close to zero that you think it is essentially the same as zero for your purposes, so you use that as your substantive hypothesis. Now imagine that you get the first result described above. Although $0.01$ falls within that interval, you would not be able to reject the null hypothesis on either one-sided t-test, so you would fail to reject the null hypothesis. On the other hand, imagine that you got the second result described above. Now you find that the observed value falls within the designated interval, and it can be shown to be both less than the upper bound and greater than the lower bound, so you can reject the null. (It is worth noting that you can reject both the hypothesis that the true value is $0$, and the hypothesis that the true value lies outside of the interval $(-0.02,\ 0.02)$, which may seem perplexing at first, but is fully consistent with the logic of hypothesis testing.)
- 2 $\begingroup$ "Traditionally, the null hypothesis is a point value" - though in some cases we write the null hypothesis as if it were point, yet actually it's compound . I'm curious what implication the argument in your first paragraph therefore has for one-sided tests. (Since we don't - as far as I know - write "accept $H_0$" even for one-sided tests, I'm not sure the first paragraph captures the true reason we don't write "accept $H_0$.) $\endgroup$ – Silverfish Commented Jan 5, 2015 at 14:19
- 1 $\begingroup$ @Silverfish, the paragraph ends with: "a traditional point null hypothesis cannot be proven". However, we also don't write "accept $H_0$" for one-sided tests for the same reason. When $H_0: \delta\le 0$, the true $\delta$ can be $>0$, but arbitrarily close & thus non-significant. If you really wanted to show that it was $<0$, then you can flip the direction of the one-sided test. I don't see a problem here. $\endgroup$ – gung - Reinstate Monica Commented Jan 5, 2015 at 14:26
- 1 $\begingroup$ I'm not saying what you wrote is wrong and I suspected that was the idea you were trying to communicate. Obviously the reason you have tackled the two-sided test with a point hypothesis in the first two paragraphs of your answer, is that this the case in the question. But if your answer is re-read by someone wondering about why we don't "accept $H_0$" in general, it may not be clear to them that your argument actually extends beyond point null hypotheses. $\endgroup$ – Silverfish Commented Jan 5, 2015 at 14:45
- 5 $\begingroup$ The argument "we can never prove that the true value is any particular point value; we can only (possibly) disprove that it is some point value" is a particular case in point - what if the CI had turned out to be (-0.015, -0.005)? To whatever extent we have "proved" $\delta \neq 0$ (I know you don't use "prove" in the literal, mathematical sense - perhaps "demonstrate" or "suggest" are closer to the intended meaning) it seems we have also "proved" $\delta \leq 0$, yet still we would not "accept" $H_0:\,\delta \leq 0$ $\endgroup$ – Silverfish Commented Jan 5, 2015 at 14:48
- 1 $\begingroup$ @Silverfish I think your last comment makes a good point. I feel that, philosophically, one-sided testing with $H_0:\delta<0$ is quite a bit different from two-sided with point null $H_0:\delta=0$, even though mathematically they are almost the same. Accepting point null does not make sense; but testing $\delta>0$ against $\delta<0$ can actually lead to accepting one of them (or an inconclusive result). Plus one-sided testing makes more sense from Bayesian perspective. Plus scientific prediction should have a direction. I guess I start thinking that one-sided testing is not appreciated enough. $\endgroup$ – amoeba Commented Dec 5, 2016 at 22:20
Consider the case where the null hypothesis is that a coin is 2 headed, i.e. the probability of heads is 1. Now the data is the result of flipping a coin a single time and seeing heads. This results in a p-value of 1.0 which is greater than every reasonable alpha. Does this mean that the coin is 2 headed? it could be, but it could also be a fair coin and we saw heads due to chance (would happen 50% of the time with a fair coin). So the high p-value in this case says that the observed data is perfectly consistent with the null, but it is also consistent with other possibilities.
Just like a "Not Guilty" verdict in court can mean the defendant is innocent, it can also be because the defendant is guilty but there is not enough evidence. The same with the null hypothesis we fail to reject because the null could be true, or it could be we don't have enough evidence to reject even though it is false.
- 5 $\begingroup$ I like the "Not guilty" example. Going one step further, re-opening cases based on DNA evidence that we did not know how to use in the past and having some convictions overturned is a perfect example of how adding more data may be all that's needed to have enough evidence. $\endgroup$ – Thomas Speidel Commented Feb 10, 2014 at 15:21
Absence of evidence is not evidence of an absence (the title of an Altman, Bland paper on BMJ). P-values only give us evidence of an absence when we consider them significant. Otherwise, they tell us nothing. Hence, absence of evidence. In other words: we don't know and more data may help.
- 11 $\begingroup$ sigh...yet again I see this quote being stated and yet again i must point out it is a false statement. absence of evidence is not proof of absence. It is evidence of absence though. Think - if I ingest a new substance it might be poisoness. After doing this once and finding no side effects - I have got evidence of absence of poison, from the absence of an effect in the data I observed. But it's not proof (maybe I was lucky), for this would require more data, as you say. $\endgroup$ – probabilityislogic Commented Jul 16, 2020 at 12:12
- $\begingroup$ A properly powered hypothesis test that fails to reject the null is absolutely evidence of absence. Sufficient power means that you likely would have rejected the null if it were indeed false, the fact that you didn't implies that it is not false. This answer suggests that if you check to see if there's an elephant in your closet and don't see one, it is not evidence that your closet is elephant-free. $\endgroup$ – Nuclear Hoagie Commented Nov 7, 2022 at 13:44
The null hypothesis, $H_0$, is usually taken to be the thing you have reason to assume. Often times it is the "current state of knowledge" that you wish to show is statistically unlikely.
The usual set-up for hypothesis testing is minimize type I error , that is, minimize the chance that we reject the null hypothesis in favor of the alternative $H_1$ even though $H_0$ is true. This is the error we choose to first minimize because we don't want to overturn common knowledge when that common knowledge is indeed true.
You should always design your test bearing in mind that $H_0$ should be what you expect.
If we have two samples we expect to be identically distributed then our null hypothesis is the samples are the same. If we have two samples that we would expect to be (wildly) different, our null hypothesis is that they are different.
- $\begingroup$ And what if we have no expectations.. it might be that we just don't know. Also, how will the decision rule work if we want to reject the hypothesis that the two samples are different? $\endgroup$ – ryu576 Commented Feb 8, 2014 at 21:12
- $\begingroup$ In the case you have no expectations you want to keep both both types of errors small but this isn't always possible. You need an extra variable (such as increasing sample size) to do it. $\endgroup$ – SomeEE Commented Feb 8, 2014 at 21:31
- 3 $\begingroup$ Since we can reject the null but not prove it true the null is usually the opposite of what we want to prove or assume to be true. If we believe that there is a difference then the null should be no difference so that you can disprove that. $\endgroup$ – Greg Snow Commented Feb 8, 2014 at 22:03
- $\begingroup$ @Greg That is a good approach if you know which one you want to be true which is probably the usual case. $\endgroup$ – SomeEE Commented Feb 8, 2014 at 22:08
- 2 $\begingroup$ "What you expect" and "that they are different" cannot be statistical hypotheses at all because they are not quantitative. That gets to the crux of the matter: the asymmetry in roles between the null and alternative hypotheses derives from the ability to determine the sampling distribution of the test statistic under the null, compared to the need to parameterize the distribution by the effect size under the alternative hypothesis. Nor is it the case the we "minimize Type I error": that never happens (the minimum is always 0). Tests seek a balance between Type I and II error rates. $\endgroup$ – whuber ♦ Commented Feb 10, 2014 at 15:31
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged hypothesis-testing statistical-significance confidence-interval equivalence tost or ask your own question .
- Featured on Meta
- Announcing a change to the data-dump process
- Bringing clarity to status tag usage on meta sites
Hot Network Questions
- Can I Use A Server In International Waters To Provide Illegal Content Without Getting Arrested?
- Is there an error in Lurie, HTT, Proposition 6.1.2.6.?
- Long and protected macros in LaTeX3
- How to run only selected lines of a shell script?
- What's the difference? lie down vs lie
- Work required to bring a charge from an infinite distance away to the midpoint of a dipole
- Escape from the magic prison
- Is response variable/dependent variable data required for simr simulation?
- Is there a way to do a PhD such that you get a broad view of a field or subfield as a whole?
- Find the global maxima over the interval [0,1]
- Numbering Equations in a Closed Bracket
- In macro "@k", using ^M at end of "call function()" executes the function, but also undesirably adds a new line to my text
- Getting error with passthroughservice while upgrading from sitecore 9 to 10.2
- Risks of exposing professional email accounts?
- Directory of Vegan Communities in Ecuador (South America)
- Invest smaller lump sum vs investing (larger) monthly amount
- Does the average income in the US drop by $9,500 if you exclude the ten richest Americans?
- What's "the archetypal book" called?
- You find yourself locked in a room
- Is the front wheel supposed to turn 360 degrees?
- Referencing an other tikzpicture without overlay
- If a Palestinian converts to Judaism, can they get Israeli citizenship?
- Can Christian Saudi Nationals visit Mecca?
- Microsoft SQL In-Memory OLTP in SQL Express 2019/2022

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
13.1 Understanding Null Hypothesis Testing
Learning objectives.
- Explain the purpose of null hypothesis testing, including the role of sampling error.
- Describe the basic logic of null hypothesis testing.
- Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.
The Purpose of Null Hypothesis Testing
As we have seen, psychological research typically involves measuring one or more variables for a sample and computing descriptive statistics for that sample. In general, however, the researcher’s goal is not to draw conclusions about that sample but to draw conclusions about the population that the sample was selected from. Thus researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called parameters . Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 clinically depressed adults and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for clinically depressed adults).
Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of clinically depressed adults, 6.45 in a second sample, and 9.44 in a third—even though these samples are selected randomly from the same population. Similarly, the correlation (Pearson’s r ) between two variables might be +.24 in one sample, −.04 in a second sample, and +.15 in a third—again, even though these samples are selected randomly from the same population. This random variability in a statistic from sample to sample is called sampling error . (Note that the term error here refers to random variability and does not imply that anyone has made a mistake. No one “commits a sampling error.”)
One implication of this is that when there is a statistical relationship in a sample, it is not always clear that there is a statistical relationship in the population. A small difference between two group means in a sample might indicate that there is a small difference between the two group means in the population. But it could also be that there is no difference between the means in the population and that the difference in the sample is just a matter of sampling error. Similarly, a Pearson’s r value of −.29 in a sample might mean that there is a negative relationship in the population. But it could also be that there is no relationship in the population and that the relationship in the sample is just a matter of sampling error.
In fact, any statistical relationship in a sample can be interpreted in two ways:
- There is a relationship in the population, and the relationship in the sample reflects this.
- There is no relationship in the population, and the relationship in the sample reflects only sampling error.
The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.
The Logic of Null Hypothesis Testing
Null hypothesis testing is a formal approach to deciding between two interpretations of a statistical relationship in a sample. One interpretation is called the null hypothesis (often symbolized H 0 and read as “H-naught”). This is the idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error. Informally, the null hypothesis is that the sample relationship “occurred by chance.” The other interpretation is called the alternative hypothesis (often symbolized as H 1 ). This is the idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.
Again, every statistical relationship in a sample can be interpreted in either of these two ways: It might have occurred by chance, or it might reflect a relationship in the population. So researchers need a way to decide between them. Although there are many specific null hypothesis testing techniques, they are all based on the same general logic. The steps are as follows:
- Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
- Determine how likely the sample relationship would be if the null hypothesis were true.
- If the sample relationship would be extremely unlikely, then reject the null hypothesis in favor of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis .
Following this logic, we can begin to understand why Mehl and his colleagues concluded that there is no difference in talkativeness between women and men in the population. In essence, they asked the following question: “If there were no difference in the population, how likely is it that we would find a small difference of d = 0.06 in our sample?” Their answer to this question was that this sample relationship would be fairly likely if the null hypothesis were true. Therefore, they retained the null hypothesis—concluding that there is no evidence of a sex difference in the population. We can also see why Kanner and his colleagues concluded that there is a correlation between hassles and symptoms in the population. They asked, “If the null hypothesis were true, how likely is it that we would find a strong correlation of +.60 in our sample?” Their answer to this question was that this sample relationship would be fairly unlikely if the null hypothesis were true. Therefore, they rejected the null hypothesis in favor of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population.
A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value . A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A high p value means that the sample result would be likely if the null hypothesis were true and leads to the retention of the null hypothesis. But how low must the p value be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is less than a 5% chance of a result as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant . If there is greater than a 5% chance of a result as extreme as the sample result when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to conclude that it is true. Researchers often use the expression “fail to reject the null hypothesis” rather than “retain the null hypothesis,” but they never use the expression “accept the null hypothesis.”
The Misunderstood p Value
The p value is one of the most misunderstood quantities in psychological research (Cohen, 1994). Even professional researchers misinterpret it, and it is not unusual for such misinterpretations to appear in statistics textbooks!
The most common misinterpretation is that the p value is the probability that the null hypothesis is true—that the sample result occurred by chance. For example, a misguided researcher might say that because the p value is .02, there is only a 2% chance that the result is due to chance and a 98% chance that it reflects a real relationship in the population. But this is incorrect . The p value is really the probability of a result at least as extreme as the sample result if the null hypothesis were true. So a p value of .02 means that if the null hypothesis were true, a sample result this extreme would occur only 2% of the time.
You can avoid this misunderstanding by remembering that the p value is not the probability that any particular hypothesis is true or false. Instead, it is the probability of obtaining the sample result if the null hypothesis were true.
Role of Sample Size and Relationship Strength
Recall that null hypothesis testing involves answering the question, “If the null hypothesis were true, what is the probability of a sample result as extreme as this one?” In other words, “What is the p value?” It can be helpful to see that the answer to this question depends on just two considerations: the strength of the relationship and the size of the sample. Specifically, the stronger the sample relationship and the larger the sample, the less likely the result would be if the null hypothesis were true. That is, the lower the p value. This should make sense. Imagine a study in which a sample of 500 women is compared with a sample of 500 men in terms of some psychological characteristic, and Cohen’s d is a strong 0.50. If there were really no sex difference in the population, then a result this strong based on such a large sample should seem highly unlikely. Now imagine a similar study in which a sample of three women is compared with a sample of three men, and Cohen’s d is a weak 0.10. If there were no sex difference in the population, then a relationship this weak based on such a small sample should seem likely. And this is precisely why the null hypothesis would be rejected in the first example and retained in the second.
Of course, sometimes the result can be weak and the sample large, or the result can be strong and the sample small. In these cases, the two considerations trade off against each other so that a weak result can be statistically significant if the sample is large enough and a strong relationship can be statistically significant even if the sample is small. Table 13.1 “How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant” shows roughly how relationship strength and sample size combine to determine whether a sample result is statistically significant. The columns of the table represent the three levels of relationship strength: weak, medium, and strong. The rows represent four sample sizes that can be considered small, medium, large, and extra large in the context of psychological research. Thus each cell in the table represents a combination of relationship strength and sample size. If a cell contains the word Yes , then this combination would be statistically significant for both Cohen’s d and Pearson’s r . If it contains the word No , then it would not be statistically significant for either. There is one cell where the decision for d and r would be different and another where it might be different depending on some additional considerations, which are discussed in Section 13.2 “Some Basic Null Hypothesis Tests”
Table 13.1 How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant
| Relationship strength | |||
|---|---|---|---|
| Sample Size | Weak | Medium | Strong |
| Small ( = 20) | No | No | = Maybe = Yes |
| Medium ( = 50) | No | Yes | Yes |
| Large ( = 100) | = Yes = No | Yes | Yes |
| Extra large ( = 500) | Yes | Yes | Yes |
Although Table 13.1 “How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant” provides only a rough guideline, it shows very clearly that weak relationships based on medium or small samples are never statistically significant and that strong relationships based on medium or larger samples are always statistically significant. If you keep this in mind, you will often know whether a result is statistically significant based on the descriptive statistics alone. It is extremely useful to be able to develop this kind of intuitive judgment. One reason is that it allows you to develop expectations about how your formal null hypothesis tests are going to come out, which in turn allows you to detect problems in your analyses. For example, if your sample relationship is strong and your sample is medium, then you would expect to reject the null hypothesis. If for some reason your formal null hypothesis test indicates otherwise, then you need to double-check your computations and interpretations. A second reason is that the ability to make this kind of intuitive judgment is an indication that you understand the basic logic of this approach in addition to being able to do the computations.
Statistical Significance Versus Practical Significance
Table 13.1 “How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant” illustrates another extremely important point. A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is closely related to Janet Shibley Hyde’s argument about sex differences (Hyde, 2007). The differences between women and men in mathematical problem solving and leadership ability are statistically significant. But the word significant can cause people to interpret these differences as strong and important—perhaps even important enough to influence the college courses they take or even who they vote for. As we have seen, however, these statistically significant differences are actually quite weak—perhaps even “trivial.”
This is why it is important to distinguish between the statistical significance of a result and the practical significance of that result. Practical significance refers to the importance or usefulness of the result in some real-world context. Many sex differences are statistically significant—and may even be interesting for purely scientific reasons—but they are not practically significant. In clinical practice, this same concept is often referred to as “clinical significance.” For example, a study on a new treatment for social phobia might show that it produces a statistically significant positive effect. Yet this effect still might not be strong enough to justify the time, effort, and other costs of putting it into practice—especially if easier and cheaper treatments that work almost as well already exist. Although statistically significant, this result would be said to lack practical or clinical significance.
Key Takeaways
- Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance.
- The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favor of the alternative hypothesis. If it would not be unlikely, then the null hypothesis is retained.
- The probability of obtaining the sample result if the null hypothesis were true (the p value) is based on two considerations: relationship strength and sample size. Reasonable judgments about whether a sample relationship is statistically significant can often be made by quickly considering these two factors.
- Statistical significance is not the same as relationship strength or importance. Even weak relationships can be statistically significant if the sample size is large enough. It is important to consider relationship strength and the practical significance of a result in addition to its statistical significance.
- Discussion: Imagine a study showing that people who eat more broccoli tend to be happier. Explain for someone who knows nothing about statistics why the researchers would conduct a null hypothesis test.
Practice: Use Table 13.1 “How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant” to decide whether each of the following results is statistically significant.
- The correlation between two variables is r = −.78 based on a sample size of 137.
- The mean score on a psychological characteristic for women is 25 ( SD = 5) and the mean score for men is 24 ( SD = 5). There were 12 women and 10 men in this study.
- In a memory experiment, the mean number of items recalled by the 40 participants in Condition A was 0.50 standard deviations greater than the mean number recalled by the 40 participants in Condition B.
- In another memory experiment, the mean scores for participants in Condition A and Condition B came out exactly the same!
- A student finds a correlation of r = .04 between the number of units the students in his research methods class are taking and the students’ level of stress.
Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003.
Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science , 16 , 259–263.
Research Methods in Psychology Copyright © 2016 by University of Minnesota is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
- School Guide
- Mathematics
- Number System and Arithmetic
- Trigonometry
- Probability
- Mensuration
- Maths Formulas
- Integration Formulas
- Differentiation Formulas
- Trigonometry Formulas
- Algebra Formulas
- Mensuration Formula
- Statistics Formulas
- Trigonometric Table
Null Hypothesis
Null Hypothesis , often denoted as H 0, is a foundational concept in statistical hypothesis testing. It represents an assumption that no significant difference, effect, or relationship exists between variables within a population. It serves as a baseline assumption, positing no observed change or effect occurring. The null is t he truth or falsity of an idea in analysis.
In this article, we will discuss the null hypothesis in detail, along with some solved examples and questions on the null hypothesis.
Table of Content
What is Null Hypothesis?
Null hypothesis symbol, formula of null hypothesis, types of null hypothesis, null hypothesis examples, principle of null hypothesis, how do you find null hypothesis, null hypothesis in statistics, null hypothesis and alternative hypothesis, null hypothesis and alternative hypothesis examples, null hypothesis – practice problems.
Null Hypothesis in statistical analysis suggests the absence of statistical significance within a specific set of observed data. Hypothesis testing, using sample data, evaluates the validity of this hypothesis. Commonly denoted as H 0 or simply “null,” it plays an important role in quantitative analysis, examining theories related to markets, investment strategies, or economies to determine their validity.
Null Hypothesis Meaning
Null Hypothesis represents a default position, often suggesting no effect or difference, against which researchers compare their experimental results. The Null Hypothesis, often denoted as H 0 asserts a default assumption in statistical analysis. It posits no significant difference or effect, serving as a baseline for comparison in hypothesis testing.
The null Hypothesis is represented as H 0 , the Null Hypothesis symbolizes the absence of a measurable effect or difference in the variables under examination.
Certainly, a simple example would be asserting that the mean score of a group is equal to a specified value like stating that the average IQ of a population is 100.
The Null Hypothesis is typically formulated as a statement of equality or absence of a specific parameter in the population being studied. It provides a clear and testable prediction for comparison with the alternative hypothesis. The formulation of the Null Hypothesis typically follows a concise structure, stating the equality or absence of a specific parameter in the population.
Mean Comparison (Two-sample t-test)
H 0 : μ 1 = μ 2
This asserts that there is no significant difference between the means of two populations or groups.
Proportion Comparison
H 0 : p 1 − p 2 = 0
This suggests no significant difference in proportions between two populations or conditions.
Equality in Variance (F-test in ANOVA)
H 0 : σ 1 = σ 2
This states that there’s no significant difference in variances between groups or populations.
Independence (Chi-square Test of Independence):
H 0 : Variables are independent
This asserts that there’s no association or relationship between categorical variables.
Null Hypotheses vary including simple and composite forms, each tailored to the complexity of the research question. Understanding these types is pivotal for effective hypothesis testing.
Equality Null Hypothesis (Simple Null Hypothesis)
The Equality Null Hypothesis, also known as the Simple Null Hypothesis, is a fundamental concept in statistical hypothesis testing that assumes no difference, effect or relationship between groups, conditions or populations being compared.
Non-Inferiority Null Hypothesis
In some studies, the focus might be on demonstrating that a new treatment or method is not significantly worse than the standard or existing one.
Superiority Null Hypothesis
The concept of a superiority null hypothesis comes into play when a study aims to demonstrate that a new treatment, method, or intervention is significantly better than an existing or standard one.
Independence Null Hypothesis
In certain statistical tests, such as chi-square tests for independence, the null hypothesis assumes no association or independence between categorical variables.
Homogeneity Null Hypothesis
In tests like ANOVA (Analysis of Variance), the null hypothesis suggests that there’s no difference in population means across different groups.
- Medicine: Null Hypothesis: “No significant difference exists in blood pressure levels between patients given the experimental drug versus those given a placebo.”
- Education: Null Hypothesis: “There’s no significant variation in test scores between students using a new teaching method and those using traditional teaching.”
- Economics: Null Hypothesis: “There’s no significant change in consumer spending pre- and post-implementation of a new taxation policy.”
- Environmental Science: Null Hypothesis: “There’s no substantial difference in pollution levels before and after a water treatment plant’s establishment.”
The principle of the null hypothesis is a fundamental concept in statistical hypothesis testing. It involves making an assumption about the population parameter or the absence of an effect or relationship between variables.
In essence, the null hypothesis (H 0 ) proposes that there is no significant difference, effect, or relationship between variables. It serves as a starting point or a default assumption that there is no real change, no effect or no difference between groups or conditions.
Null Hypothesis Rejection
Rejecting the Null Hypothesis occurs when statistical evidence suggests a significant departure from the assumed baseline. It implies that there is enough evidence to support the alternative hypothesis, indicating a meaningful effect or difference. Null Hypothesis rejection occurs when statistical evidence suggests a deviation from the assumed baseline, prompting a reconsideration of the initial hypothesis.
Identifying the Null Hypothesis involves defining the status quotient, asserting no effect and formulating a statement suitable for statistical analysis.
When is Null Hypothesis Rejected?
The Null Hypothesis is rejected when statistical tests indicate a significant departure from the expected outcome, leading to the consideration of alternative hypotheses. It occurs when statistical evidence suggests a deviation from the assumed baseline, prompting a reconsideration of the initial hypothesis.
In statistical hypothesis testing, researchers begin by stating the null hypothesis, often based on theoretical considerations or previous research. The null hypothesis is then tested against an alternative hypothesis (Ha), which represents the researcher’s claim or the hypothesis they seek to support.
The process of hypothesis testing involves collecting sample data and using statistical methods to assess the likelihood of observing the data if the null hypothesis were true. This assessment is typically done by calculating a test statistic, which measures the difference between the observed data and what would be expected under the null hypothesis.
In the realm of hypothesis testing, the null hypothesis (H 0 ) and alternative hypothesis (H₁ or Ha) play critical roles. The null hypothesis generally assumes no difference, effect, or relationship between variables, suggesting that any observed change or effect is due to random chance. Its counterpart, the alternative hypothesis, asserts the presence of a significant difference, effect, or relationship between variables, challenging the null hypothesis. These hypotheses are formulated based on the research question and guide statistical analyses.
Difference Between Null Hypothesis and Alternative Hypothesis
The null hypothesis (H 0 ) serves as the baseline assumption in statistical testing, suggesting no significant effect, relationship, or difference within the data. It often proposes that any observed change or correlation is merely due to chance or random variation. Conversely, the alternative hypothesis (H 1 or Ha) contradicts the null hypothesis, positing the existence of a genuine effect, relationship or difference in the data. It represents the researcher’s intended focus, seeking to provide evidence against the null hypothesis and support for a specific outcome or theory. These hypotheses form the crux of hypothesis testing, guiding the assessment of data to draw conclusions about the population being studied.
Criteria | Null Hypothesis | Alternative Hypothesis |
|---|---|---|
Definition | Assumes no effect or difference | Asserts a specific effect or difference |
Symbol | H | H (or Ha) |
Formulation | States equality or absence of parameter | States a specific value or relationship |
Testing Outcome | Rejected if evidence of a significant effect | Accepted if evidence supports the hypothesis |
Let’s envision a scenario where a researcher aims to examine the impact of a new medication on reducing blood pressure among patients. In this context:
Null Hypothesis (H 0 ): “The new medication does not produce a significant effect in reducing blood pressure levels among patients.”
Alternative Hypothesis (H 1 or Ha): “The new medication yields a significant effect in reducing blood pressure levels among patients.”
The null hypothesis implies that any observed alterations in blood pressure subsequent to the medication’s administration are a result of random fluctuations rather than a consequence of the medication itself. Conversely, the alternative hypothesis contends that the medication does indeed generate a meaningful alteration in blood pressure levels, distinct from what might naturally occur or by random chance.
People Also Read:
Mathematics Maths Formulas Probability and Statistics
Example 1: A researcher claims that the average time students spend on homework is 2 hours per night.
Null Hypothesis (H 0 ): The average time students spend on homework is equal to 2 hours per night. Data: A random sample of 30 students has an average homework time of 1.8 hours with a standard deviation of 0.5 hours. Test Statistic and Decision: Using a t-test, if the calculated t-statistic falls within the acceptance region, we fail to reject the null hypothesis. If it falls in the rejection region, we reject the null hypothesis. Conclusion: Based on the statistical analysis, we fail to reject the null hypothesis, suggesting that there is not enough evidence to dispute the claim of the average homework time being 2 hours per night.
Example 2: A company asserts that the error rate in its production process is less than 1%.
Null Hypothesis (H 0 ): The error rate in the production process is 1% or higher. Data: A sample of 500 products shows an error rate of 0.8%. Test Statistic and Decision: Using a z-test, if the calculated z-statistic falls within the acceptance region, we fail to reject the null hypothesis. If it falls in the rejection region, we reject the null hypothesis. Conclusion: The statistical analysis supports rejecting the null hypothesis, indicating that there is enough evidence to dispute the company’s claim of an error rate of 1% or higher.
Q1. A researcher claims that the average time spent by students on homework is less than 2 hours per day. Formulate the null hypothesis for this claim?
Q2. A manufacturing company states that their new machine produces widgets with a defect rate of less than 5%. Write the null hypothesis to test this claim?
Q3. An educational institute believes that their online course completion rate is at least 60%. Develop the null hypothesis to validate this assertion?
Q4. A restaurant claims that the waiting time for customers during peak hours is not more than 15 minutes. Formulate the null hypothesis for this claim?
Q5. A study suggests that the mean weight loss after following a specific diet plan for a month is more than 8 pounds. Construct the null hypothesis to evaluate this statement?
Summary – Null Hypothesis and Alternative Hypothesis
The null hypothesis (H 0 ) and alternative hypothesis (H a ) are fundamental concepts in statistical hypothesis testing. The null hypothesis represents the default assumption, stating that there is no significant effect, difference, or relationship between variables. It serves as the baseline against which the alternative hypothesis is tested. In contrast, the alternative hypothesis represents the researcher’s hypothesis or the claim to be tested, suggesting that there is a significant effect, difference, or relationship between variables. The relationship between the null and alternative hypotheses is such that they are complementary, and statistical tests are conducted to determine whether the evidence from the data is strong enough to reject the null hypothesis in favor of the alternative hypothesis. This decision is based on the strength of the evidence and the chosen level of significance. Ultimately, the choice between the null and alternative hypotheses depends on the specific research question and the direction of the effect being investigated.
FAQs on Null Hypothesis
What does null hypothesis stands for.
The null hypothesis, denoted as H 0 , is a fundamental concept in statistics used for hypothesis testing. It represents the statement that there is no effect or no difference, and it is the hypothesis that the researcher typically aims to provide evidence against.
How to Form a Null Hypothesis?
A null hypothesis is formed based on the assumption that there is no significant difference or effect between the groups being compared or no association between variables being tested. It often involves stating that there is no relationship, no change, or no effect in the population being studied.
When Do we reject the Null Hypothesis?
In statistical hypothesis testing, if the p-value (the probability of obtaining the observed results) is lower than the chosen significance level (commonly 0.05), we reject the null hypothesis. This suggests that the data provides enough evidence to refute the assumption made in the null hypothesis.
What is a Null Hypothesis in Research?
In research, the null hypothesis represents the default assumption or position that there is no significant difference or effect. Researchers often try to test this hypothesis by collecting data and performing statistical analyses to see if the observed results contradict the assumption.
What Are Alternative and Null Hypotheses?
The null hypothesis (H0) is the default assumption that there is no significant difference or effect. The alternative hypothesis (H1 or Ha) is the opposite, suggesting there is a significant difference, effect or relationship.
What Does it Mean to Reject the Null Hypothesis?
Rejecting the null hypothesis implies that there is enough evidence in the data to support the alternative hypothesis. In simpler terms, it suggests that there might be a significant difference, effect or relationship between the groups or variables being studied.
How to Find Null Hypothesis?
Formulating a null hypothesis often involves considering the research question and assuming that no difference or effect exists. It should be a statement that can be tested through data collection and statistical analysis, typically stating no relationship or no change between variables or groups.
How is Null Hypothesis denoted?
The null hypothesis is commonly symbolized as H 0 in statistical notation.
What is the Purpose of the Null hypothesis in Statistical Analysis?
The null hypothesis serves as a starting point for hypothesis testing, enabling researchers to assess if there’s enough evidence to reject it in favor of an alternative hypothesis.
What happens if we Reject the Null hypothesis?
Rejecting the null hypothesis implies that there is sufficient evidence to support an alternative hypothesis, suggesting a significant effect or relationship between variables.
What are Test for Null Hypothesis?
Various statistical tests, such as t-tests or chi-square tests, are employed to evaluate the validity of the Null Hypothesis in different scenarios.
Please Login to comment...
Similar reads.
- Geeks Premier League
- School Learning
- Geeks Premier League 2023
- Math-Concepts
- Top 10 Fun ESL Games and Activities for Teaching Kids English Abroad in 2024
- Top Free Voice Changers for Multiplayer Games and Chat in 2024
- Best Monitors for MacBook Pro and MacBook Air in 2024
- 10 Best Laptop Brands in 2024
- System Design Netflix | A Complete Architecture
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
Pardon Our Interruption
As you were browsing something about your browser made us think you were a bot. There are a few reasons this might happen:
- You've disabled JavaScript in your web browser.
- You're a power user moving through this website with super-human speed.
- You've disabled cookies in your web browser.
- A third-party browser plugin, such as Ghostery or NoScript, is preventing JavaScript from running. Additional information is available in this support article .
To regain access, please make sure that cookies and JavaScript are enabled before reloading the page.

IMAGES
VIDEO
COMMENTS
If the collected data does not meet the expectation of the null hypothesis, a researcher can conclude that the data lacks sufficient evidence to back up the null hypothesis, and thus the null hypothesis is rejected. Rejecting the null hypothesis means that a relationship does exist between a set of variables and the effect is statistically ...
A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis. We always use the following steps to perform a hypothesis test: Step 1: State the null and alternative hypotheses. The null hypothesis, denoted as H0, is the hypothesis that the sample data occurs purely from chance.
Reject the null hypothesis when the p-value is less than or equal to your significance level. Your sample data favor the alternative hypothesis, which suggests that the effect exists in the population. For a mnemonic device, remember—when the p-value is low, the null must go! ... Null Hypothesis H 0: Group means are equal in the population: ...
so, that's why when p<0.01 we reject the null hypothesis, because it's too rare (p0.05, i can understand that for most cases we cannot accept the null, for example, if p=0.5, it means that the probability to get a statistic from the distribution is 0.5, which is totally random.
Key Takeaways: The Null Hypothesis. • In a test of significance, the null hypothesis states that there is no meaningful relationship between two measured phenomena. • By comparing the null hypothesis to an alternative hypothesis, scientists can either reject or fail to reject the null hypothesis. • The null hypothesis cannot be positively ...
Let's return finally to the question of whether we reject or fail to reject the null hypothesis. If our statistical analysis shows that the significance level is below the cut-off value we have set (e.g., either 0.05 or 0.01), we reject the null hypothesis and accept the alternative hypothesis. Alternatively, if the significance level is above ...
Alternative hypothesis. Alternative hypothesis \(\left(H_{A}\right)\): If we conclude that the null hypothesis is false, or rather and more precisely, we find that we provisionally fail to reject the null hypothesis, then we provisionally accept the alternative hypothesis.The view then is that something other than random chance has influenced the sample observations.
A possible null hypothesis is that the mean male score is the same as the mean female score: H 0: ... Rejection of the null hypothesis is not necessarily the real goal of a significance tester. An adequate statistical model may be associated with a failure to reject the null; the model is adjusted until the null is not rejected. ...
The null hypothesis (H0) answers "No, there's no effect in the population.". The alternative hypothesis (Ha) answers "Yes, there is an effect in the population.". The null and alternative are always claims about the population. That's because the goal of hypothesis testing is to make inferences about a population based on a sample.
A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value. A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A high p value means that the sample ...
The first step in hypothesis testing is to set up two competing hypotheses. The hypotheses are the most important aspect. If the hypotheses are incorrect, your conclusion will also be incorrect. The two hypotheses are named the null hypothesis and the alternative hypothesis. The null hypothesis is typically denoted as H 0.
Review. In a hypothesis test, sample data is evaluated in order to arrive at a decision about some type of claim.If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis, typically denoted with \(H_{0}\).The null is not rejected unless the hypothesis test shows otherwise.
When we reject the null, we know that the data has provided a lot of evidence against the null. In other words, it is unlikely (how unlikely depends on the size of the test) that the null is true given the data we have observed. There is an important caveat though. The null hypothesis is often made up of several assumptions, including:
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
As a hypothesis test, we could have the alternative hypothesis as H 1 ≠ 0.51. Since the null value of 0.51 lies within the confidence interval, then we would fail to reject the null hypothesis at ɑ = 0.05. On the other hand, if H 1 ≠ 0.61, then since 0.61 is not in the confidence interval we can reject the null hypothesis at ɑ = 0.05.
When the sample size becomes larger, point estimates become more precise and any real differences in the mean and null value become easier to detect and recognize. Even a very small difference would likely be detected if we took a large enough sample. ... Erroneously rejecting a true null hypothesis or erroneously failing to reject a false null ...
16.3.5 Step 5: Determine the probability of the data under the null hypothesis. This is the step where NHST starts to violate our intuition - rather than determining the likelihood that the null hypothesis is true given the data, we instead determine the likelihood of the data under the null hypothesis - because we started out by assuming that the null hypothesis is true!
x: The value of the predictor variable. Simple linear regression uses the following null and alternative hypotheses: H0: β1 = 0. HA: β1 ≠ 0. The null hypothesis states that the coefficient β1 is equal to zero. In other words, there is no statistically significant relationship between the predictor variable, x, and the response variable, y.
The most common null hypothesis test for this type of statistical relationship is the t test. In this section, we look at three types of t tests that are used for slightly different research designs: the one-sample t test, the dependent-samples t test, and the independent-samples t test. The one-sample t test is used to compare a sample mean (M ...
Therefore, they rejected the null hypothesis in favor of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population. ... This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to reject it. Researchers ...
Failing to reject the null hypothesis—that the results are explainable by chance alone—is a weak ... (calculated) sample mean to the (claimed) population mean (8%) to test the null hypothesis.
Traditionally, the null hypothesis is a point value. (It is typically $0$, but can in fact be any point value.) The alternative hypothesis is that the true value is any value other than the null value.Because a continuous variable (such as a mean difference) can take on a value which is indefinitely close to the null value but still not quite equal and thus make the null hypothesis false, a ...
A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value. A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A high p value means that the sample ...
H A: At least one group mean is different from the rest; Since the p-value from the ANOVA table is not less than 0.05, we fail to reject the null hypothesis. This means we don't have sufficient evidence to say that there is a statistically significant difference between the mean exam scores of the three groups. Example 2: Two-Way ANOVA
Null hypothesis, often denoted as H0, is a foundational concept in statistical hypothesis testing. It represents an assumption that no significant difference, effect, or relationship exists between variables within a population. Learn more about Null Hypothesis, its formula, symbol and example in this article
Suppose that for a random sample of 60 Buffalo residents the mean is 22.6 miles a day and the standard deviation 8.2 is miles a day, ... Formulate hypotheses so that, if the null hypothesis is rejected, we can conclude that salaries for Finance majors are significantly lower than the salaries of Business Analytics majors. Use α = .05 . Ho: ...