Reset password New user? Sign up
Existing user? Log in

Semidirect product
Already have an account? Log in here.
In group theory , a semidirect product is a generalization of the direct product which expresses a group as a product of subgroups .
There are two ways to think of the construction. One is intrinsic: the condition that a given group \(G\) is a semidirect product of two given subgroups \(N\) and \(H\) is equivalent to some special conditions on the subgroups. This concept is usually called an inner semidirect product : \(G = N \rtimes H.\) Expressing a group \(G\) as an inner semidirect product of two subgroups can help in the study of the group's behavior. It can also help classify \(G\) up to isomorphism .
Another way to think of semidirect products is extrinsic: given two abstract groups \(G_1,G_2\) with some specified relationship between them, given by a certain homomorphism \(\phi\) (as defined below), one can construct a new group called the semidirect product (or outer semidirect product ) \(G = G_1 \rtimes_\phi G_2.\) In this way, one can build new, larger groups from smaller ones, with a construction that is more general and richer than a direct product.
Inner semidirect product
Outer semidirect product, proof of the theorem.
The following theorem gives three equivalent definitions of an inner semidirect product.
Let \(G\) be a group and let \(N\) and \(H\) be subgroups of \(G,\) with \(N\) normal. Then the following statements are equivalent: \(NH = G\) and \( N \cap H = \{1\}.\) Every \(g \in G\) can be written uniquely as \(g = nh\) with \(n \in N, h \in H.\) Define \( \psi : H \to G/N\) in the natural way: \(\psi(h) = {\overline{h}} = hN.\) Then \(\psi\) is an isomorphism. If these conditions hold, one writes \(G = N \rtimes H\) and says that this expresses \(G\) as an inner semidirect product of \(N\) and \(H.\)
Note that \(N\) must be normal for these statements to make sense.
The proof of the theorem is straightforward: see the last section of the wiki.
Let \(G = S_3.\) Let \(N\) be the normal subgroup of order 3 generated by a 3-cycle, and let \(H\) be a subgroup of order 2 generated by a 2-cycle. Then \(G = N \rtimes H\) (e.g. by condition (1)). This example generalizes along two different lines: first, let \(G = S_n,\) \(N = A_n,\) \(H\) a subgroup of order 2 generated by a 2-cycle. Then \(G = N \rtimes H\) in exactly the same way. Second, let \(G = D_n,\) the dihedral group of order \(2n.\) Then let \(N\) be the index-2 subgroup generated by rotations of the \(n\)-gon, and let \(H\) be an order-2 subgroup generated by a reflection. Then \(G = N \rtimes H.\)
In verifying that a group \(G\) is a semi-direct product of two given subgroups, it is often useful to note that if \(G\) is finite and \(|N| \cdot |H| = |G|,\) then it suffices to check exactly one of the two conditions \(NH = G\) and \(N \cap H = \{1\}\) (e.g. by the Second Isomorphism Theorem ). And further, if \(|N|\) and \(|H|\) are relatively prime and \(|N| \cdot |H| = |G|,\) the condition \(N \cap H = \{1\}\) is automatic by Lagrange's theorem , so both conditions hold automatically.
Let \(G\) be a group of order \(p^a q^b\) for distinct primes \(p,q.\) Let \(N\) be its Sylow \(p\)-subgroup and suppose that \(N\) is normal. Show that \(G = N \rtimes H\) for some subgroup \(H.\) Let \(H\) be a Sylow \(q\)-subgroup. Then \(|N| \cdot |H| = |G|\) and \(|N|\) and \(|H|\) are coprime, so the above remarks show immediately that \(G = N \rtimes H.\)
The outer semidirect product is a sort of generalization of the inner semidirect product. Instead of starting with \(G\) and prescribed subgroups \(N\) and \(H,\) the outer semidirect product starts only with the abstract subgroups and constructs the semidirect product \(G.\) The construction does require a notion of multiplication of elements of \(N\) with elements of \(H\); this extra structure is part of the data that is used to construct the group \(G.\)
Let \(N\) and \(H\) be groups, and suppose \(\phi : H \to \text{Aut}(N)\) is a homomorphism, which sends elements \(h \in H\) to automorphisms \(\phi_h\) of \(N.\) Then the group \(G = N \rtimes_\phi H\) is defined as the set of ordered pairs \((n,h)\) with \(n \in N, h \in H,\) and group law given by the formula \[ (n,h) \cdot (n_1,h_1) = (n\phi_h(n_1),hh_1). \]
The verification that \(G\) is a group is nontrivial but straightforward.
Note that the group \(G\) depends very strongly on the homomorphism \(\phi.\) Leaving \(H\) and \(N\) unchanged but changing \(\phi\) will change the group \(G\) (even up to isomorphism--two different \(\phi\) can lead to two non-isomorphic groups \(G\)).
Note that this group law is a sort of "twisted" version of the group law of the direct product. Another way to say this is that direct products are trivial examples of semidirect products:
If \(N\) and \(H\) are any groups, and \(\phi : H \to \text{Aut}(N)\) is the trivial homomorphism, sending every \(h\in H\) to the identity automorphism of \(N,\) then \(N \rtimes_\phi H = N \times H.\)
An outer semidirect product is an inner semidirect product. That is, given \(N,\) \(H,\) and a homomorphism \(\phi : H \to \text{Aut}(N),\) the group \( G = N \rtimes_\phi H\) has a normal subgroup \({\mathcal N} = \{ (n,1) : n \in N\}\) and a subgroup \({\mathcal H} = \{(1,h) : h \in H\},\) such that \(G = {\mathcal N} \rtimes {\mathcal H}.\) (Of course \({\mathcal N} \cong N\) and \({\mathcal H} \cong H.\))
An inner semidirect product is an outer semidirect product. That is, given a group \(G\) with subgroups \(N\) and \(H\) such that \(G = N \rtimes H,\) there is a natural homomorphism \(\phi : H \to \text{Aut}(N)\) such that \(G \cong N \rtimes_\phi H.\) That homomorphism is as follows: for \(h \in H,\) define \(\phi_h(n) = hnh^{-1}.\) Then \[ n_1h_1n_2h_2 = n_1 (h_1n_2h_1^{-1}) h_1h_2 = (n_1\phi_{h_1}(n_2))(h_1h_2), \] which looks like the group law for an outer semidirect product; in other words, the above computation shows that the bijection \(G \to N \rtimes_\phi H\) defined by \(nh \mapsto (n,h)\) is also a homomorphism.
Let \(N\) and \(H\) be groups, let \(\phi : H \to \text{Aut}(N)\) be a homomorphism, and let \(G = N \rtimes_\phi H\) be the (outer) semidirect product. Suppose that \(G\) is abelian. Which of the following three statements must necessarily be true about \(H,N,\phi\)?
I. \(H\) and \(N\) are abelian
II. \(\phi\) is the trivial homomorphism
III. \(G\) is actually a direct product of groups
Let \(N = {\mathbb Z}_2 \times {\mathbb Z}_2\) and let \(H = {\mathbb Z}_2.\) Consider the automorphism \(\phi: H \to \text{Aut}(N)\) which sends the nontrivial element of \(H\) to the homomorphism \((a,b) \mapsto (b,a).\) Then the group \(N \rtimes_\phi H\) is a group of order 8. Which group of order 8 is it isomorphic to? The most illuminating way to show that \(G\) is isomorphic to the dihedral group \(D_4\) is to find subgroups isomorphic to \(N\) and \(H\) in \(G\) such that the conjugation action of \(H\) on \(N\) is the same as the effect of \(\phi.\) Let \(\sigma\) be a 90-degree rotation and \(\tau\) a reflection. Then \(\sigma^4 = \tau^2 = 1\) and \(\sigma\tau = \tau \sigma^{-1}.\) Let \(N = \{ 1, \sigma^2, \tau, \sigma^2 \tau \}\) and let \(H = \{1,\sigma \tau\}.\) Then \(N \cong {\mathbb Z}_2 \times {\mathbb Z}_2\) and \(H \cong {\mathbb Z}_2,\) as desired. What does conjugation by the nontrivial element of \(H\) do to \(N\)? It sends \( \tau \) to \(\sigma^2 \tau\) and vice versa, and fixes \(1\) and \(\sigma^2.\) Picking the isomorphism \(N \cong {\mathbb Z}_2 \times {\mathbb Z}_2\) that sends \( \tau\) and \(\sigma^2\tau\) to \((1,0)\) and \((0,1)\) respectively, we see that conjugation by \(H\) has the effect of switching \((1,0)\) and \((0,1)\) and preserving \((0,0)\) and \((1,1),\) which is precisely the automorphism \(\phi_h.\)
Note that this gives an example of the phenomenon mentioned above, that different choices of \(\phi\) can lead to nonisomorphic groups: if \(\phi\) is chosen to be the trivial homomorphism, then \(N \rtimes_\phi H \cong N \times H = {\mathbb Z}_2 \times {\mathbb Z}_2 \times {\mathbb Z}_2.\)
Let \[ G = \left\{ \begin{pmatrix} a&b\\0&1 \end{pmatrix} : a,b \in {\mathbb R}, a \ne 0 \right\}, \] with group operation given by matrix multiplication. Let \(H\) be the subgroup of \(G\) consisting of diagonal matrices \(\begin{pmatrix} a&0 \\ 0 &1 \end{pmatrix},\) and let \(N\) be the subgroup of \(G\) consisting of matrices of the form \(\begin{pmatrix} 1&b\\0&1 \end{pmatrix}.\) Then \(N\) is normal, \(NH = G,\) and \(N \cap H = \{1\},\) so \(G = N \rtimes H.\) Abstractly, \(N \cong {\mathbb R}\) and \(H \cong {\mathbb R}^*\), so \(G\) is isomorphic to the (outer) semidirect product \({\mathbb R} \rtimes_\phi {\mathbb R}^*,\) where \(\phi\) sends a nonzero real number \(h\) to the automorphism of the additive group \(\mathbb R\) given by multiplication by \(h.\) Another way to view \(G\) is as a group of affine transformations \(x \mapsto ax+b.\) Then matrix multiplication in \(G\) corresponds to composition of the associated affine transformations.
\( (1) \Rightarrow (2):\) Since \(NH = G,\) every \(g\) can be written as \(g=nh.\) The representation is unique because, if \(nh = n_1h_1,\) then \(n_1^{-1} n = h_1 h^{-1}.\) The left side is in \(N\) and the right side is in \(H\); since \(N \cap H = \{1\}\) they must both be \(1,\) so \(n_1 = n\) and \(h_1 = h.\) \( (2) \Rightarrow (3):\) To see that \(\psi\) is surjective, note that any coset \(gN\) can be rewritten using (2) as \(nhN = h(h^{-1}nh)N = hN,\) for some \(n\in N, h \in H.\) (This is because \(h^{-1}nh \in N,\) because \(N\) is normal.) To see that \(\psi\) is injective, suppose \(h \in \text{ker}(\psi).\) Then \(h \in N,\) but then \(h = h \cdot 1 = 1 \cdot h\) expresses \(h\) in two ways as a product of an element in \(N\) and an element in \(H.\) This representation is supposed to be unique, so \(h\) must equal \(1.\) \( (3) \Rightarrow (1):\) If \(h \in N \cap H,\) then \(\psi(h) = hN = N\) is the identity of \(G/N,\) so \(h = 1\) because \(\psi\) is injective. Now for any \(g \in G,\) \(gN = hN\) for some \(h \in H\) because \(\psi\) is surjective. So \(g \in hN,\) so \(g = hn\) for some \(n \in N,\) so \(g = (hnh^{-1})h \in NH.\) This shows that \(NH = G.\)
Problem Loading...
Note Loading...
Set Loading...
Semidirect Product
Explore with Wolfram|Alpha
More things to try:
- .1234 with the last 2 digits repeating
- codes that can detect 10 errors
- int e^(-t^2) dt, t=-infinity to infinity
Referenced on Wolfram|Alpha
Cite this as:.
Weisstein, Eric W. "Semidirect Product." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/SemidirectProduct.html
Subject classifications
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Calculating presentations for the normal subgroup of a semidirect product
Let $G$ be a group with a finite presentation $\langle S \cup S' | R \cup R'\rangle$. Assume that I happen to know that $G$ is the semidirect product of a normal subgroup $N$ and another subgroup $H$. Furthermore, assume that $H$ is the subgroup generated by $S'$ and that $H \cong \langle S' | R' \rangle$. Is there any algorithm to calculate a presentation for $N$? Assume that we know how to solve all the standard problems (the word problem, the conjugacy problem, the membership problem for $H$ and $N$, etc) in $G$ itself.
Here is an easy example to show what kinds of issues arise. Let $G$ be the free group on two letters $x$ and $y$. We then have a split short exact sequence
$$1 \rightarrow N \rightarrow G \rightarrow H \rightarrow 1,$$
where the group $H$ is the cyclic group generated by $y$ and $N$ is an infinite rank free group (it consists of all words in $x$ and $y$ the sum of whose $y$-exponents is $0$). The moral is that we cannot hope for a finite presentation for $N$, and our algorithm must return an infinite presentation.
EDIT : Here's two nice examples of what I am talking about. First, let $G = PSL_2(\mathbb{Z})$ and let $H = PSL_2(\mathbb{Z}/2\mathbb{Z})$. Then it turns out that $H$ is isomorphic to the symmetric group on $3$ letters and there is a splitting of the natural surjection $G \rightarrow H$. How can one compute the kernel of this map?
For another example, let $G = SP_4(\mathbb{Z})$ and let $H = SP_4(\mathbb{Z}/2\mathbb{Z})$. Then $H$ is isomorphic to the symmetric group on $6$ letters (this comes from the action on odd theta characteristics), and there is a splitting of the homomorphism $G \rightarrow H$. How can one compute the kernel of this map?
As you might guess from these examples, I have in mind applications to the theory of modular forms. I am looking for practical algorithms for computation, not theoretical results.
- gr.group-theory
- $\begingroup$ If you are allowing infinite presentations, can't you just take elements of G as generators, with relations defined by the multiplication table, together with additional relations sending anything to zero if its image in H is not the identity? $\endgroup$ – S. Carnahan ♦ Commented Apr 9, 2010 at 4:38
- $\begingroup$ I'm not sure I follow. There is not necessarily a homomorphism from G to N -- remember, H does not need to be normal. What kinds of relations are you talking about? $\endgroup$ – Ian Brown Commented Apr 9, 2010 at 4:39
- $\begingroup$ A related comment -- the category of groups has the funny property that a splitting H->G of a short exact sequence 1-->N-->G-->H-->1 does not imply that there is a retract homomorphism G-->N. $\endgroup$ – Ian Brown Commented Apr 9, 2010 at 4:42
- $\begingroup$ My mistake. Instead, could you take all elements of G that map to the identity of H as generators, with multiplication in G defining relations? $\endgroup$ – S. Carnahan ♦ Commented Apr 9, 2010 at 4:42
- $\begingroup$ I think the real question I should be asking is, what is your model of computation, so that we can distinguish between silly algorithms like mine (assuming I didn't mess up again) and something that would be useful to you? $\endgroup$ – S. Carnahan ♦ Commented Apr 9, 2010 at 4:45
If you have explicit finite presentations of G and H is small and finite, then you should be able to just ask GAP or magma for a presentation of the kernel of the projection. This is another disguise of the Schreier transversal. Let me know if you want code sample or algorithmic references. This will likely fail for things like Sp(6,13) which are simply too large, but I think it should work out for Sym(3) and Sym(6).
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged gr.group-theory or ask your own question .
- Featured on Meta
- We've made changes to our Terms of Service & Privacy Policy - July 2024
- Announcing a change to the data-dump process
semidirect product of groups
Naturally, we start with the construction of semi–direct products.
Definition 1 .
For the remainder of this article, we omit θ from the notation whenever this map is clear from the context .
Theorem 2 .
Let G := H ⋊ Q as above. Then:
H Q = G .
H ∩ Q = { 1 G } .
Every ( h , q ) ∈ G can be written as ( h , 1 Q ) ( 1 H , q ) . Therefore H Q = G .
Finally, it is evident that ( 1 H , 1 Q ) is the only element of G that is of the form ( h , 1 Q ) for h ∈ H and ( 1 H , q ) for q ∈ Q . ∎
This result motivates the definition of internal semi–direct products.
Definition 3 .
Let G be a group with subgroups H and Q . We say G is the internal semi–direct product of H and Q if:
H is a normal subgroup of G .
Let G be a group with subgroups H and Q . Suppose G = H Q and H ∩ Q = { 1 G } . Then every element g of G can be written uniquely in the form h q , for h ∈ H and q ∈ Q .
Since G = H Q , we know that g can be written as h q . Suppose it can also be written as h ′ q ′ . Then h q = h ′ q ′ so h ′ - 1 h = q ′ q - 1 ∈ H ∩ Q = { 1 G } . Therefore h = h ′ and q = q ′ . ∎
Theorem 5 .
Suppose G is a group with subgroups H and Q , and G is the internal semi–direct product of H and Q . Then G ≅ H ⋊ θ Q where θ : Q ⟶ Aut ( H ) is given by
By Lemma 4 , every element g of G can be written uniquely in the form h q , with h ∈ H and q ∈ Q . Therefore, the map ϕ : H ⋊ Q ⟶ G given by ϕ ( h , q ) = h q is a bijection from G to H ⋊ Q . It only remains to show that this bijection is a homomorphism.
Given elements ( h , q ) and ( h ′ , q ′ ) in H ⋊ Q , we have
In summary, one may use Theorems 2 and 5 to pass freely between the notions of internal semi–direct product and external semi–direct product.
Finally, we discuss the correspondence between semi–direct products and split exact sequences of groups.
Definition 6 .
is split if there exists a homomorphism k : Q ⟶ G such that j ∘ k is the identity map on Q .
Theorem 7 .
Let G , H , and Q be groups. Then G is isomorphic to a semi–direct product H ⋊ Q if and only if there exists a split exact sequence
First suppose G ≅ H ⋊ Q . Let i : H ⟶ G be the inclusion map i ( h ) = ( h , 1 Q ) and let j : G ⟶ Q be the projection map j ( h , q ) = q . Let the splitting map k : Q ⟶ G be the inclusion map k ( q ) = ( 1 H , q ) . Then the sequence above is clearly split exact.
Now suppose we have the split exact sequence above. Let k : Q ⟶ G be the splitting map. Then:
i ( H ) = ker j , so i ( H ) is normal in G .
For any g ∈ G , set q := k ( j ( g ) ) . Then j ( g q - 1 ) = j ( g ) j ( k ( j ( g ) ) ) - 1 = 1 Q , so g q - 1 ∈ Im i . Set h := g q - 1 . Then g = h q . Therefore G = i ( H ) k ( Q ) .
Suppose g ∈ G is in both i ( H ) and k ( Q ) . Write g = k ( q ) . Then k ( q ) ∈ Im i = ker j , so q = j ( k ( q ) ) = 1 Q . Therefore g = k ( q ) = k ( 1 Q ) = 1 G , so i ( H ) ∩ k ( Q ) = { 1 G } .
This proves that G is the internal semi–direct product of i ( H ) and k ( Q ) . These are isomorphic to H and Q , respectively. Therefore G is isomorphic to a semi–direct product H ⋊ Q . ∎
Thus, not all normal subgroups H ⊂ G give rise to an (internal) semi–direct product G = H ⋊ G / H . More specifically, if H is a normal subgroup of G , we have the canonical exact sequence
We see that G can be decomposed into H ⋊ G / H as an internal semi–direct product if and only if the canonical exact sequence splits.
| Title | |
|---|---|
| Canonical name | SemidirectProductOfGroups |
| Date of creation | 2013-03-22 12:34:49 |
| Last modified on | 2013-03-22 12:34:49 |
| Owner | djao (24) |
| Last modified by | djao (24) |
| Numerical id | 10 |
| Author | djao (24) |
| Entry type | Definition |
| Classification | msc 20E22 |
| Synonym | |
| Synonym | semi-direct product |
Schwartz correspondence for real motion groups in low dimensions
- Open access
- Published: 29 July 2024
- Volume 66 , article number 5 , ( 2024 )
Cite this article
You have full access to this open access article

- Francesca Astengo 1 ,
- Bianca Di Blasio 2 &
- Fulvio Ricci 3
52 Accesses
Explore all metrics
For a Gelfand pair ( G , K ) with G a Lie group of polynomial growth and K a compact subgroup, the Schwartz correspondence states that the spherical transform maps the bi- K -invariant Schwartz space \({{\mathcal {S}}}(K\backslash G/K)\) isomorphically onto the space \({{\mathcal {S}}}(\Sigma _{{\mathcal {D}}})\) , where \(\Sigma _{{\mathcal {D}}}\) is an embedded copy of the Gelfand spectrum in \({{\mathbb {R}}}^\ell \) , canonically associated to a generating system \({{\mathcal {D}}}\) of G -invariant differential operators on G / K , and \({{\mathcal {S}}}(\Sigma _{{\mathcal {D}}})\) consists of restrictions to \(\Sigma _{{\mathcal {D}}}\) of Schwartz functions on \({{\mathbb {R}}}^\ell \) . Schwartz correspondence is known to hold for a large variety of Gelfand pairs of polynomial growth. In this paper we prove that it holds for the strong Gelfand pair \((M_n,SO_n)\) with \(n=3,4\) . The rather trivial case \(n=2\) is included in previous work by the same authors.
Similar content being viewed by others

Gelfand pairs admit an Iwasawa decomposition
Rigidity of some abelian-by-cyclic solvable group actions on $${\mathbb {t}}^n$$.
Self-Similar Groups and Holomorphic Dynamics: Renormalization, Integrability, and Spectrum
Avoid common mistakes on your manuscript.
1 Introduction
Let ( G , K ) be a Gelfand pair, with G a connected Lie group and K a compact subgroup of it. By definition, this means that the convolution algebra \(L^1(K\backslash G/K)\) of bi- K -invariant integrable functions on G , i.e. satisfying
is commutative, or, equivalently, that the composition algebra \({\mathbb {D}}(G/K)\) of G -invariant differential operators on G / K is commutative.
The Gelfand spectrum \(\Sigma \) of \(L^1(K\backslash G/K)\) is the space of bounded spherical functions on G with the topology induced by the weak* topology on \(L^\infty (K\backslash G/K)\) . For each choice of a finite generating subset \({\mathcal {D}}=\{D_1,\dots , D_\ell \}\) of \({\mathbb {D}}(G/K)\) , \(\Sigma \) can be homeomorphically embedded into \({\mathbb {C}}^\ell \) , by assigning to each spherical function \(\varphi \in \Sigma \) the \(\ell \) -tuple \(\xi =(\xi _1,\dots ,\xi _\ell )\) if \(D_j\varphi =\xi _j\varphi \) for \(j=1,\dots ,\ell \) . The image \(\Sigma _{\mathcal {D}}\) of this embedding is a closed subset of \({\mathbb {C}}^\ell \) [ 7 ].
Denoting by \(\varphi _\xi \) the spherical function associated with \(\xi \in \Sigma _{\mathcal {D}}\) , the spherical transform \({\mathcal {G}}f\) of \(f\in L^1(K\backslash G/K)\) can then be regarded as a map defined on \(\Sigma _{\mathcal {D}}\) by
If G has polynomial volume growth (in which case we also say that the pair ( G , K ) has polynomial growth) and the chosen generators \(D_j\in {\mathcal {D}}\) are symmetric, the eigenvalues are real, so that \(\Sigma _{\mathcal {D}}\subset {\mathbb {R}}^\ell \) . We refer to [ 3 ] for a presentation of Gelfand pairs of polynomial growth and the proofs of various preliminary results that will be used in this paper.
Gelfand pairs were originally introduced in the context of spherical analysis on symmetric spaces [ 12 ]. The interest in pairs of polynomial growth, and in particular of the nilpotent Gelfand pairs mentioned below, is more recent [ 5 , 6 , 13 , 14 , 15 , 19 , 22 , 23 , 24 ].
We say that Schwartz correspondence holds for a Gelfand pair ( G , K ) of polynomial growth if the following property is satisfied:
The spherical transform maps the bi- K -invariant Schwartz space \({\mathcal {S}}(K\backslash G/K)\) isomorphically onto the space \({\mathcal {S}}(\Sigma _{\mathcal {D}})\) of restrictions to \(\Sigma _{\mathcal {D}}\) of Schwartz functions on \({\mathbb {R}}^\ell \) .
This is an intrinsic property of the pair because it does not depend on the choice of the generating system \({\mathcal {D}}\) [ 2 , 3 , 9 ].
The range of Gelfand pairs for which property (S) has been proved includes those with G compact (compact pairs) [ 3 ], various families with \(G=K\ltimes H\) and H nilpotent (nilpotent pairs) [ 1 , 2 , 8 , 9 , 10 ], and those with \(G=K\ltimes H\) and K abelian [ 3 , Thm. 8.1]. No example in which condition (S) fails has been found so far.
An interesting class of Gelfand pairs for which Schwartz correspondence has not been established yet consists of the strong Gelfand pairs .
Denoting by \(\textrm{Int}(K)\) the group of inner automorphisms of G induced by elements of K and calling K -central a function on G that is \(\textrm{Int}(K)\) -invariant, the pair ( G , K ) is called a strong Gelfand pair if the algebra \(L^1(G)^{\textrm{Int}(K)}\) of K -central integrable functions is commutative. The term “strong” is then justified by the obvious fact that bi- K -invariant functions are K -central.
It is easy to verify that \(L^1(G)^{\textrm{Int}(K)}\approx L^1\big (K\backslash (K\ltimes _{\textrm{Int}} G)/K\big )\) , so that ( G , K ) is strong Gelfand if and only if \((K\ltimes _{\textrm{Int}} G,K)\) is Gelfand.
According to a general structure of Gelfand pairs due to Vinberg [ 23 , Thm. 13.3.20], Gelfand pairs ( G , K ) must have \(G=L\ltimes H\) , with H nilpotent of step \(\le 2\) and \(L\supseteq K\) orbit-equivalent to K . The case of a strong Gelfand pairs corresponds to \(L= K\ltimes _{\textrm{Int}} K\) .
A careful analysis of the classification in [ 24 ] shows that the non-compact strong Gelfand pairs ( G , K ) with polynomial growth have \(G=K\ltimes H\) and one of the following forms:
\(K=SO_n\) and \(H={\mathbb {R}}^n\) ,
\(K=U_n\) and \(H={\mathbb {C}}^n\) or the Heisenberg group \(H_n\) ,
direct products of the above.
Objects and notions given above for general Gelfand pairs can be reformulated in the following terms for a strong Gelfand pair ( G , K ), cf. [ 3 , Sect. 2.1]:
\({\mathbb {D}}(G)^{\textrm{Int}(K)}\) is the algebra of K -central differential operators on G ,
the spherical functions are the K -central eigenfunction of all operators in \({\mathbb {D}}(G)^{\textrm{Int}(K)}\) , normalized so that they take value 1 at the identity.
Then the Gelfand spectrum \(\Sigma \) consists of the bounded spherical functions and, given a finite generating system \({\mathcal {D}}\) of \({\mathbb {D}}(G)^{\textrm{Int}(K)}\) , the embedded copy \(\Sigma _{\mathcal {D}}\) of \(\Sigma \) is defined as the set of \((\textrm{dim}{\mathcal {D}})\) -tuples of eigenvalues like in the general case, and the spherical transform is defined as in ( 1.2 ). The formulation of Schwartz correspondence for strong Gelfand pairs with polynomial growth is the same as in (S), only with \({\mathcal {S}}(K\backslash G/K)\) replaced by \({\mathcal {S}}(G)^{\textrm{Int}(K)}\) .
The cases in which K is abelian are already covered by the positive results in [ 3 ]. The authors have recently proved property (S) for the strong pair \(\big (M_2({\mathbb {C}}),U_2\big )\) , where \(M_2({\mathbb {C}})=U_2\ltimes {\mathbb {C}}^2\) is the complex motion group in two dimensions [ 4 ].
In this paper we consider the strong pairs \(\big (M_n({\mathbb {R}}),SO_n\big )\) with \(n=3,4\) and prove the following.
Theorem 1.1
The strong Gelfand pairs \(\big (M_n({\mathbb {R}}),SO_n\big )\) , with \(n=3,4\) , satisfy property (S), i.e., the spherical transform maps \({\mathcal {S}}(M_n({\mathbb {R}}))^{\textrm{Int}(SO_n)}\) isomorphically onto \({\mathcal {S}}(\Sigma _{\mathcal {D}})\) .
One important tool in the analysis of K -central functions for general strong Gelfand pairs is decomposition into K -types.
Given \(\tau \in {\widehat{K}}\) , let \(f_\tau \) be the K -type component of \(f\in L^1(G)^{\textrm{Int}(K)} \) defined by
where \(d_\tau \) and \(\chi _\tau \) are character and dimension of \(\tau \) , respectively. We say that f has K -type \(\tau \) if \(f_\tau =f\) . The algebra \(L^1(G)^{\textrm{Int}(K)}\) decomposes as the direct sum of the subalgebras \(L^1(G)_\tau ^{\textrm{Int}(K)}\) of K -central functions of K -type \(\tau \) . Morever, for \(\tau \ne \tau '\) ,
and, denoting by \(\tau _0\) the trivial representation, \(L^1(G)_{\tau _0}^{\textrm{Int}(K)}=L^1(K\backslash G/K)\) .
It follows that ( G , K ) is a strong Gelfand pair if and only \((G,K,\tau )\) is a commutative triple (i.e., \(L^1(G)_\tau ^{\textrm{Int}(K)}\) is commutative) for every \(\tau \in {\widehat{K}}\) [ 20 ]. If this is the case, then \(\Sigma \) is the disjoint union of the spectra \(\Sigma ^\tau \) of \(L^1(G)_\tau ^{\textrm{Int}(K)}\) , consisting of the bounded spherical function that are of type \(\tau \) .
We can then extend the notion of Schwartz correspondence to the commutative triple \((G,K,\tau )\) as follows.
The \(\tau \) -spherical transform maps \({\mathcal {S}}(G)^{\textrm{Int}(K)}_\tau \) isomorphically onto the space \({\mathcal {S}}(\Sigma ^\tau _{\mathcal {D}})\) , where \(\Sigma ^\tau _{\mathcal {D}}\) is the Gelfand spectrum of \(L^1(G)_\tau ^{\textrm{Int}(K)}\) .
It is quite clear that, if the strong Gelfand pair ( G , K ) satisfies property (S), then property ( \(\textrm{S}_\tau \) ) is satisfied for every \(\tau \in {\widehat{K}}\) . Conversely, if we assume that property ( \(\textrm{S}_\tau \) ) has been proved for every \(\tau \) , it is still necessary to take into account the dependence on \(\tau \) of the Schwartz norm estimates involved. The following reduction principle of property (S) to single K -types has been used in [ 4 ] for the strong Gelfand pair \(\big (M_2({\mathbb {C}}),U_2\big )\) and will be used here to prove Theorem 1.1 .
Theorem 1.2
([ 3 , Prop. 5.2 and Thm. 7.1]) Property (S) holds for a strong Gelfand pair ( G , K ) of polynomial growth if and only if the following condition is satisfied:
given \(f\in {\mathcal {S}}(G)^{\textrm{Int}(K)}\) and \(N\in {\mathbb {N}}\) , for each K -type component \(f_\tau \) of f , \(\tau \in {\widehat{K}}\) , \({\mathcal {G}}f_\tau \) admits a Schwartz extension \(u_{\tau ,N}\) such that \(\Vert u_{\tau ,N}\Vert _{(N)}\) is rapidly decaying in \(\tau \) .
In the two cases considered here, \(n=3,4\) , the copy \(\Sigma _{\mathcal {D}}\) of the spectrum is embedded in \({\mathbb {R}}^n\) and its subsets \(\Sigma ^\tau _{\mathcal {D}}\) lie in distinct parallel 2-dimensional affine subspaces, so that, as long as we treat each \(\tau \) separately, \(\Sigma ^\tau _{\mathcal {D}}\) can be regarded as being embedded in \({\mathbb {R}}^2\) and \({\mathcal {G}}f_\tau \) as a function of two variables only. In this picture \(\Sigma ^\tau _{\mathcal {D}}\) is the union of finitely many half-parabolas if \(n=3\) , and of finitely many half-lines if \(n=4\) , all exiting from the origin. The number of half-parabolas, or of half-lines, increases with the dimension of \(\tau \) .
In order to obtain property (S’) we prove the following two facts:
for general \(f\in {\mathcal {S}}\big (M_n({\mathbb {R}})\big )^{\textrm{Int}(SO_n)}\) and any \(\tau \in \widehat{SO_n}\) , it is possible to determine a formal two-variable power series \(s_\tau (\xi _1,\xi _2)=\sum _{p,q}\frac{a^\tau _{p,q}}{p!q!}\xi _1^p\xi _2^q\) with the property that, for any \(N\in {\mathbb {N}}\) , there are functions \(h_{\tau ,N}\in {\mathcal {S}}({\mathbb {R}}^2)\) with rapidly decaying N -th Schwartz norm, Taylor expansion at 0 equal to \(s_\tau \) , and \({\mathcal {G}}f_\tau -h_{\tau ,N} \) vanishing of infinite order at 0 (Propositions 6.2 and 6.4 );
an explicit extension formula for \({\mathcal {G}}f_\tau \) exists, with the decay in \(\tau \) prescribed in (S’), under the assumption that \({\mathcal {G}}f_\tau \) vanishes of infinite order at \(0\in \Sigma _{\mathcal {D}}^\tau \) (Proposition 6.5 ).
Once (i) and (ii) are verified, an application of [ 16 , Prop. 4.2.1] gives the desired extensions \(u_{\tau ,N}\) of \({\mathcal {G}}f_\tau \) , satisfying condition (S’) (Proposition 6.6 ). Following this approach, the major obstacle consists in proving the existence of the formal power series \(s_\tau \) with the properties in (i), because the analysis of \({\mathcal {G}}f_\tau \) near 0 only gives, at any degree, a certain number of linear relations among the unknown coefficients \(a^\tau _{p,q}\) . These relations lead to infinitely many, overdetermined in general, linear systems in the \(a^\tau _{p,q}\) and the crucial problem is their solvability, a property apparently impossible to obtain by plain linear algebra.
Once solvability is proved the decay estimates in (i) can be proved in a relatively easy way. In order to bypass this problem, we introduce an analytic argument to directly obtain \((\textrm{S}_\tau )\) for every \(\tau \) , though not necessarily with the decay estimates required in (S’).
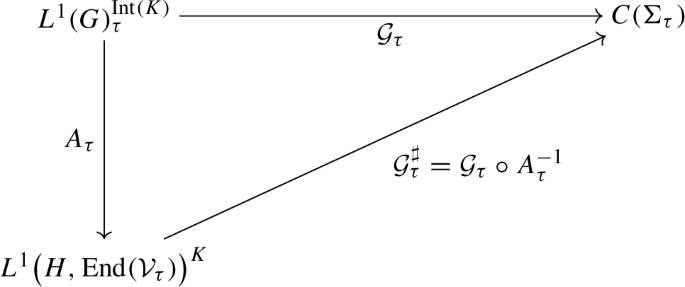
This argument exploits the identification, via an isomorphism \(A_\tau \) , of \(L^1\big (M_n({\mathbb {R}})\big )_\tau ^{\textrm{Int}(SO_n)}\) with the algebra \(L^1\big ({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau )\big )^{SO_n}\) of \(\textrm{End}({\mathcal {V}}_\tau )\) -valued, \(SO_n\) -equivariant, integrable functions on \({\mathbb {R}}^n\) , \({\mathcal {V}}_\tau \) being a representation space of \(\tau \) . The map \(A_\tau \) also gives a correspondence between the two sets of spherical functions and induces a homomorphisms from \({\mathbb {D}}\big (\! M_n({\mathbb {R}})\big )^{\textrm{Int}({SO}_n)\!}\) onto \(\big ({\mathbb {D}}({\mathbb {R}}^n)\otimes \textrm{End}({\mathcal {V}}_\tau )\big )^{{SO}_n\!}\) , the algebra of \(\textrm{End}({\mathcal {V}}_\tau )\) -valued, \({SO}_n\) -equivariant differential operators on \({\mathbb {R}}^n\) .
For both \(n=3\) and \(n=4\) , this last algebra admits a single generator \({\textbf{D}}_\tau \) as a \({\mathbb {D}}({\mathbb {R}}^n)^{{SO}_n}\) -module. For \(F\in {\mathcal {S}}\big ({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau )\big )^{SO_n}\) it is then possible to obtain the representation formula (Proposition 5.1 )
with m depending on \(\tau \) and the \(g_j\) radial, scalar-valued, Schwartz functions on \({\mathbb {R}}^n\) . This reduces the problem to the existence of a Schwartz extension for the Hankel transform of each \(g_j\) , and this is a trivial consequence of the Whitney representation theorem for even functions on \({\mathbb {R}}\) .
Though the general plan described above corresponds to that already used in [ 4 ], the detailed treatment presents here some new complications. In principle, the same strategy of proof of Schwartz correspondence can be extended to real and complex motion pairs in higher dimensions, but the algebraic problems arising in Sects. 4 and 5 become much more delicate.
Our paper is organized as follows. In Sect. 2 we recall some preliminary facts about strong Gelfand pairs of polynomial growth and describe the decomposition into K -types. Moreover, specializing to the case where \(G=K\ltimes _\delta H\) , we describe the isomorphism \(A_\tau \) between \({\mathcal {S}}\big (G\big )^{\textrm{Int}(K)}_\tau \) and \({\mathcal {S}}\big (H,\textrm{End}({\mathcal {V}}_\tau )\big )^{K}\) . In Sect. 3 we fix \(\tau \in \widehat{{SO}_n}\) and, for any n , we recall from [ 20 ] some general facts about the algebra \(\big ({\mathbb {D}}({\mathbb {R}}^n)\otimes \textrm{End}({\mathcal {V}}_\tau )\big )^{{SO}_n}\) and the Gelfand spectrum of \(L^1\big ({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau )\big )^{{SO}_n}\) . Starting from Sect. 4 , we limit ourselves to the cases \(n=3,4\) . First we choose a priviliged generating system of \(\big ({\mathbb {D}}({\mathbb {R}}^n)\otimes \textrm{End}({\mathcal {V}}_\tau )\big )^{{SO}_n}\) and spot the main differences between the cases \(n=3\) and \(n=4\) . Then we fix notation in order to treat the two cases in a unified way as far as possible and we determine the Gelfand spectrum \(\Sigma ^\tau _{\mathcal {D}}\) . In Sect. 5 we apply the results of the previous section to obtain the decomposition formula ( 1.5 ) and we show that property ( \(\textrm{S}_\tau \) ) holds for each \(\tau \in \widehat{{SO}_n}\) . In Sect. 6 we derive, for fixed \(\tau \) , the linear systems whose solutions allow us to obtain the infinite order local approximations \(\{h_{\tau , N}\}_N\) of \({\mathcal {G}}_\tau f_\tau \) with rapid decay, according to (i) above. At this stage, dealing with the linear systems, we have to introduce new technical arguments with respect to [ 4 ]. Finally we sum up all our results proving that the Schwartz correspondence holds for \(\big (M_n({\mathbb {R}}),SO_n\big )\) with \(n=3,4\) .
2 Spherical transforms for strong Gelfand pairs
In this section we fix notation, recall basic facts and prove some statements in the general context of a strong Gelfand pair ( G , K ) of polynomial growth. For details and unproven statements, we refer to [ 3 , 20 ].
The main result in the first subsection is the polynomial growth of the norms of \({\mathcal {G}}_\tau ^{-1}\) , the inverse of the \(\tau \) -spherical transform on \({\mathcal {S}}(G)^{\textrm{Int}(K)}_\tau \) .
In the second subsection we specialize to the case where \(G=K\ltimes _\delta H\) . In the analysis of functions of a given K -type, a matrix realization is often used, see [ 20 ] and the references therein. Specifically, in Proposition 2.4 we prove that \({\mathcal {S}}(G)^{\textrm{Int}(K)}_\tau \) is algebraically and topologically isomorphic to \({\mathcal {S}}\big (H,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) , the space of Schwartz \(\textrm{End}({\mathcal {V}}_\tau )\) -valued equivariant functions on H , i.e. satisfying ( 2.1 ).
2.1 The \(\tau \) -spherical transform and its inverse.
Let ( G , K ) be a strong Gelfand pair. We need notational conventions in order to distinguish among the different Gelfand structures that intervene.
The plain symbols \(\Sigma \) and \({\mathcal {G}}\) denote, respectively, Gelfand spectrum and spherical transform of ( G , K ) as strong pair, i.e., the set of multiplicative linear functionals of the full algebra \(L^1(G)^{\textrm{Int}(K)}\) endowed with the weak \(^*\) topology. The symbols \(\Sigma ^\tau \) and \({\mathcal {G}}_\tau \) denote, respectively, Gelfand spectrum and spherical transform (or \(\tau \) - spherical transform ) of the commutative triple \((G,K,\tau )\) , i.e., of the algebra \(L^1(G)^{\textrm{Int}(K)}_\tau \) . As usual, each multiplicative linear functional is realized by integration with a bounded spherical function. It is a fact [ 20 ] that every bounded spherical function is of K -type \(\tau \) for some, hence unique, \(\tau \in {\widehat{K}}\) . Hence \(\Sigma \) is the disjoint union of the spectra \(\Sigma ^\tau \) , consisting of the bounded spherical functions of type \(\tau \) (or \(\tau \) - spherical functions ). In particular, \(\Sigma ^{\tau _0}\) and \({\mathcal {G}}_{\tau _0}\) are Gelfand spectrum and spherical transform of the (ordinary) Gelfand pair ( G , K ). By ( 1.4 ), the spherical transform \({\mathcal {G}}f\) of \(f\in L^1(G)^{\textrm{Int}(K)}\) restricts to \(\Sigma ^\tau \) as the \(\tau \) -spherical transform \({\mathcal {G}}_\tau f_\tau \) of its \(\tau \) -component.
If G is connected and denoting by \({\mathbb {D}}(G)^{\mathrm{{Int}}(K)}\) the algebra of left-invariant differential operators on G that are also \(\textrm{Int}(K)\) -invariant, the bounded spherical functions are the elements of \(C^\infty (G)^{\textrm{Int}(K)}\) that are eigenfunctions of all elements of \({\mathbb {D}}(G)^{\mathrm{{Int}}(K)}\) , normalized to attain value 1 at the identity.
By the general facts about Gelfand pairs mentioned in the introduction, it follows that, if G has also polynomial growth, the choice of a finite system \({\mathcal {D}}=\{D_1,\dots ,D_\ell \}\) of symmetric generators of \({\mathbb {D}}(G)^{\mathrm{{Int}}(K)}\) determines a homeomorphism \(\iota _{\mathcal {D}}\) of \(\Sigma \) with a closed subset \(\Sigma _{\mathcal {D}}\) of \({\mathbb {R}}^{\ell }\) .
We shall always assume that G is connected with polynomial growth.
It is convenient to choose \({\mathcal {D}}\) of the form \({\mathcal {D}}={\mathcal {D}}'\cup {\mathcal {D}}''\) , where \({\mathcal {D}}'=\{D_1,\dots ,D_{\ell '}\}\) generates the center of \({\mathbb {D}}(K)\) . Then the homeomorphism \(\iota _{\mathcal {D}}=(\iota _{\mathcal {D}}',\iota _{\mathcal {D}}'')\) maps \(\varphi \in \Sigma \) to a point
When \(\varphi \) is \(\tau \) -spherical, the coordinates of \(\xi '_\tau =\iota '_{\mathcal {D}}(\varphi )\) are the eigenvalues of \(\overline{\chi _\tau }\) under \(\{D_1,\dots ,D_{\ell '}\}\) and
is homeomorphic to \(\Sigma ^\tau \) . Note also that rapid decay in \(\tau \) can be measured in terms of powers of \(|\xi '_\tau |\) (see [ 3 , formula (7.2)]).
With a language abuse the spherical transform of a function in \({\mathcal {S}}(G)^{\textrm{Int}(K)}\) will be considered as a function on \(\Sigma _{\mathcal {D}}\subset {\mathbb {R}}^\ell \) , and the \(\tau \) -spherical transform of a function in \({\mathcal {S}}(G)^{\textrm{Int}(K)}_\tau \) will be considered as a function on \(\Sigma ^\tau _{\mathcal {D}}\subset {\mathbb {R}}^{\ell ''}\) . In formulae, for every \(f\in {\mathcal {S}}(G)^{\textrm{Int}(K)}\) ,
In particular, when f is of type \(\tau \) ,
For a fixed compact, symmetric neighborhood U of the identity e of G , define
For our convenience we will use the following Schwartz norms. For \(N\in {\mathbb {N}}\) ,
where for every multiindex \(\alpha =(\alpha _1,\dots ,\alpha _\ell )\)
When C is a closed set of \({\mathbb {R}}^\ell \) , \({\mathcal {S}}(C)\) denotes the space of restrictions to C of Schwartz functions on \({\mathbb {R}}^\ell \) , that is
endowed with the quotient topology, induced by the norms i.e.
By the Plancherel-Godement Theorem [ 23 , p. 193] the spherical transform \({\mathcal {G}}\) is a unitary operator from \(L^2(G)^{\textrm{Int}(K)}\) onto \(L^2(\Sigma _{\mathcal {D}}, \beta )\) , where \(\beta \) is the Plancherel measure on \(\Sigma _{\mathcal {D}}\) . Since the symmetric operators \(D_j\) are essentially self-adjoint [ 18 ], the set \(\Sigma _{\mathcal {D}}\subset {\mathbb {R}}^\ell \) is their joint \(L^2(G)^{\textrm{Int}(K)}\) -spectrum (see [ 3 , Proposition 4.4]). In spectral analytic terms, \({\mathcal {G}}^{-1}\psi \) is the convolution kernel of \(\psi (D_1,\dots ,D_\ell )\) .
We can then rephrase a multiplier theorem by A. Martini [ 16 , Prop. 4.2.1] in the following way.
Proposition 2.1
The map \({\mathcal {G}}^{-1}\) is continuous from \( {\mathcal {S}}(\Sigma _{\mathcal {D}})\) in \({\mathcal {S}}(G)^{\textrm{Int}(K)}\) , i.e., for every \(N\in {\mathbb {N}}\) there exist \(M=M(N)\) and \(C_N\) such that
The use of this proposition is twofold. First, Proposition 2.1 , combined with the open mapping theorem for Fréchet spaces, allows us to disregard continuity of \({\mathcal {G}}\) . In other words, in order to prove that property (S) holds for the strong Gelfand pair ( G , K ), we only need to prove that \({\mathcal {G}}^{-1}\) is surjective, i.e., for every \(f\in {\mathcal {S}}(G)^{\text {Int}(K)}\) , the spherical transform \({\mathcal {G}}f\) extends to a Schwartz function on \({\mathbb {R}}^\ell \) . This will be proved by reduction to K –types according to the criterion in Theorem 1.2 .
The second application of Proposition 2.1 consists in establishing an analogous result for a fixed K –type \(\tau \) . This will be used in the proof of our main result (Proposition 6.6 ) as a tool in the construction of the extension with norms of rapid decay in \(\tau \) as required in Theorem 1.2 .
Corollary 2.2
Let \(\tau \) be in \({\widehat{K}}\) . Every \(v\in {\mathcal {S}}(\Sigma ^\tau _{\mathcal {D}})\) is the spherical transform of a unique function \({\mathcal {G}}^{-1}_\tau v\in {\mathcal {S}}(G)_\tau ^{\textrm{Int}(K)}\) . Moreover for every \(N\in {\mathbb {N}}\) there exist \(M=M(N)\) , \(M'=M'(N)\) and \(C_N\) such that
The starting point is the existence, for each \(\tau \in {\widehat{K}}\) , of a Schwartz function \(u_\tau \in {\mathcal {S}}({\mathbb {R}}^{\ell '})\) such that \(u_\tau (\xi '_\tau )=1\) , \(u_\tau (\xi '_\sigma )=0\) if \(\sigma \in \widehat{K}\) , \(\sigma \ne \tau \) and for every N there exist \( N'=N'(N)\) and \(C_N\) such that
This fact has been proved in [ 3 , Lemma 7.2].
Suppose now we are given \(v\in {\mathcal {S}}(\Sigma ^\tau _{\mathcal {D}})\) and let \(v_*\in {\mathcal {S}}({\mathbb {R}}^{\ell ''})\) be an extension of it. Define a Schwartz function \( u_*\) on \({\mathcal {S}}({\mathbb {R}}^\ell )\) by
and denote by u its restriction to \(\Sigma _{\mathcal {D}}\) . By Proposition 2.1 the function \(f={\mathcal {G}}^{-1} u\) belongs to \({\mathcal {S}}(G)^{\textrm{Int}(K)}\) and for every \(N\in {\mathbb {N}}\) there exist \(M=M(N)\) , \(M'=M'(N)\) and \(C_N\) such that
which implies that f is of type \(\tau \) and
Uniqueness of v is obvious, because \(L^1(G)^{\textrm{Int}(K)}_\tau \) is semisimple. \(\square \)
2.2 \(\textrm{End}({\mathcal {V}}_\tau )\) -valued Schwartz functions
For the purposes of this paper, we will introduce \(\textrm{End}({\mathcal {V}}_\tau )\) -valued functions only in the case of a strong Gelfand pair ( G , K ) with \(G=K\ltimes _\delta H\) and K is compact and acting on the nilpotent group H by \(\delta \) .
We denote by \({\mathcal {V}}_\tau \) the representation space of \(\tau \) , by \(d_\tau \) its dimension and by \(\textrm{End}({\mathcal {V}}_\tau )\) the algebra of linear endomorphisms of \({\mathcal {V}}_\tau \) . The space of integrable \(\textrm{End}({\mathcal {V}}_\tau )\) -valued functions on H is an algebra with convolution defined by
and norm \(\Vert F\Vert _1=\int _H\Vert F(h)\Vert _{\textrm{op}}\, dh\) .
We say that an \(\textrm{End}({\mathcal {V}}_\tau )\) -valued function F on H is K -equivariant if it satisfies
and denote by \(L^1\big (H,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) , and similarly for other function spaces, the subspace of integrable K -equivariant functions.
The two maps
establish a one-to-one correspondence between K -central functions f on G of K -type \(\tau \) and K -equivariant \(\textrm{End}({\mathcal {V}}_\tau )\) -valued functions on H .
In particular, \(A_{\tau }\) is an isomorphism of algebras from \(L^1(G)^{\textrm{Int}(K)}_{\tau }\) onto \(L^1\big (H,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) and \(\sqrt{d_\tau }A_{\tau }\) is unitary from \(L^2(G)^{\textrm{Int}(K)}_{\tau }\) onto \(L^2\big (H,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) , where
and \(\Vert \cdot \Vert _{\textrm{HS}}\) is the Hilbert-Schmidt norm.
Via the map \(A_\tau \) , we can then redefine the ingredients of the spherical analysis of K -central functions of type \(\tau \) on G in terms of the above \(\textrm{End}({\mathcal {V}}_\tau )\) –valued model.
This will be explained in detail in the next section in the case of the euclidean motion group, where we explicitly determine the \(\textrm{End}({\mathcal {V}}_\tau )\) –valued spherical functions, their eigenvalues and we deduce, via \(A_\tau \) , the \(\tau \) -spherical ones. We denote by \(\big ({\mathbb {D}}(H)\otimes \textrm{End}({\mathcal {V}}_\tau )\big )^K\) the algebra of “ \(\textrm{End}({\mathcal {V}}_\tau )\) –valued” differential operators on H which commute with translations and with the action of K on smooth \(\textrm{End}({\mathcal {V}}_\tau )\) –valued functions F given by
Conjugation by \(A_{\tau }\) is a homomorphism of \({\mathbb {D}}(G)^{\textrm{Int}(K)}\) onto \(\big ({\mathbb {D}}(H)\otimes \textrm{End}({\mathcal {V}}_\tau )\big )^{K}\) and its kernel consists of the operators which vanish on functions of K -type \(\tau \) .
The following lemma allows us to disregard the operators in \({\mathcal {D}}'\) , the center of \({\mathbb {D}}(K)\) , in the evaluation of the Schwartz norms of functions in \({\mathcal {S}}\big (H,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) .
Let \(\tau \in {\widehat{K}}\) and \(D_j\) be in \({\mathcal {D}}'\) . Then \(A_\tau D_j A_\tau ^{-1}\) is the scalar multiplication operator by \(\xi _j\) so that for every F in \(C^\infty \cap L^2\big (H,\textrm{End}({\mathcal {V}}_\tau )\big )^K\)
Let \(\xi '_\tau =(\xi _1,\ldots ,\xi _{\ell '})\) , where \(\xi _j\) is the eigenvalue of \({{\overline{\chi }}}_\tau \) under \(D_j\in {\mathcal {D}}'\) . Given F in \(C^\infty \cap L^2\big (H,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) , the function \(f =A_\tau ^{-1}F\) is in \(C^\infty \cap L^2(G)^{\textrm{Int}(K)}_\tau \) , so that by ( 1.3 )
Therefore applying the isomorphism \(A_\tau \) we obtain
and the thesis follows. \(\square \)
The following proposition establishes that \(A_\tau \) is a topological isomorphisms from \({\mathcal {S}}(G)^{\textrm{Int}(K)}_\tau \) onto \({\mathcal {S}}\big (H,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) .
As N -order Schwartz norm of a function F in \({\mathcal {S}}\big (H,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) we take
where for every multiindex \(\beta =(\beta _1,\dots ,\beta _{\ell ''})\)
Proposition 2.4
Let \(\tau \in {\widehat{K}}\) and N in \({\mathbb {N}}\) . The following estimates hold
Let \(f\in {\mathcal {S}}(G)^{\textrm{Int}(K)}_{\tau }\) . Since \(\sqrt{d_\tau }A_\tau \) is an isometry on \(L^2\) -spaces, we have
where \((D'')^\beta =(D_{\ell '+1})^{\beta _{1}}\cdots (D_{\ell })^{\beta _{\ell ''}}\) . Conversely, using Lemma 2.3 with \(F=A_\tau f\)
\(\square \)
Corollary 2.5
The map \(A_\tau \) is a topological isomorphism from \({\mathcal {S}}(G)^{\textrm{Int}(K)}_\tau \!\) onto \({\mathcal {S}}\big (H,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) .
3 \(\tau \) -spherical analysis on the euclidean motion group \({SO}_n\ltimes {\mathbb {R}}^n\)
In this section we introduce the euclidean motion group \(G={SO}_n\ltimes _\delta {\mathbb {R}}^n\) for general n . We recall some basic facts about the algebra \(\big ({\mathbb {D}}({\mathbb {R}}^n)\otimes \textrm{End}({\mathcal {V}}_\tau )\big )^{K}\) and the Gelfand spectrum \(\Sigma ^\tau \) of \(L^1\big ({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau )\big )^{K}\) .
3.1 The euclidean motion group
The euclidean motion group is the semidirect product \(G={SO}_n\ltimes _\delta {\mathbb {R}}^n\) where the action \(\delta \) of \(K={SO}_n\) on \({\mathbb {R}}^n\) is the natural one, i.e., \(\delta (k)y=k\, y\) . We write its elements as pairs \((k,y)\in {SO}_n\times {\mathbb {R}}^n\) with product law
so that the action of K on G by inner automorphisms is given by
It is well known that the algebra \(L^1(G)^{\textrm{Int}(K)}\) is commutative, i.e., the pair ( G , K ) is a strong Gelfand pair [ 20 , 22 , 24 ].
3.2 Invariant differential operators
Differential operators in \({\mathbb {D}}(G)^{\mathrm{{Int}}(K)}\) are obtained from \(\textrm{Ad}(K)\) –invariant polynomials on the Lie algebra \({\mathfrak {g}}\) of G via the symmetrization procedure described in [ 20 , formula (2.4)].
Indeed, let p be in \({\mathcal {P}}({\mathfrak {g}})^{\textrm{Ad}(K)}\) and note that \({\mathfrak {g}}\) can be identified with \({\mathfrak {k}}\oplus {\mathbb {R}}^n\) , where \({\mathfrak {k}}=\mathfrak {so}_n\) , so that p satisfies
Then, using the symmetrization operator \(\lambda \) on the universal enveloping algebra \({\mathfrak {U}}({\mathfrak {k}})\) [ 21 , p. 180] and Fourier transform in y , we construct the corresponding operator \(D_p\in {\mathbb {D}}(G)^{\mathrm{{Int}}(K)}\) . Explicitly, for the choice of an orthonormal basis \(\{X_1,\ldots ,X_{n(n-1)/2}\}\) of \(\mathfrak {so}_n\) we write \(X=\sum _\ell x_\ell \, X_\ell \) and if
The coefficient i in both factors has been introduced in order to map real polynomials into symmetric operators.
For the reader’s convenience we recall that
with \(m=n(n-1)/2\) , and that we choose the following normalization of the Fourier transform of an integrable function f on \({\mathbb {R}}^n\)
Explicit families of generating polynomials of \({\mathcal {P}}({\mathfrak {g}})^{\textrm{Ad}(K)}\) can be found in [FRY1, Thm. 7.5(1)]. It is convenient for us to choose a set of generators \(\{p_1, \dots p_{\ell '}, q_1,\ldots , q_{\ell ''}\}\) , where the polynomials \(p_j\) depend only on the variables in \({\mathfrak {k}}\) , the polynomial \(q_1=|y|^2\) depends only on the \({\mathbb {R}}^n\) variables and the polynomials \(q_j\) with \(j>1\) may depend on both groups of variables.
Calling \(D_{p_j}\) , \(D_{q_j}\) the symmetrizations of the above polynomials, the operator \(D_{q_1}\) is (minus) the laplacian on \({\mathbb {R}}^n\) , i.e.,
and the operators \(D_{p_j}\) form the set \({\mathcal {D}}'\) in Sect. 2 so that their eigenvalues on each spherical function depend only on its type.
3.3 K -type subalgebras and \(\textrm{End}({\mathcal {V}}_\tau )\) -valued spherical analysis
We now focus on the commutative triple \((G,K,\tau )\) with \(\tau \in {\widehat{K}}\) and understand the structure of \(\textrm{End}({\mathcal {V}}_\tau )\) –valued functions F on \({\mathbb {R}}^n\) satisfying the K -equivariance condition ( 2.1 ), where \(\delta (k)y=k\,y\) .
This condition implies that such a function F is uniquely determined by its values for \(y=r{o}\) where \({o}=(1,0,\dots ,0)\) and \(r\ge 0\) , and that \(F(r{o})\) commutes with \(\tau (k)\) for all k in the stabilizer \(K_{o}\) of \({o}\) , i.e., \(k=\begin{bmatrix}1&{}0\\ 0&{}k'\end{bmatrix}\) with \(k'\in {SO}_{n-1}\) .
Since \(({SO}_n,{SO}_{n-1})\) is also a strong Gelfand pair, the restriction of \(\tau \) to \(K_{o}\) decomposes without multiplicities,
where \({\mathcal {U}}_{\sigma _j}\) is the representation space of \(\sigma _j\) and the \(\sigma _j\) are mutually inequivalent. Then, by Schur’s lemma,
where \(P_{s,\tau }\) is the orthogonal projection of \({\mathcal {V}}_\tau \) onto \({\mathcal {U}}_{\sigma _s}\) , so that
where \(d_{\sigma _s}=\textrm{dim}\,{\mathcal {U}}_{\sigma _s}\) .
Spherical functions have been determined in [ 20 , Sect. 7, 11] and we recall them in the following proposition. The Fourier transform of \(\textrm{End}({\mathcal {V}}_\tau )\) -valued functions is defined componentwise.
Proposition 3.1
The Gelfand spectrum \(\Sigma ^\tau \) of \(L^1\big ({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau )\big )^{K}\) consists of the multiplicative functionals
where \(\Phi ^\tau _{\rho ,s}\) is the \(\textrm{End}({\mathcal {V}}_\tau )\) -valued spherical function
with \(d_\tau = \textrm{dim}\,{\mathcal {V}}_\tau \) and \(d_{\sigma _s}=\textrm{dim}\,{\mathcal {U}}_{\sigma _s}\) , \(s=0,\ldots ,{a_\tau }\) .
For the reader’s convenience we explicit here the link between the two formulas in the statement and we refer to [ 20 ] for the other details. By ( 2.1 ), we have
Via the map \(A_\tau \) we infer that the multiplicative functionals of \(L^1(G)^{\textrm{Int}(K)}_\tau \) are given by
where the functions
are the \(\tau \) -spherical functions for the Gelfand pair \((K\ltimes _{\textrm{Int}} G,K)\) . Constants are arranged in such a way that \(\Phi ^\tau _{\rho ,s}(0)\) is the identity operator and \(\varphi ^\tau _{\rho ,s}(e,0)=1\) .
3.4 Differential operators in \(\big ({\mathbb {D}}({\mathbb {R}}^n)\otimes \textrm{End}({\mathcal {V}}_\tau )\big )^{K}\)
Suppose that p is in \({\mathcal {P}}({\mathfrak {g}})^{\textrm{Ad}(K)}\) . In Sect. 3.2 we developed a rule that generates the differential operator \(D_p\) in \({\mathbb {D}}(G)^{\mathrm{{Int}}(K)}\) (see formulas ( 3.1 ) and ( 3.2 )).
We can then obtain the differential operator \(D_p^\tau \) in \(\big ({\mathbb {D}}({\mathbb {R}}^n)\otimes \textrm{End}({\mathcal {V}}_\tau )\big )^{K}\) simply conjugating by \(A_\tau \) .
The purpose of the following lemma is to relate conjugation by \(A_\tau \) to the symmetrization procedure, specializing [ 20 , Corollary 2.3] to our case.
Suppose that p is as in ( 3.1 ). Then for every F in \({\mathcal {S}}\big ({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau )\big )^K\)
Let \(f_\tau =A_\tau ^{-1}F\) . Then with \(m=n(n-1)/2\)
4 Equivariant polynomials and the Gelfand spectrum \(\Sigma ^\tau _{\mathcal {D}}\) when \(n=3,4\)
From now on we will consider the cases where \(n=3,4\) . In this section we will compute, for any fixed \(\tau \) in \({\hat{K}}\) , the eigenvalues \(\xi '_\tau \) . Next we will consider the representation \({{\tilde{\tau }}}\) on \(\textrm{End}({\mathcal {V}}_\tau )\) given by
and decompose \(\textrm{End}({\mathcal {V}}_\tau )\) into irreducible invariant subspaces. The lower dimensional nontrivial subspace contains an element which turns out to be important in our analysis, because it coincides with the Fourier transform of one of the generators \(D^\tau _q\) at the basepoint. We shall denote this element by \(B_\tau \) . The main result is Lemma 4.2 where we determine which polynomials in \(B_\tau \) lie in the various irreducible invariant subspaces, and Proposition 4.4 , where we determine the Gelfand spectrum \(\Sigma ^\tau _{\mathcal {D}}\) .
4.1 The case where \(n=3\)
We denote by \(\tau _\mu \) , with \(\mu \in (1/2){\mathbb {N}}\) the irreducible representation of \(SU_2\) of dimension \(2\mu +1\) . For \(\mu \in {\mathbb {N}}\) , \(\tau _\mu \) projects to a representation of \(SO_3\equiv SU_2/{\mathbb {Z}}_2\) and \(\widehat{SO_3}=\{\tau _\mu :\mu \in {\mathbb {N}}\}\) .
The restriction of \(\tau _\mu \) to \(K_{o}\equiv SO_2\) in ( 3.3 ) decomposes as
where \(\sigma _s\left( \begin{bmatrix}\cos t&{}-\sin t\\ \sin t&{}\cos t\end{bmatrix}\right) \) is the character \(e^{i(s-\mu )t}\) . So \({\mathcal {V}}_{\tau _\mu }={\mathcal {U}}_{\sigma _0}\oplus \cdots \oplus {\mathcal {U}}_{\sigma _{2\mu }}\) and the spaces \({\mathcal {U}}_{\sigma _s}\sim {\mathbb {C}}\) are all one dimensional.
We choose the basis of \({\mathfrak {s}}{\mathfrak {o}}_3\) formed by the vectors
and we identify
with \(x=(x_1,x_2,x_3)\in {\mathbb {R}}^3\) . The following family of invariant polynomials of \({\mathcal {P}}({\mathfrak {g}})^{\textrm{Ad}(K)}\) is well known
Then the symmetrization map of Sect. 3.2 produces \(D_{p_1}=-\sum _{j=1}^3X_j^2\) , a constant multiple of the Casimir operator on \(SO_3\) , and
According to Lemma 3.2 , we obtain the following generating system of \(\big ({\mathbb {D}}({\mathbb {R}}^3)\otimes \textrm{End}({\mathcal {V}}_\tau )\big )^{K}\)
Identifying \(\textrm{End}({\mathcal {V}}_{\tau _\mu })\) with \( {\mathcal {V}}'_{\tau _\mu }\otimes {\mathcal {V}}_{\tau _\mu }\) , the representation \({{\tilde{\tau }}}_\mu \) defined in ( 4.1 ) is equivalent to the tensor product \(\tau '_{\mu }\otimes \tau _{\mu }\) , where \(\tau '_{\mu }\sim \tau _{\mu }\) is the contragredient representation of \(\tau _{\mu }\) .
Therefore \({{\tilde{\tau }}}_\mu \) decomposes as
and accordingly
where \(\textrm{dim}\,{\mathcal {W}}^\ell _{\tau _\mu }=2\ell +1\) .
and consider the \({{\tilde{\tau }}}_{\mu }\) -invariant subspace \({\mathcal {W}}\) generated by \(d\tau _\mu (X_1)\) . Then
which is a 3-dimensional invariant subspace. So it must coincide with the component \({\mathcal {W}}_{\tau _\mu }^1\) in ( 4.2 ).
For every \(\ell =0,\ldots ,2\mu \) , let \({\mathcal {B}}^\ell _{\tau _\mu }\) be the subspace of \(K_{o}\) -invariant elements in \({\mathcal {W}}^\ell _{\tau _\mu }\) . Since the representation \({{\tilde{\tau }}}_{\mu }\) restricted to \({\mathcal {W}}^\ell _{\tau _\mu }\) is equivalent to \(\tau _{\ell }\) , it contains the null weight with multiplicity one, and so \({\mathcal {B}}^\ell _{\tau _\mu }\) is one-dimensional. In particular, \(B_{\tau _\mu }\) spans \({\mathcal {B}}^1_{\tau _\mu }\) .
4.2 The case where \(n=4\)
When \(n=4\) , it is convenient to use the identifications
with one copy of \(\textrm{Sp}_1=\{u\in {\mathbb {H}}:|u|=1\}\) acting by left multiplication and the other by right multiplication on \({\mathbb {H}}\) ,
According to the previous identifications, the unitary dual \(\widehat{SO_4}\) consists of the exterior tensor products \(\tau _{\nu ,\mu }=\tau _\nu \boxtimes \tau _\mu \) , with \(\nu ,\mu \in (1/2){\mathbb {N}}\) and \(\nu +\mu \in {\mathbb {N}}\) .
The Lie algebra \(\mathfrak {so}_4\) can be identified with \({\mathfrak {s}}{\mathfrak {u}}_2\times {\mathfrak {s}}{\mathfrak {u}}_2\cong \text {Im}\,{\mathbb {H}}\times \text {Im}\,{\mathbb {H}}\) . For \(\alpha , \beta \in \text {Im}\,{\mathbb {H}}\) we shall write \(X_{\alpha , \beta }\) for the corresponding element in \(\mathfrak {so}_4\) . Differentiating ( 4.4 ) we obtain
be the standard basis of \({\mathfrak {s}}{\mathfrak {u}}_2\) . Denote these elements by \(U_1,U_2,U_3\) if they belong to the first copy of \({\mathfrak {s}}{\mathfrak {u}}_2\) , and by \(V_1,V_2,V_3\) if they belong to the second. The adjoint action of \(SO_4\) on \(\mathfrak {so}_4\times {\mathbb {R}}^4\) is given by
and we choose the following family of generating polynomials of \({\mathcal {P}}({\mathfrak {g}})^{\textrm{Ad}(K)}\)
Then \(\lambda (p_i)=C_i\) , a constant multiple of Casimir operator on the i -th copy of \(SU_2\) , so
and the \(\textrm{End}({\mathcal {V}}_{\tau _{\nu ,\mu }})\) -valued differential operators are
One could work out an explicit formula for \({\textbf{D}}_{\tau _{\nu ,\mu }}\) , but for our purposes it will suffice to know that for \({o}=1\in {\mathbb {H}}\)
which follows immediately from Lemma 3.2 .
The stabilizer \(K_{o}\) of \({o}\) is \(\textrm{diag}(SU_2\times SU_2)/{\mathbb {Z}}_2\cong SO_3\) . Since \((\tau _\nu \boxtimes \tau _\mu )_{|_{\textrm{diag}(SU_2\times SU_2)}}=\tau _\nu \otimes \tau _\mu \) , the analogue of formula ( 3.3 ) becomes
Therefore for \(j=0,\ldots ,2(\mu \wedge \nu )(=2\min \{\mu ,\nu \})\) , we let \(\sigma _j\sim \tau _{\mu +\nu -j}\) and \({\mathcal {U}}_{\sigma _j}\) for its representation space.
Since every \({SU_2}\) -factor acts on the corresponding factor space, for the action on \(\textrm{End}({\mathcal {V}}_{\tau _{\nu ,\mu }})\) we have the decomposition
corresponding to
We remark that, restricting the representation to \(K_{o}\) , \({\mathcal {W}}^{j,k}_{\tau _{\nu ,\mu }}\) contains a fixed element if and only if \(j=k\) .
For every \(\ell =0,1,\ldots ,2(\mu \wedge \nu )\) , we denote by \({\mathcal {B}}^\ell _{\tau _{\nu ,\mu }}\) the subspace of \(K_{o}\) -fixed matrices in \({\mathcal {W}}^{\ell ,\ell }_{\tau _{\nu ,\mu }}\) . The subspace \({\mathcal {B}}^\ell _{\tau _{\nu ,\mu }}\) is one-dimensional and consists of operators which are constant multiples of the identity operator on each \({\mathcal {U}}_{\sigma _s}\) .
As noted in the previous subsection, \(d\tau _\nu (U_j)\) is in \({\mathcal {W}}_{\tau _\nu }^1\) . Therefore \(B_{\tau _{\nu ,\mu }}\) is the only nontrivial element in \({\mathcal {B}}^1_{\tau _{\nu ,\mu }}\) .
Since \(K_{o}\) –invariant elements act as constants on \({\mathcal {U}}_{\sigma _s}\) , we may define coefficients \(\beta _{s,{\tau _{\nu ,\mu }}}\) so that
\(\beta _{s,\tau _{\nu ,\mu }}=4(\mu -s)(\nu -s)-2s(s+1)\) .
In the polynomial model \({\mathcal {V}}_{\tau _\nu }\otimes {\mathcal {V}}_{\tau _\mu }={\mathcal {P}}^{2\nu ,2\mu }({\mathbb {C}}^2)\) , we obtain
where \({\mathcal {H}}^{\alpha ,\beta }\) denotes the space of harmonic polynomials of bidegree \((\alpha ,\beta )\) .
Then \(d\tau _\nu (U_j)\) and \(d\tau _\mu (V_j)\) act respectively on the holomorphic and the antiholomorphic variables. Therefore we shall more briefly write \(Z_j=d\tau _\nu (U_j)\) and \(\bar{Z}_j=d\tau _\mu (V_j)\) so that
According to the above notation
Consider the polynomial in \({\mathcal {U}}_{\sigma _s}\) given by
Explicit computations show that
4.3 Polynomials in \(B_\tau \)
In order to treat the cases \(n=3,4\) together as far as possible, it is convenient to use the following notation. We recall that
and for \(j=0,\ldots ,{a_\tau }\) we put
For every \(\ell =0,\ldots ,a_\tau \) , there is a monic polynomial \(q_{\tau }^\ell \) of degree \(\ell \) such that \({\mathcal {B}}^\ell _{\tau }\) consists of the scalar multiples of \(q_{\tau }^\ell (B_\tau )\) .
Moreover, for a polynomial p of degree at most \({a_\tau }\) , we have \(p(B_\tau )\in \sum _{j\le \ell }{\mathcal {W}}_{\tau }^j\) if and only if \({\textrm{deg}}(p) \le \ell \) .
Finally, when \(n=3\) , \(q_{\tau }^\ell \) is of the same parity as \(\ell \) .
We start giving the proof in the case where \(n=3\) , so \(\tau =\tau _\mu \) and \(B_\tau =B_{\tau _\mu }\) , given in ( 4.3 ).
We proceed by induction proving all statements together. They are trivial for \(\ell =0\) and have been proved in Sect. 4.1 for \(\ell =1\) .
Let \(\ell \ge 2\) and consider the polynomial \(t\mapsto p(t)=t\, q_\tau ^{\ell -1}(t)\) . Then p is of degree \(\ell \) and \(p(B_\tau )\) is a \(K_{o}\) –invariant element. By the inductive hypothesis, \(q_\tau ^{\ell -1}(B_\tau )\) is in \({\mathcal {W}}_{\tau _\mu }^{\ell -1}\) and \(B_\tau \) is in \({\mathcal {W}}_{\tau _\mu }^{1}\) ; moreover we have \(\tau _\mu '\otimes \tau _\mu |_{{\mathcal {W}}_{\tau _\mu }^{\ell -1}}\sim \tau _{\ell -1}\) and the decomposition
in irreducible summands with multiplicity one for \(\tau _{\ell }\) . Therefore \(p(B_\tau )\) is in \({\mathcal {W}}_{\tau _\mu }^\ell \oplus \cdots \oplus {\mathcal {W}}_{\tau _\mu }^0\) with a nontrivial component in \({\mathcal {W}}_{\tau _\mu }^\ell \) . We call \(q_{\tau }^\ell (B_\tau )\) this component. Hence \((p-q_{\tau }^\ell )(B_\tau )\) is in \(\sum _{j\in L} {\mathcal {W}}_{\tau _\mu }^j\) , which, by the inductive hypothesis, is a polynomial in \(B_\tau \) of degree at most \(\ell -1\) . Then \(q_{\tau }^\ell \) has degree \(\ell \) and its leading term is the same as p , so it is monic.
As for the parity statement, note that the inner product is proportional to the Hilbert–Schmidt one so that
when \(\ell +\ell '\) is odd.
In the case where \(n=4\) , the proof is almost identical to the previous one; the only difference lies in the fact that in the decomposition
in irreducible summands with multiplicity one for \(\tau _{\ell }\boxtimes \tau _{\ell }\) , \(K_{o}\) –invariant elements arise only when \(j=k\) . \(\square \)
4.4 Equivariant homogeneous polynomials
Denote by \(Q_\tau \) the K –equivariant polynomial arising from the symmetrization of the polynomial \(q_2\) and Lemma 3.2 . Explicity,
This polynomial is also completely determined by the following properties:
\(Q_\tau ({o})=B_\tau \) ;
\(Q_\tau \) is K -equivariant;
\(Q_\tau \) is of least degree.
Note that \(Q_\tau \) is homogeneous of degree \(\kappa \) where
Suppose now that \(P:{\mathbb {R}}^n\rightarrow \textrm{End}({\mathcal {V}}_\tau )\) is a K -equivariant polynomial. Then each homogeneous component of P is also equivariant and P can be uniquely decomposed as the sum of \({\mathcal {W}}_{\tau }^\ell \) -valued homogeneous polynomials.
Proposition 4.3
Suppose that there exists a nontrivial K –equivariant polynomial, homogeneous of degree d and \({\mathcal {W}}_{\tau }^\ell \) –valued. Then \(d\ge \ell \kappa \) and \(d-\ell \kappa \) is even.
Suppose that \(P:{\mathbb {R}}^n\rightarrow \textrm{End}({\mathcal {V}}_\tau )\) is a nontrivial K –equivariant polynomial homogeneous of degree d and \({\mathcal {W}}_{\tau }^\ell \) -valued. Since \(P({o})\) is in \({\mathcal {B}}_\tau ^\ell \) , by Lemma 4.2
for some constant c . Setting \(y'=y/|y|\) for \(y\ne 0\) ,
Since in the last equation there are no negative powers, we deduce that \(d\ge \ell \kappa \) . Finally, since P is a polynomial, \(d-\ell \kappa \) is even. \(\square \)
4.5 \(\textrm{End}({\mathcal {V}}_\tau )\) -valued spherical functions as derivatives of scalar spherical functions
For \(\rho \ge 0\) we denote by \(\varphi _\rho \) the spherical function of ( G , K ) as an ordinary Gelfand pair with eigenvalue \(\rho ^2\) relative to \(\Delta \) . In formulae,
and \(\sigma \) is the normalized surface measure of the unit sphere \(S^{n-1}\) in \({\mathbb {R}}^n\) .
Coherently with Lemma 4.1 , we call \(\beta _{s,\tau }\) the eigenvalue of \(B_\tau \) on the subspace \({\mathcal {U}}_{\sigma _s}\) . In formulae,
so that \(B_\tau =\sum _{s=0}^{{a_\tau }} \beta _{s,\tau }P_{s,\tau }\) . Note that, with respect to the notation in ( 3.4 ) \(\beta _{s,\tau }\) is a shorthand notation
Since \(\beta _{s,\tau }\ne \beta _{s',\tau }\) when \(s\ne s'\) , the orthogonal projection \(P_{s,\tau }\) of \({\mathcal {V}}_\tau \) onto \({\mathcal {U}}_{\sigma _s}\) can be written as a polynomial in \(B_\tau \) of degree \({a_\tau }\) . Indeed,
In the following proposition we write the \(\textrm{End}({\mathcal {V}}_\tau )\) -valued spherical functions as derivatives of scalar spherical functions and we observe that the distributional Fourier transform of \(\Phi ^\tau _{\rho ,s}\) is given in terms of the orthogonal projection \(P_{s,\tau }\) . As a consequence we easily compute the embedded spectrum \(\Sigma ^\tau _{\mathcal {D}}\) showing that it consists of half parabolas when \(n=3\) and rays through the origin when \(n=4\) .
Given an \(End ({\mathcal {V}}_\tau )\) -valued polynomial P , we denote by \(P(\partial )\) the differential operator defined by the rule
In particular note that
We recall that \(\kappa =1\) when \(n=3\) , and \(\kappa =2\) when \(n=4\) .
Proposition 4.4
The spectrum \(\Sigma ^\tau _{\mathcal {D}}\) is given by
Moreover, the \(\textrm{End}({\mathcal {V}}_\tau )\) -valued spherical function \(\Phi ^\tau _{\rho ,s}\) in ( 3.5 ) corresponds to the pair of eigenvalues \(\big (\rho ^2,\beta _{s,\tau }\,\rho ^\kappa \big )\) and satisfies
The case \(\rho =0\) is trivial. When \(\rho >0\) , by formula ( 3.5 ) we have
We now determine the embedded spectrum. From formula ( 3.5 ), it is easy to check that \(\Delta \Phi ^\tau _{\rho ,s}=\rho ^2\, \Phi ^\tau _{\rho ,s}\) . As for the second eigenvalue by ( 4.7 )
where \(C_{s,\tau }=\frac{d_\tau }{d_{\sigma _s}}\,\frac{(2\pi )^n}{|S^{n-1}|}\) . Hence by ( 3.4 ) and ( 4.6 ) we have
By homogeneity and equivariance we have
Since we regard the \(\tau \) -spherical transform as defined on the embedded spectrum, and according to Lemma 3.5 , we shall write
The next corollary shows that we can disregard part of the spectrum when dealing with even or odd functions in the case where \(n=3\) .
Corollary 4.5
In the case where \(n=3\) ,
so that if F is decomposed into its even part \(F_+\) and its odd part \(F_-\) , then
Note that when \(n=3\)
and since \(Q_{\tau }\) is homogeneous of degree \(\kappa =1\) ,
Moreover \(d_{\sigma _s}=1\) , so that
Finally, by a simple change of variables
and the desired formula follows remembering that, when \(\tau =\tau _\mu \) , \({a_\tau }=2\mu \) and \(\beta _{s,\tau }=-\mu +s\) , so \(\beta _{{a_\tau }-s,\tau }=-\beta _{s,\tau }\) . \(\square \)
5 Schwartz correspondence for \((G,K,\tau )\)
In this section we give our first argument to prove that \( {\mathcal {G}}_\tau ^\sharp \) maps \({\mathcal {S}}\big ({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) into \({\mathcal {S}}(\Sigma ^\tau _{\mathcal {D}})\) . The implied norm inequalities will be left implicit because their dependence on \(\tau \) is not sufficiently sharp for our purposes. Sharper estimates will be obtained in Sect. 6 .
The analysis of the Banach algebra \(L^1({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau ))^K\) developed in the previous section leads to the decomposition of \(\textrm{End}({\mathcal {V}}_\tau )\) –valued equivariant functions into a sum of derivatives of scalar valued functions.

Proposition 5.1
Let F be in \({\mathcal {S}}({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau ))^K\) . Then F can be expressed in a unique way as
with scalar valued functions \(g_i\in {\mathcal {S}}({\mathbb {R}}^n)^K\) .
Every F in \({\mathcal {S}}\big ({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) can be decomposed in a unique way as \(F=\sum _{\ell =0}^{{a_\tau }} F_\ell \) , where the component \(F_\ell \) is in \({\mathcal {S}}({\mathbb {R}}^n,{\mathcal {W}}_\tau ^\ell )^K\) . Therefore we start with a single \(F_\ell \) .
Since the Fourier transform commutes with rotations, \(\widehat{F_\ell }\) is in \({\mathcal {S}}({\mathbb {R}}^n,{\mathcal {W}}_\tau ^\ell )^K\) too, so that, by Lemma 4.2 , for every \(\rho \ne 0\) , \(\widehat{F_\ell }(\rho {o})\) is a constant multiple, \(f_\ell (\rho )\) say, of \(q_\tau ^\ell (B_\tau )\) .
Suppose that \(P_{\ell ,d}\) is the Taylor polynomial of \(\widehat{F_\ell }\) centred at the origin of order d . i.e.,
Then \(P_{\ell ,d}\) and all of its homogeneous components are K –equivariant and \({\mathcal {W}}_\tau ^\ell \) –valued. Therefore \( P_{\ell ,d}({o}) \) is a constant multiple of \(q_\tau ^\ell (B_\tau )\) . Using Proposition 4.3 we conclude that \(P_{\ell ,d}=0\) if \(d<\kappa \ell \) .
We can therefore write
Clearly the so-obtained function \(f_\ell \) is in \({\mathcal {S}}({\mathbb {R}})\) and of the same parity as \(\kappa \ell \) .
and by Hadamard’s division Lemma [ 17 ] there exists an even smooth function \({\tilde{f}}_\ell \) on \({\mathbb {R}}\) such that \(f_\ell (\rho )=\rho ^{\kappa \ell }\, {\tilde{f}}_\ell (\rho )\) and \(\tilde{f}_\ell (0)=c_\ell \) . With \(h_\ell ={\tilde{f}}_\ell (|\cdot |)\) , we conclude that when \(\eta =|\eta |\eta '\)
Therefore \(h_\ell \) is a uniquely determined scalar invariant Schwartz function on \({\mathbb {R}}^n\) and taking the inverse Fourier transform, for a scalar invariant Schwartz function \(\gamma _\ell \) on \({\mathbb {R}}^n\) ,
Since \(q^\ell _{\tau }\) is a polynomial of degree \(\ell \) , rearranging the terms in the sum
we obtain the desired decomposition. \(\square \)
Let F be in \({\mathcal {S}}\big ({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) . Then there exist \(\gamma _0,\ldots , \gamma _{a_\tau }\) in \( {\mathcal {S}}({\mathbb {R}})\) such that
Let F be in \({\mathcal {S}}\big ({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) and \(g_i\) be the K –invariant scalar functions we have associated to F in Proposition 5.1 . Then \(\widehat{g_i}\) is K –invariant, so that by Schwartz–Mather there exists a function \(\gamma _i \in {\mathcal {S}}({\mathbb {R}})\) such that
and by ( 4.5 )
Finally, by ( 4.8 ),
Given \(f\in {\mathcal {S}}(G)^{\textrm{Int}(K)}\) , via the map \(A_\tau \) , the following result gives the existence of an extension of \({\mathcal {G}}_\tau f_\tau \) for each \(\tau \in {\widehat{K}}\) .
Corollary 5.3
Let F be in \({\mathcal {S}}\big ({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) . Then
There exists \(u\in {\mathcal {S}}({\mathbb {R}}^2)\) such that \({u}_{ |_{\Sigma _{\mathcal {D}}^\tau }}={\mathcal {G}}^\sharp _\tau F\) .
The map \({\mathcal {G}}^\sharp _\tau \) is an isomorphism from \({\mathcal {S}}\big ({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) onto \({\mathcal {S}}(\Sigma _{\mathcal {D}}^\tau )\) .
The map \({\mathcal {G}}_\tau \) is an isomorphism from \({\mathcal {S}}(G)_{\tau }^{\textrm{Int}(K)}\) onto \({\mathcal {S}}(\Sigma _{\mathcal {D}}^\tau )\) .
Let \({\mathcal {C}}_\tau \) be the closed convex hull of \(\Sigma _{\mathcal {D}}^\tau \) and
Note that if \((\xi _1,\xi _2)\) is in \({\mathcal {C}}^1_\tau \) and \(\xi _1>1\) , then \(|\xi _2| \le R\, \xi _1\) for some \(R>0\) .
Let \(\eta \) be a smooth function on \({\mathbb {R}}^2\) which takes value 1 on \({\mathcal {C}}_\tau \) , vanishes outside \({\mathcal {C}}_\tau ^1\) and with bounded derivatives of any order. Let F be in \({\mathcal {S}}\big ({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) and let \(\gamma _0,\ldots , \gamma _n\) in \( {\mathcal {S}}({\mathbb {R}})\) be as in Lemma 5.2 such that
Define the Schwartz function g on \({\mathbb {R}}^2\) by
Then \({u}_{ |_{\Sigma _{\mathcal {D}}^\tau }}={\mathcal {G}}^\sharp _\tau F\) .
By Corollary 2.2 the map \({\mathcal {G}}_\tau ^{-1}\) is continuous and (ii) and (iii) follow by Corollary 2.5 . \(\square \)
6 Growth control for large \(\tau \) and conclusion
In this section we conclude the proof of Theorem 1.1 . As required in Theorem 1.2 , for each \(\tau \) and each order N , given f in \({\mathcal {S}}(G)^{\textrm{Int}(K)}\) , we produce an extension of \({\mathcal {G}}_\tau f_\tau \) with rapidly \(\tau \) -decaying norms up to order N . For this purpose we will follow steps (i) and (ii) in the Introduction.
We begin by observing that, as in the case of the euclidean Fourier transform, the derivatives of the spherical transform \({\mathcal {G}}_\tau f_\tau \) are controlled by Schwartz norms of \(f_\tau \) . This is shown in the next lemma, whose use is twofold. On the one hand it gives estimates of the coefficients of the formal power series \(s_\tau \) in (i) of the introduction (Proposition 6.2 ); on the other hand it allows us to control uniformly in \(\tau \) the norms of the extension of \({\mathcal {G}}_\tau f_\tau \) under the assumption that \({\mathcal {G}}_\tau f_\tau \) vanishes of infinite order at the origin and (ii) will follow (Proposition 6.5 ).
Let \(\tau \) be in \( {\widehat{K}}\) . There exist sequences \(\{C_m\}\) and \(\{N_m\}\) , independent of \(\tau \) and increasing, such that for every \(m\in {\mathbb {N}}\)
Let \(f_\tau \in {\mathcal {S}}(G)_{\tau }^{\textrm{Int}(K)}\) and \(F=A_\tau f_\tau \) . By ( 4.8 )
We recall that when \(n=3\) , then \(\kappa =1\) and the result is immediate. When \(n=4\) we have \(\kappa =2\) , but also \(\widehat{F}(-y)={\widehat{F}}(y)\) , for every \(y\in {\mathbb {R}}^4\) . Therefore the thesis follows easily from Propostition 2.4 . \(\square \)
We introduce the following notation for the derivatives at the origin of a function \(\psi \in {\mathcal {S}}(\Sigma _{\mathcal {D}}^\tau )\)
Note that the previous lemma gives estimates of \(c_{s,\tau , m}({\mathcal {G}}_\tau f_\tau )\) for each \( f_\tau \in {\mathcal {S}}(G)_{\tau }^{\textrm{Int}(K)}\) .
6.1 Control in \(\tau \) of derivatives at the origin
In this section we prove the following statement.
Proposition 6.2
Let \(f_\tau \) be in \({\mathcal {S}}(G)_{\tau }^{\textrm{Int}(K)}\) and u a smooth extension of \({\mathcal {G}}_\tau f_\tau \) to \({\mathbb {R}}^2\) . Then for every integer \(m\ge 0 \)
where the sequences \(\{C_{m}\}\) and \(\{N_{m}\}\) are independent of \(\tau \) and increasing.
The proof of Proposition 6.2 takes some effort. Indeed, its proof is rather technical and is based on relating (unknown) Maclaurin coefficients of any extension u up to order \(m\) with the (known) derivatives of \({\mathcal {G}}_\tau f_\tau \) along the curves defining the spectrum \(\Sigma ^\tau _{\mathcal {D}}\subset {\mathbb {R}}^2\) .
In doing so, for each order of derivation \(m\) , one obtains a (possibly overdetermined) linear system of the form
where the matrix \(\Lambda _{\tau ,m}\) is expressed in terms of the integers \(\beta _{s,\tau }\) and the vectors x and \(c_{\tau ,m}\) are related to \( \partial _1^{m-q}\partial _2^q u(0,0)\) and \(c_{s,\tau , m}({\mathcal {G}}_\tau f_\tau )\) , respectively. By Corollary 5.3 , this system is solvable; our task here is to describe the norm of x in terms of the norms of \(c_{\tau ,m}\) .
Estimates are split in Sects. 6.1.1 and 6.1.2 , dealing with the cases where \(n=4\) and \(n=3\) , respectively. In each case a special approach to the problem is used.
6.1.1 Proof of Proposition 6.2 when \(n=4\)
In this case, the expression of the integers \(\beta _{s,\tau }\) requires some additional work, starting from the following technical lemma.
Let \(n=4\) . For any positive integer \( d\le a_\tau \) there exists an integer \(\omega _{\tau ,d}\) such that if
Moreover \(|\omega _{\tau ,d}|\le d_\tau \) .
Let \(d\le a_\tau \) and \(s^*_{d}\) an index in \(\{0,1,\ldots d\}\) such that
Define \(\omega _{\tau ,d}:=\beta _{s^*_d,\tau }\) , then \(|\omega _{\tau ,d}|\) is an integer, no bigger than \(d_\tau \) .
Notice that for \(i=s^*_d\) we have \(\lambda _{i,\tau ,d}=\beta _{i,\tau }-\omega _{\tau ,d}=\beta _{i,\tau }-\beta _{s^*_d,\tau } =0\) , and \(\lambda _{i,\tau ,d}\) are nonzero integers when \(i\not =s^*_d\) . Then, for every s in \( \{0,1,\ldots d\ \}\) ,
We now continue the proof of Proposition 6.2 .
Fix \(\tau \in {\widehat{K}}\) and let \(f_\tau \in {\mathcal {S}}(G)_{\tau }^{\textrm{Int}(K)}\) and u a smooth extension of \({\mathcal {G}}_\tau f_\tau \) on \({\mathbb {R}}^2\) .
When \(m=0\) , the inequality follows from Lemma 6.1 . Given an order of derivation \(m> 0\) , let \(\omega _{\tau ,m}\) be as in Lemma 6.3 when \(m\in (0,{a_\tau }]\) and \(\omega _{\tau ,m}=\omega _{\tau ,{a_\tau }}\) when \(m>{a_\tau }\) . For each \(m> 0\) , define a smooth function \(v_m\) on \( {\mathbb {R}}^2\) by
so that, when \(t\ge 0\) and \(s=0,1,\dots ,a_\tau \) ,
be the Taylor expansion at the origin of the smooth function \(v_m\) . Our next goal is to write the Taylor coefficients \(a_{p,q}\) of \(v_m\) in terms of derivatives of \( {\mathcal {G}}_\tau f_\tau \) at the origin. For the sake of brevity, we write ( 6.1 ) as
and we have
Therefore we are led to solve the \(({a_\tau }+1)\times (m+1)\) linear system
Let \(m\le a_\tau \) . By Corollary 5.3 the system ( 6.2 ) is solvable, therefore we can consider the first \(m+1\) equations.
Denote by \(\Lambda \) the \((m+1)\times (m+1)\) matrix \(\Lambda =\big (\Lambda _{s,q}\big )=\big (\lambda _s^q\big )\) . Observe that \(\lambda _s\not =\lambda _j\) if \(s\not =j\) and that all maximal minors of \(\Lambda \) are essentially nonvanishing Vandermonde determinants. Thus, by Cramer’s rule,
where V is the full Vandermonde determinant with nodes \(\lambda _s \) and \(V_{s,q}\) are its cofactors. Expressing \(V_{s,q}\) in terms of Schur polynomials, cf. [ 11 ], by Lemma 6.3 we have
Hence by ( 6.3 ), ( 6.4 ) and Lemma 6.1
The case \(m> a_\tau \) can be reduced to the previous one by looking for a solution \(x=(x_0,x_1,\ldots ,x_{q},\ldots x_{m})\) with \(x_{q}=0\) for \(q>a_\tau \) .
6.1.2 Proof of Proposition 6.2 when \(n=3\)
When \(n=3\) we can slightly modify the arguments used for the complex motion group on \({\mathbb {C}}^2\) [ 4 ]. Indeed, in this case there is no need to use the technical Lemma 6.3 , so the proof is less involved. However, in order to have a solvable system of equations, one has to deal separately with the odd and the even part of \(F\in {\mathcal {S}}\big ({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) .
Given \(f_\tau \in {\mathcal {S}}(G)_{\tau }^{\textrm{Int}(K)}\) , let \(F=A_\tau f_\tau \) , and denote by \(F_-\) and \(F_+\) its odd and its even part, respectively. From Corollary 4.5 we have
Therefore we can restrict ourselves to consider \(s=\mu , \mu +1,\dots 2\mu \) corresponding to \(\beta _{s,\tau }=-\mu +s=0,1,\dots , \mu \) .
If u is a smooth extension of \({\mathcal {G}}_\tau f_\tau ={\mathcal {G}}_\tau ^\sharp F\) to \({\mathbb {R}}^2\) , straightforward computations show that the smooth functions \(u_-\) and \(u_+\) , defined by
extend \({\mathcal {G}}_\tau ^\sharp F_-\) and \({\mathcal {G}}_\tau ^\sharp F_+\) , respectively.
Let us consider the odd part first. If
is the Taylor expansion at the origin of \(u_-\) then \(a_{p,2q'}=0\) , for every \(p,q'\in {\mathbb {N}}\) , and the coefficients \(a_{p,q}\) must satisfy the equalities
so the equality in ( 6.5 ) for \(j=0\) is trivial. Moreover,
so the equalities ( 6.5 ) are trivial when \(m\) is even. Hence we write \(m=2\,m'+1\) , \(q=2q'+1\) and \(p=m'-q'\) and we obtain an \(\mu \times ( m'+1)\) linear system of the form
We now apply similar arguments to the even part \(F_+\in {\mathcal {S}}\big ({\mathbb {R}}^n,\textrm{End}({\mathcal {V}}_\tau )\big )^K\) . If
is the Maclaurin expansion of \(u_+\) then \( a_{p,2q'+1}=0 \) for every \(p, q'\in {\mathbb {N}}\) and the coefficients \(a_{p,q}\) must satisfy the equalities
Note that if m is odd and \(m=2p+q\) , then q is odd and \(a_{p,q}=0\) . Moreover
Hence the previous equalities ( 6.6 ) are trivial when \(m\) is odd. Thus we consider \(m=2\,m'\) , with \(m'\in {\mathbb {N}}\) and we observe that the equality in ( 6.6 ) for \(j=0\) reduces to
Therefore we are led to solve the \(\mu \times ( m'+1)\) linear system
It is now possible to follow the lines of the proof given for \(n=4\) in order to get the desired estimate. Note that the coefficients of the matrix \(\Lambda \) are \(\Lambda _{j,q}=(j^2)^q\) and an easy computation gives
which allows us to obtain the required estimates in the Vandermonde determinants. Thus the proof of Proposition 6.2 is complete.
6.2 Conclusion of the Proof of Theorem 1.1
In this section we prove condition (S’) of Theorem 1.2 adapting the arguments in [ 4 ]. We include here the proofs for reader’s convenience and we also correct some inaccuracies in the proof of [ 4 , Proposition 7.7].
We use a Borel argument to produce a smooth function with given Taylor’s coefficients at the origin and with controlled Schwartz norms up to some fixed order. Indeed, we observed in the proof of Proposition 6.2 that \(c_{s,\tau , m}({\mathcal {G}}_\tau f_\tau )\) are related to Maclaurin’s coefficients of any extension u of \({\mathcal {G}}_\tau f_\tau \) and in the same proposition we gave estimates for these coefficients. The following lemma is analogous to Lemma 7.6 in [ 4 ] and completes the proof of item (i) in the Introduction.
Let f be in \({\mathcal {S}}(G)^{\textrm{Int}(K)}\) and M in \({\mathbb {N}}\) . Then, for every \(\tau \in {\widehat{K}}\) there exists \(h_{\tau ,M}\) in \(C_c^\infty ({\mathbb {R}}^2)\) such that
and \(\Vert h_{\tau ,M}\Vert _{(M)}\) is rapidly decaying in \(\tau \) .
Let \(f\in {\mathcal {S}}(G)^{\textrm{Int}(K)}\) , \(M\in {\mathbb {N}}\) . Let \(\varphi \in C^\infty _c({\mathbb {R}}^2)\) supported in \(\{\xi \in {\mathbb {R}}^2\,\,:\,\, |\xi |\le 1\}\) and equal to 1 for \(|\xi |\le \frac{1}{2}\) . For any integers \(m,q\) with \(0\le q\le m\) let
Fix \(\tau \in {\widehat{K}}\) and let \(u_\tau \) be a smooth extension of \({\mathcal {G}}_\tau f_\tau \) to \({\mathbb {R}}^2\) . Following the standard Borel’s Lemma procedure, define
where the coefficients \(\varepsilon _m\in (0,1]\) will be chosen afterwards so that the series in ( 6.7 ) converges normally in every \(C^N\) -norm and \(\Vert h_{\tau ,M}\Vert _{(M)}\) decays rapidly in \(\tau \) .
By Proposition 6.2 , for every \(N\in {\mathbb {N}}\) ,
With \(\alpha _m=C_m\sum _{q=0}^m\Vert \psi _{m,q}\Vert _{C^{m-1}}\) , we choose
This implies that the series \(\sum _{m\in {\mathbb {N}}}\Vert h_m\Vert _{C^k}\) converges for every k , so that \(h_{\tau ,M}\) is smooth. Moreover, since the sequence \(\{N_{m}\}\) is increasing, then, for \(N\le M\) ,
where \(\displaystyle s_M=\sum \nolimits _{d\le M}\frac{ C_m}{m!}\, \sum \nolimits _{q=0}^m\Vert \psi _{m,q}\Vert _{C^M}\) . Hence, since \(\Vert f_\tau \Vert _{(N_M)}\) is rapidly decreasing in \(\tau \) , the function \(h_{\tau , M}\) defined in ( 6.7 ) with \(\varepsilon _m=\varepsilon _{m,\tau ,M}\) satisfies our requirements. \(\square \)
The following proposition is analogous to Proposition 7.7 in [ 4 ] and gives (ii) in the introduction.
Proposition 6.5
Let \(f_\tau \in {\mathcal {S}}(G)_{\tau }^{\textrm{Int}(K)}\) such that
Then \({\mathcal {G}}_\tau f_\tau \) can be extended to a Schwartz function \(v_\tau \) satisfying the following norm bounds: for every \(N\in {\mathbb {N}}\) there exist constants \(M_N\in {\mathbb {N}}\) and \(C_{N}>0\) , independent of \(\tau \) , such that
Let \(\eta \) be a bump function in \( C^\infty _c({\mathbb {R}})\) supported in \(\big (-\frac{1}{2}, \frac{1}{2}\big )\) and equal to 1 in a neighbourhood of the origin Let \(f_\tau \in {\mathcal {S}}(G)_{\tau }^{\textrm{Int}(K)}\) and define \(v_\tau \) on \({\mathbb {R}}^2\) by the rule
It is straightforward to show that \(v_\tau \) extends \( {\mathcal {G}}_\tau f_\tau \) to \({\mathbb {R}}^2\) . We now show that \(v_\tau \) is smooth and that for every \(N\in {\mathbb {N}}\) there exist constants \(M_N\in {\mathbb {N}}\) and \(C_{N}>0\) , independent of \(\tau \) , such that
One can check by induction that, for appropriate coefficients \(a_{r,h,q}\)
Now fix \((\xi _1,\xi _2)\) with \(\xi _1>0\) close enough to the spectrum so that there exists s such that \(\left| \frac{\xi _2}{\xi _1^{\kappa /2}}- \beta _{s,\tau }\right| <\frac{1}{2}. \) Then the sum defining \(v_\tau \) reduces to a single term and
Therefore we need to estimate
for every integer \(N\ge 0\) when \(\left| \frac{\xi _2}{\xi _1^{\kappa /2}}- \beta _{s,\tau }\right| <\frac{1}{2}.\)
Thus the expression in ( 6.8 ) can be controlled by a linear combination, independent of \(\tau \) , of terms of the type
where \(\alpha ,\beta ,\gamma ,\ell \) are non negative integers.
Since \(g(\xi _1)={\mathcal {G}}_\tau (\Delta ^\beta \,{\textbf{D}}_\tau ^\gamma f)(\xi _1^{2/\kappa }, \beta _{s,\tau }\xi _1)\) vanishes of infinite order at the origin, for any integer \(q\ge 0\) there exists \(\theta \in (0,1)\) such that for any \(\xi _1> 0\)
Therefore, in view of Lemma 6.1 , \(v_\tau \in C^\infty ({\mathbb {R}}^2)\) and the required norm estimates follow. \(\square \)
Finally we collect all our results in order to produce an extension with norms rapidly decaying in \(\tau \) , so proving the Schwartz correspondence for \(\big (M_n({\mathbb {R}}),SO_n\big )\) according to Theorem 1.2 . Given f in \({\mathcal {S}}(G)^{\textrm{Int}(K)}\) and \(\tau \) in \( {\widehat{K}}\) , we have \({\mathcal {G}}f_\tau (\xi '_\tau ,\xi '') ={\mathcal {G}}_{\tau } f_\tau (\xi '') \) , hence condition (S’) is equivalent to the following.
Proposition 6.6
Let f be in \({\mathcal {S}}(G)^{\textrm{Int}(K)}\) and N in \({\mathbb {N}}\) . Then, for every \(\tau \in {\widehat{K}}\) , \({\mathcal {G}}_{\tau } f_\tau \) admits a Schwartz extension \(u_{\tau ,N}\) from \(\Sigma _{\mathcal {D}}^\tau \) to \({\mathbb {R}}^2\) such that \(\Vert u_{\tau ,N}\Vert _{(N)}\) is rapidly decaying in \(\tau \) .
Let f be in \({\mathcal {S}}(G)^{\textrm{Int}(K)}\) , \(\tau \in {\widehat{K}}\) and \(N\in {\mathbb {N}}\) . For M to be chosen afterwards, let \(h_{\tau ,M}\) be the function associated to \(f_\tau \) , according to Lemma 6.4 . By Corollary 2.2 there exists \(g_{\tau ,M}\in {\mathcal {S}}(G)_{\tau }^{\textrm{Int}(K)}\) such that \({\mathcal {G}}_\tau g_{\tau ,M}= \left( h_{\tau ,M}\right) _{|_{\Sigma _{\mathcal {D}}^\tau }}. \) Since
by Proposition 6.5 ,here exists an extension \(v_{\tau ,M}\) of \({\mathcal {G}}_\tau (f_\tau - g_{\tau ,M})\) and a positive integer \(N'\) , depending only on N , such that
By Corollary 2.2 , there exists \(N''\) , depending on \(N'\) , such that
where the constant \(C_{\tau ,N}\) has polynomial growth in \(\tau \) . Choose M bigger than N and \(N''\) , then
is a Schwartz extension to \({\mathbb {R}}^2\) of \({\mathcal {G}}_\tau f_\tau \) whose N -Schwartz norm decays rapidly in \(\tau \) . Indeed,
where the constant \(C'_{\tau ,N}\) has polynomial growth in \(\tau \) and both \(\Vert f_\tau \Vert _{(N')}\) and \(\Vert h_{\tau ,M} \Vert _{(M)} \) decay rapidly in \(\tau \) . \(\square \)
Data availability
We do not analyse or generate any datasets, because our work proceeds within a theoretical and mathematical approach.
Astengo, F., Di Blasio, B., Ricci, F.: Gelfand transforms of polyradial Schwartz functions on the Heisenberg group. J. Funct. Anal. 251 , 772–791 (2007)
Article MathSciNet Google Scholar
Astengo, F., Di Blasio, B., Ricci, F.: Gelfand pairs on the Heisenberg group and Schwartz functions. J. Funct. Anal. 256 , 1565–1587 (2009)
Astengo, F., Di Blasio, B., Ricci, F.: On the Schwartz correspondence for Gelfand pairs of polynomial growth. Rend. Lincei Mat. Appl 32 , 79–96 (2021)
MathSciNet Google Scholar
Astengo, F., Di Blasio, B., Ricci, F.: Schwartz correspondence for the complex motion group on \({\mathbb{C}}^2\)
Benson, C., Jenkins, J., Ratcliff, G.: On Gelfand pairs associated with solvable Lie groups. Trans. Am. Math. Soc. 321 , 85–116 (1990)
Benson, C., Jenkins, J., Ratcliff, G.: The spherical transform of a Schwartz function on the Heisenberg group. J. Funct. Anal. 154 , 379–423 (1998)
Ferrari Ruffino, F.: The topology of the spectrum for Gelfand pairs on Lie groups. Boll. Unione Mat. Ital. B 10 , 569–579 (2007)
Fischer, V., Ricci, F.: Gelfand transforms of \(SO(3)\) -invariant Schwartz functions on the free group \(N_{3,2}\) . Ann. Inst. Four. Gren. 59 , 2143–2168 (2009)
Article Google Scholar
Fischer, V., Ricci, F., Yakimova, O.: Nilpotent Gelfand pairs and spherical transforms of Schwartz functions I: rank-one actions on the centre. Math. Z. 271 , 221–255 (2012)
Fischer, V., Ricci, F., Yakimova, O.: Nilpotent Gelfand pairs and Schwartz extensions of spherical transforms via quotient pairs. J. Funct. Anal. 274 , 1076–1128 (2018)
Fulton, W., Harris, J.: Representation Theory. A First Course, Graduate Texts in Mathematics, vol. 129. Springer (1991)
Google Scholar
Gelfand, I.M.: Spherical functions in symmetric Riemann spaces. Dokl. Akad. Nauk SSSR 70 , 5–8 (1950)
Kaplan, A., Ricci, F.: Harmonic analysis on groups of Heisenberg type. In: Lecture Notes in Mathematics, vol. 992, pp. 416–435. Springer, Berlin (1983)
Lauret, J.: Homogeneous nilmanifolds attached to representations of compact Lie groups. Manuscripta Math. 99 , 287–309 (1999)
Lauret, J.: Gelfand pairs attached to representations of compact Lie groups. Transform. Groups 5 , 307–324 (2000)
Martini, A.: Algebras of differential operators on Lie groups and spectral multipliers, Ph.D. Thesis, Scuola Norm. Sup. Pisa (2010), arXiv:1007.1119
Nestruev, J.: Smooth Manifolds and Observables, Graduate Texts in Mathematics, vol. 220. Springer-Verlag, New York (2003)
Nelson, E., Steinspring, W.: Representation of elliptic operators in an enveloping algebra Amer. J. Math. 81 , 547–560 (1959)
Ricci, F.: Commutative algebras of invariant functions on groups of Heisenberg type. J. Lond. Math. Soc. 32 , 265–271 (1985)
Ricci, F., Samanta, A.: Spherical analysis on homogeneous vector bundles. Adv. Math. 338 , 953–990 (2018)
Varadarajan, V.S.: Lie Groups, Lie Algebras, and Their Representations, Graduate Texts in Mathematics. Springer-Verlag, New York (1984)
Book Google Scholar
Vinberg, E.: Commutative homogeneous spaces and co-isotropic symplectic actions. Russ. Math. Surv. 56 , 1–60 (2001)
Wolf, J.: Harmonic Analysis on Commutative Spaces, Mathematical Surveys and Monographs, vol. 142. AMS (2007)
Yakimova, O.: Principal Gelfand pairs. Transform. Groups 11 , 305–335 (2006)
Download references
Open access funding provided by Scuola Normale Superiore within the CRUI-CARE Agreement.
Author information
Authors and affiliations.
Dipartimento di Matematica, Dipartimento di Eccellenza 2023–2027, Università di Genova, Via Dodecaneso 35, 16146, Genoa, Italy
Francesca Astengo
Dipartimento di Matematica e Applicazioni, Università di Milano Bicocca, Via Cozzi 53, 20125, Milan, Italy
Bianca Di Blasio
Scuola Normale Superiore, Piazza dei Cavalieri 7, 56126, Pisa, Italy
Fulvio Ricci
You can also search for this author in PubMed Google Scholar
Contributions
The work has been developed jointly by the three authors in all its parts. We have read the Nature Portfolio journal policies on author responsibilities and submit this manuscript in accordance with those policies.
Corresponding author
Correspondence to Fulvio Ricci .
Ethics declarations
Conflict of interest.
The authors declare that they have no conflict of interest.
Ethics approval and consent to participate
This manuscript has not and will not be submitted to more than one journal for simultaneous consideration. The submitted work is original and will not be published elsewhere.
Consent for publication
We agree that this manuscript will be published in the “Annals of Global Analysis and Geometry”.
Additional information
Publisher's note.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .
Reprints and permissions
About this article
Astengo, F., Di Blasio, B. & Ricci, F. Schwartz correspondence for real motion groups in low dimensions. Ann Glob Anal Geom 66 , 5 (2024). https://doi.org/10.1007/s10455-024-09963-y
Download citation
Received : 23 February 2024
Accepted : 19 July 2024
Published : 29 July 2024
DOI : https://doi.org/10.1007/s10455-024-09963-y
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Groups of polynomial growth
- Gelfand pairs
- Spherical transform
- Schwartz space
Mathematics Subject Classification
- Find a journal
- Publish with us
- Track your research
- Corpus ID: 271600555
The synthetic presentation of the main research directions in groupoid theory
- Gheorghe Ivan
- Published 1 August 2024
- Mathematics
73 References
Lie groupoids and lie algebroids in differential geometry.
- Highly Influential
Search by keyword
Gdp up by 0.3% in both the euro area and the eu, announcement.
Following recommendations for a harmonised European revision policy for national accounts and balance of payments , EU countries will carry out a benchmark revision of their national accounts estimates in 2024. The purpose of this benchmark revision is to implement changes introduced by the amended ESA 2010 regulation , and to incorporate new data sources and other methodological improvements. Most of the revised quarterly and annual country data are expected to be released by Eurostat between June and October 2024, and will be progressively integrated in European estimates. The impact of these revisions is expected to be limited, but still noticeable for some European aggregates and more pronounced for certain Member States. For further details, please consult the available documentation on Eurostat’s website .
In the second quarter of 2024, seasonally adjusted GDP increased by 0.3% in both the euro area and the EU , compared with the previous quarter, according to a preliminary flash estimate published by Eurostat, the statistical office of the European Union . In the first quarter of 2024, GDP had also grown by 0.3% in both zones.
These preliminary GDP flash estimates are based on data sources that are incomplete and subject to further revisions.
Compared with the same quarter of the previous year, seasonally adjusted GDP increased by 0.6% in the euro area and by 0.7% in the EU in the second quarter of 2024, after +0.5% in the euro area and +0.6% in the EU in the previous quarter.
Among the Member States for which data are available for the second quarter of 2024, Ireland (+1.2%) recorded the highest increase compared to the previous quarter, followed by Lithuania (+0.9%) and Spain (+0.8%). The highest declines were recorded in Latvia (-1.1%), Sweden (-0.8%) and Hungary (-0.2%). The year on year growth rates were positive for eight countries and negative for three.
Published growth rates of GDP in volume up to 2024Q2 (based on seasonally adjusted* data) | ||||||||
|---|---|---|---|---|---|---|---|---|
Percentage change compared with the previous quarter | Percentage change compared with the same quarter of the previous year | |||||||
2023Q3 | 2023Q4 | 2024Q1 | 2024Q2 | 2023Q3 | 2023Q4 | 2024Q1 | 2024Q2 | |
Euro area | 0.0 | 0.0 | 0.3 |
| 0.1 | 0.2 | 0.5 |
|
EU | 0.1 | 0.0 | 0.3 |
| 0.2 | 0.4 | 0.6 |
|
Belgium | 0.3 | 0.3 | 0.3 |
| 1.3 | 1.3 | 1.3 |
|
Czechia | -0.4 | 0.3 | 0.2 |
| -0.4 | 0.0 | 0.3 |
|
Germany | 0.2 | -0.4 | 0.2 |
| -0.3 | -0.2 | -0.1 |
|
Ireland | -1.7 | -1.5 | 0.7 |
| -8.3 | -9.8 | -4.0 |
|
Spain | 0.5 | 0.7 | 0.8 |
| 1.9 | 2.2 | 2.6 |
|
France | 0.1 | 0.4 | 0.3 |
| 0.9 | 1.3 | 1.5 |
|
Italy | 0.3 | 0.1 | 0.3 |
| 0.6 | 0.7 | 0.6 |
|
Latvia | -0.3 | 0.3 | 0.8 |
| 0.2 | -0.2 | 0.8 |
|
Lithuania | -0.1 | -0.2 | 0.9 |
| 0.1 | 0.1 | 3.0 |
|
Hungary | 0.8 | 0.0 | 0.7 |
| -0.2 | 0.5 | 1.6 |
|
Austria | -0.2 | 0.1 | 0.2 |
| -1.7 | -1.3 | -1.3 |
|
Portugal | -0.2 | 0.7 | 0.8 |
| 1.9 | 2.1 | 1.5 |
|
Sweden** | 0.2 | 0.3 | 0.5 |
| -0.7 | -0.1 | 0.7 |
|
* Growth rates to the previous quarter and to the same quarter of the previous year presented in this table are both based on seasonally and calendar adjusted figures, except where indicated. Unadjusted data are not available for all Member States that are included in GDP flash estimates. ** Percentage change compared with the same quarter of the previous year calculated from calendar adjusted data. Source dataset:
| ||||||||
The next estimates for the second quarter of 2024 will be released on 14 August 2024.
Notes for users
The reliability of GDP flash estimates was tested by dedicated working groups and revisions of subsequent estimates are continuously monitored . Further information can be found on Eurostat website .
With this preliminary flash estimate, euro area and EU GDP figures for earlier quarters are not revised.
All figures presented in this release may be revised with the GDP t+45 flash estimate scheduled for 14 August 2024 and subsequently by Eurostat’s regular estimates of GDP and main aggregates (including employment) scheduled for 6 September 2024 and 18 October 2024, which will reflect the impact of countries’ benchmark revisions as available.
The preliminary flash estimate of GDP growth for the second quarter of 2024 presented in this release is based on the data of 18 Member States, covering 96% of euro area GDP and 94% of EU GDP.
Release schedule
Comprehensive estimates of European main aggregates (including GDP and employment) are based on countries regular transmissions and published around 65 and 110 days after the end of each quarter. To improve the timeliness of key indicators, Eurostat also publishes flash estimates for GDP (after around 30 and 45 days) and employment (after around 45 days). Their compilation is based on estimates provided by EU Member States on a voluntary basis.
This news release presents preliminary flash estimates for euro area and EU after around 30 days.
Methods and definitions
European quarterly national accounts are compiled in accordance with the European System of Accounts 2010 (ESA 2010).
Gross domestic product (GDP) at market prices measures the production activity of resident production units. Growth rates are based on chain-linked volumes.
Two statistical working papers present the preliminary GDP flash methodology for the European estimates and Member States estimates .
The method used for compilation of European GDP is the same as for previous releases.
Geographical information
Euro area (EA20): Belgium, Germany, Estonia, Ireland, Greece, Spain, France, Croatia, Italy, Cyprus, Latvia, Lithuania, Luxembourg, Malta, the Netherlands, Austria, Portugal, Slovenia, Slovakia and Finland.
European Union (EU27): Belgium, Bulgaria, Czechia, Denmark, Germany, Estonia, Ireland, Greece, Spain, France, Croatia, Italy, Cyprus, Latvia, Lithuania, Luxembourg, Hungary, Malta, the Netherlands, Austria, Poland, Portugal, Romania, Slovenia, Slovakia, Finland and Sweden.
For more information
Website section on national accounts , and specifically the page on quarterly national accounts
Database section on national accounts and metadata on quarterly national accounts
Statistics Explained articles on measuring quarterly GDP and presentation of updated quarterly estimates
Country specific metadata
Country specific metadata on the recording of Ukrainian refugees in main aggregates of national accounts
European System of Accounts 2010
Euro indicators dashboard
Release calendar for Euro indicators
European Statistics Code of Practice
Get in touch
Media requests
Eurostat Media Support
Phone: (+352) 4301 33 408
E-mail: [email protected]
Further information on data
Thierry COURTEL
Johannes BUCK
E-mail: [email protected]
Share the release
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
find presentation of semidirect product (C2 x C2) ⋊ C2
I would really appreciate a step by step about how to solve the following:
C2 rwr C2 (where rwr is the regular wreath product)
i know it becomes ( C2 x C2 ) ⋊ C2 , so how to go from here.
edit: with solve i mean find the presentation of C2 rwr C2 .
- abstract-algebra
- group-theory
- $\begingroup$ What do you mean precisely(!) by "solve" or "calculate"? $\endgroup$ – Martin Brandenburg Commented Nov 13, 2012 at 13:25
- $\begingroup$ ah yeah i missed that. edited. $\endgroup$ – grendizer Commented Nov 13, 2012 at 13:31
- $\begingroup$ anyone who can help? $\endgroup$ – grendizer Commented Nov 14, 2012 at 8:46
- $\begingroup$ Start by writing down presentations of $C_2 \times C_2$, and of $C_2$. Can you do that? $\endgroup$ – Derek Holt Commented Nov 15, 2012 at 19:36
- $\begingroup$ for C2 = < X | X^2 = 1 > and the other C2 = < Y | Y^2 = 1 >, the presentation of C2 x C2 will be < X,Y | X^2 = 1, Y^2 = 1, XY = YX > $\endgroup$ – grendizer Commented Nov 16, 2012 at 8:49
So for the base group $C_2 \times C_2$ you have the presentation $\langle X,Y \mid X^2=Y^2=1, XY=YX \rangle$, which you correctly wrote down.
For the complement $C_2$, you should choose another letter for the generator, so make it $\langle Z \mid Z^2 = 1\rangle$.
To get the presentation of the wreath product, we combine these and use generators $X,Y,Z$ with all the relations you have already. But we need some extra relations which specify the action by conjugation of $C_2$ on $C_2 \times C_2$. Since this action is uniquely specified by the actions of generators on generators, you need just two further relations, which will be of the form
$Z^{-1}XZ = w_1$ and $Z^{-1}YZ = w_2$,
where $w_1$ and $w_2$ are elements of $C_2 \times C_2$, which you need to specify as words in the generators $X,Y$. I have left you to figure out what $w_1$ and $w_2$ should be.
- $\begingroup$ w1 = X^-1 and w2 = Y^-1 $\endgroup$ – grendizer Commented Nov 16, 2012 at 15:32
- 1 $\begingroup$ No - don't forget that all of these generators have order 2, so $X^{-1}=X$. The action in the wreath product is to interchange the to $C_2$s, so you want $Z^{-1}XZ=Y$ and $Z^{-1}YZ=X$. $\endgroup$ – Derek Holt Commented Nov 16, 2012 at 19:25
- $\begingroup$ ah ok. thank a lot for your help. $\endgroup$ – grendizer Commented Nov 17, 2012 at 8:27
You must log in to answer this question.
Not the answer you're looking for browse other questions tagged abstract-algebra group-theory ..
- Featured on Meta
- Announcing a change to the data-dump process
- We've made changes to our Terms of Service & Privacy Policy - July 2024
- Upcoming Moderator Election
- 2024 Moderator Election Q&A – Question Collection
Hot Network Questions
- Could Swashplate be replaced with small electric motors?
- The existence of an eigenvalue of a finite-dim matrix, in a vector space over an arbitrary field.
- Applications take a few seconds to open, but only the first time I open them
- Is it correct to say: "To solve an addiction"?
- Is it safe to keep an expired credit card?
- "make / work / find one's way to somewhere"
- Child's teddies "being mean" after dark
- Singed Random Numbers
- How to make an operator form of Part[] to use with // (Postfix)
- Split column into lines using awk
- Was the idea of foxes with many tails invented in anime, or is it a Japanese folk religion thing?
- How can I make a PAL sync generator without a microcontroller?
- Can an exponentially growing population perform eugenics and selective breeding at short time scales?
- How does Wild Shape interact with the clone spell?
- Is there any family history for Klaus Stortebeker?
- How long should I boil a liquid mixture containing vanilla extract to vaporize the alcohol, when making ice cream?
- Is "Non-Trivial amount of work" a correct phrase?
- What is the timescale for "$ Change" and "% Change" on Vanguard's Holdings page?
- Efficient way to remove nailed-down plywood flooring in attic without damaging it?
- Why have SIGPIPE when EPIPE exists?
- How can I count frequency of a list faster?
- How to use the すぎ suffix to mean "too much"?
- How much does having competing offers benefit a job search?
- ESTA renewal advice

An official website of the United States government
Here’s how you know
Official websites use .gov A .gov website belongs to an official government organization in the United States.
Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you’ve safely connected to the .gov website. Share sensitive information only on official, secure websites.

Site branding
Header - callout.
In Crisis? Call or Text 988
Solr Mobile Search
Page title - second level, view cart button.
Your browser is not supported
Switch to Chrome, Edge, Firefox or Safari
Store Navigation - Start New Search
Main page content, results from the 2023 national survey on drug use and health (nsduh).

This report provides key findings from the 2023 National Survey on Drug Use and Health (NSDUH) on substance use, mental health, and treatment among the noninstitutionalized U.S. population aged 12 or older. Estimates are presented by age group and by race/ethnicity for selected measures.
Units per Product
2023 NSDUH Annual National Report File Type: PDF File Size: 2.65 MB
Companion Infographic Report File Type: PDF File Size: 706 KB
Companion Report On Race/Ethnicity File Type: PDF File Size: 1.27 MB
Find Related Information
Audience: Policymakers , Program Planners, Administrators, & Project Managers , Public Health Professionals , Researchers
You May Also Be Interested In

Results from the 2022 National Survey on Drug Use and Health (NSDUH): Key Substance Use and Mental Health Indicators in the United States
This report provides key findings from the 2022 National Survey on Drug Use and Health (NSDUH) on substance use, mental health, and treatment among the noninstitutionalized U.S. population aged 12 or older. Estimates are presented by age group and by race/ethnicity for selected measures.

National Substance Use and Mental Health Services Survey (N-SUMHSS) 2022: Data on Substance Use and Mental Health Treatment Facilities
The N-SUMHSS is a voluntary annual survey of all active substance use and mental health facilities in the United States, its territories, and D.C. The annual report presents findings on the key operational characteristics of substance use and mental health treatment facilities, use of pharmacotherapies, language assistance services, and suicide prevention assistance services.

Drug Abuse Warning Network (DAWN): Findings from Drug-Related Emergency Department Visits 2022
An analysis of the 2022 DAWN data presents nationally representative weighted estimates of all drug-related emergency department (ED) visits, nationally representative weighted estimates of the top substances involved in drug-related ED visits, including rates by race and ethnicity; nationally representative weighted estimates of opioid- related ED visits by type of opioid, drugs involved in polysubstance ED visits, and the identification of newly mentioned drugs in 2022.

Mental Health Client-Level Data (MH-CLD) 2022: Data on Clients Receiving Mental Health Treatment Services Through State Mental Health Agencies
Mental Health Client-Level Data (MH-CLD) 2022: Data on Clients Receiving Mental Health Treatment Services Through State Mental Health Agencies annual report presents the total number of clients receiving mental health treatment services in 2022 by demographics, National Outcome Measures (NOMs), and the top five mental health diagnoses for children (ages 0-17) and adults (ages 18 and older) by geographic distribution, and a summary of client characteristics for the 2018-2022 reporting periods.

Behavioral Health Barometers, Region 1-10, Volume 7: Indicators as Measured in the 2021-2022 National Surveys on Drug Use and Health

BestPractices4Data: Sharing Innovations and Best Practice for Grantees, from Grantees

COMMENTS
But if I were to give a brief explanation, conjugation defines a group action (i.e. k ⋅ h = khk−1 k ⋅ h = k h k − 1 is a well-defined group action). Since the semidirect product is a group we're looking to construct -- that is, we have yet shown that such a group exists prior to construction -- technically the multiplication of elements ...
Semidirect products Examples of semidirect products In other words, inside N oH the homomorphism r : H !Aut(N) corresponds to conjugation of N by H. The group N oH is called the semidirect product of N and H. The roles of N and H cannot be exchanged. Example For any cyclic group Z n, there is a homomorphism r : f 1g!Aut(Z n): r( 1)(x) = x: n.
SEMIDIRECT PRODUCTS 3 3. Semidirect products When Hand Kare subgroups of a group G, the set-product HKmight not be a subgroup. For example, in S 3 if H= h(12)iand K= h(13)ithen HK= f(1);(12);(13);(132)ghas size 4 and is not a subgroup of S 3. However, if Hor Kis normal in Gthen HKis a subgroup. Taking HCG, for instance,
a semidirect product. Conversely, if G is a semidirect product, then K has a complement H and the inverse of the isomorphism `: H ! Q is a section s. Definition 10.9. Suppose that µ: Q ! Aut(K) (x 7!µx) is a homomor-phism. Then we say that a semidirect product G of K by Q realizes µ if the conjugation action of H = s(Q) on K is given by µ ...
In mathematics, specifically in group theory, the concept of a semidirect product is a generalization of a direct product.There are two closely related concepts of semidirect product: an inner semidirect product is a particular way in which a group can be made up of two subgroups, one of which is a normal subgroup.; an outer semidirect product is a way to construct a new group from two given ...
In group theory, a semidirect product is a generalization of the direct product which expresses a group as a product of subgroups. There are two ways to think of the construction. One is intrinsic: the condition that a given group \ (G\) is a semidirect product of two given subgroups \ (N\) and \ (H\) is equivalent to some special conditions on ...
rect product of H a. d K.2. Semidirect ProductsSuppose now we relax the rst condition, so that H is still no. mal in G but K need not be. We retain the other conditions. normal in G,H \ K = f1g,HK = G, In this case we obtain what is. lled a semidirect product.Examples: uppose H = Z=3 and K = Z=2. There is more.
Semidirect products are a very useful rudiment of nite group theory, but the diffi-culties in working with them are often both under- and over-estimated. This document attempts to handle some of these issues. A motivating example describe the semi-direct products of S3 by S3. In this case we get 3 conjugacy classes of actions f S3 Aut S3, but ...
where , , and (Suzuki 1982, p. 67; Scott 1987, p. 213). Note that the semidirect product of two groups is not uniquely defined.. The semidirect product of a group by a group can also be defined as a group which is the product of its subgroups and , where is normal in and .If is also normal in , then the semidirect product becomes a group direct product (Shmel'kin 1988, p. 247).
2. Verify that N ˚His the internal semi-direct product of the subgroups Nf e Hgand fe Ng H. 3. Show that the multiplication in a semi-direct product is the same as the product in a direct product if and only if ˚is trivial, meaning ˚ his the identity in Aut(N) for all h, meaning that for all hand n, ˚ h(n) = n. 4.
All semidirect products of K by Harise this way. The trivial homomorphism u(h) = id, for all h2H, yields the direct product group K H. If there are no non-trivial homomorphisms u: H!Aut(K), then the direct product is the only semidirect product of Kby H. There is an action of the group Aut(H) Aut(K) on the set Hom(H;Aut(K)). If ais an
The last exercises return to the case of a nonabelian group and multiplicative notation to remedy an omission: we have notions of an internal and external direct product, but we have only defined the notion of an internal semidirectproduct. The external semidirect product is an important construction, but requires a bit more data.
The semidirect product is called the dihedral group D_{2 n}. ... for that, we relied on the the semidirect product. For example, here is a presentation of the nonabelian group with 21 elements. (See Exercise 1.3.23 and Proposition 1.7.1 below.) The group G has generators x and y with relations x^7 = y^3 = 1 and y x y^ ...
If you have explicit finite presentations of G and H is small and finite, then you should be able to just ask GAP or magma for a presentation of the kernel of the projection. This is another disguise of the Schreier transversal. Let me know if you want code sample or algorithmic references.
Theorem 5. Suppose G is a group with subgroups H and Q, and G is the internal semi-direct product of H and Q. Then G ≅ H ⋊θQ where θ: Q Aut(H) is given by. θ(q)(h) := qhq - 1, q ∈ Q, h ∈ H. Proof. By Lemma 4, every element g of G can be written uniquely in the form hq, with h ∈ H and q ∈ Q. Therefore, the map ϕ: H ⋊ Q G ...
$\begingroup$ It is proved in Section 10.2 of the book "Presentations of Groups" by D.L. Johnson, The result proved there is more general and covers all extensions, not just semidirect products. But the proof is not exactly difficult! $\endgroup$
Theorem. A set U U of elements of the semidirect product G = NK G = N K with N G N G is a subgroup of G G if and only if. UN ∩ K U N ∩ K and U ∩ K U ∩ K are subgroups of G G; U ∩ N U ∩ N is a subgroup and UK ∩ N U K ∩ N is a collection of U ∩ N U ∩ N -cosets in N N; and.
presentation of some ways of building up new groupoids from old ones, for instance: direct product of a familly of groupoids ([31]), semidirect product and solvable groupoid ([63]). ... direct products, semidirect products andsolvability, Algebra and Discrete Math., 33(2) (2022), 92-107. Doi:10.12958/adm 1772 ...
If G has polynomial volume growth (in which case we also say that the pair (G, K) has polynomial growth) and the chosen generators \(D_j\in {\mathcal {D}}\) are symmetric, the eigenvalues are real, so that \(\Sigma _{\mathcal {D}}\subset {\mathbb {R}}^\ell \).We refer to [] for a presentation of Gelfand pairs of polynomial growth and the proofs of various preliminary results that will be used ...
The product of two such matrices g (x 1, y 1, ... Of the 65 Sohncke groups, most (but not all) can be written as a semidirect product of a Bieberbach group and a subgroup of the concrete point group of the form ... which enriched this presentation, and Professor D. Zlatanov for initially suggesting an investigation of this kind. ...
Unfortunately, I can't get the book "Presentations of Groups" by D.L. Johnson where it's said that this is proved. Any help will be greatly appreciated! abstract-algebra
The purpose of this paper is to present a systematic exposition of the main results obtained in the studies carried out in groupoid theory. Key words and phrases: groupoid, topological groupoid, Lie groupoid, group-groupoid, vector space-groupoid.
Statistics Explained articles on measuring quarterly GDP and presentation of updated quarterly estimates. Country specific metadata. Country specific metadata on the recording of Ukrainian refugees in main aggregates of national accounts. European System of Accounts 2010. Euro indicators dashboard. Release calendar for Euro indicators
C2 rwr C2 (where rwr is the regular wreath product) i know it becomes ( C2 x C2 ) ⋊ C2 , so how to go from here. edit: with solve i mean find the presentation of C2 rwr C2 .
This report provides key findings from the 2023 National Survey on Drug Use and Health (NSDUH) on substance use, mental health, and treatment among the noninstitutionalized U.S. population aged 12 or older. Estimates are presented by age group and by race/ethnicity for selected measures.