- Explore Programs
- Visit Campus
- Request Info
- Work at UTRGV
- Faculty Resources
- Staff Resources

Page Not Found
Sorry, the page you are looking for cannot be found and might have been removed, had its name changed, or is temporarily unavailable. It is recommended that you start again from the homepage. Feel free to contact us if the problem persists or if you definitely cannot find what you’re looking for.
Here are some suggested sites
- PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
- EDIT Edit this Article
- EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Happiness Hub Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
- Browse Articles
- Learn Something New
- Quizzes Hot
- Happiness Hub
- This Or That Game
- Train Your Brain
- Explore More
- Support wikiHow
- About wikiHow
- Log in / Sign up
- Education and Communications
- Mathematics
How to Find the Domain and Range of a Function
Last Updated: January 25, 2024 Fact Checked
This article was co-authored by David Jia . David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 341,966 times.
Every function contains two types of variables: independent variables and dependent variables, whose values literally “depend” on the independent variables. For example, in the function y = f ( x ) = 2 x + y , x is independent and y is dependent (in other words, y is a function of x ). The valid values for a given independent variable x are collectively called the “domain.” The valid values for a given dependent variable y are collectively called the “range.” [1] X Research source
Finding the Domain of a Function

- A quadratic function has the form ax 2 + bx + c: f(x) = 2x 2 + 3x + 4
- Examples of functions with fractions include: f(x) = ( 1 / x ), f(x) = (x + 1) / (x - 1) , etc.
- Functions with a root include: f(x) = √x, f(x) = √(x 2 + 1), f(x) = √-x, etc.

- For example, a domain of [-2, 10) U (10, 2] includes -2 and 2, but does not include number 10.
- Always use parentheses if you are a using the infinity symbol, ∞. This is because infinity is a concept and not a number.

- To get an idea of the function choose any x-value and plug it into the function. Solving the function with this x-value will output a y-value. These x- and y-values are a coordinate (x, y) of the graph of the function.
- Plot this coordinate and repeat the process with another x-value.
- Plotting a few values in this fashion should give you a general idea of shape of the quadratic function.

- For example: Identify the domain of the function f(x) = (x + 1) / (x - 1) .
- The denominator of this function is (x - 1).
- Set it equal to zero and solve for x: x – 1 = 0, x = 1.
- Write the domain: The domain of this function cannot include 1, but includes all real numbers except 1; therefore, the domain is (-∞, 1) U (1, ∞).
- (-∞, 1) U (1, ∞) can be read as the set of all real numbers excluding 1.The infinity symbol, ∞, represents all real numbers. In this case, all real numbers greater than 1 and less than one are included in the domain.

- For example: Identify the domain of the function f(x) = √(x + 3).
- The terms within the radical are (x + 3).
- Set them greater than or equal to zero: (x + 3) ≥ 0.
- Solve for x: x ≥ -3.
- The domain of this function includes all real numbers greater than or equal to -3; therefore, the domain is [-3, ∞).
Finding the Range of a Quadratic Function

- The easiest way to identify the range of other functions, such as root and fraction functions, is to draw the graph of the function using a graphing calculator.

- For example, find the range of 3x 2 + 6x -2.
- Calculate x-coordinate of vertex: x = -b/2a = -6/(2*3) = -1

- Calculate y-coordinate: y = 3x 2 + 6x – 2 = 3(-1) 2 + 6(-1) -2 = -5.
- The vertex of this function is (-1, -5).

- Use the x-value -2: y = 3x 2 + 6x – 2 = y = 3(-2) 2 + 6(-2) – 2 = 12 -12 -2 = -2.
- This yields the coordinate (-2, -2).
- This coordinate tells you that the parabola continues above the vertex (-1, -5); therefore, the range encompasses all y-values above -5.
- The range of this function is [-5, ∞)

- For example, a range of [-2, 10) U (10, 2] includes -2 and 2, but does not include number 10.
- Always use parentheses if you are a using the infinity symbol, ∞.
Finding the Range of a Function Graphically

- Some root functions will start above or below the x-axis. In this case, the range is determined by the point the root function starts. If the parabola starts at y = -4 and goes up, then the range is [-4, +∞).
- The easiest way to graph a function is to use a graphing program or a graphing calculator.
- If you do not have a graphing calculator, you can draw a rough sketch of a graph by plugging x-values into the function and getting the corresponding y-values. Plot these coordinates on the graph to get an idea of the shape of the graph.

- A fraction function will include all points except those at the asymptote. They often have ranges such as (-∞, 6) U (6, ∞).

Domain and Range Calculator, Practice Problems, and Answers

Community Q&A
You Might Also Like

- ↑ http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U17_L2_T3_text_final.html
- ↑ https://www.cuemath.com/calculus/domain-and-range-of-a-function/
- ↑ http://www.biology.arizona.edu/biomath/tutorials/notation/setbuildernotation.html
- ↑ https://www.khanacademy.org/math/algebra-home/alg-functions/alg-determining-the-range-of-a-function/a/finding-range-of-quadratic-functions
- ↑ https://math.libretexts.org/Courses/Borough_of_Manhattan_Community_College/MAT_206_Precalculus/3%3A_Polynomial_and_Rational_Functions_New/3.2%3A_Quadratic_Functions
About This Article

The domain of a function is the collection of independent variables of x, and the range is the collection of dependent variables of y. To find the domain of a function, just plug the x-values into the quadratic formula to get the y-output. To find the range of a function, first find the x-value and y-value of the vertex using the formula x = -b/2a. Then, plug that answer into the function to find the range. To properly notate the range, write out the numbers in brackets if they're included in the domain or in parenthesis if they're not included in the domain. To learn how to find the range of a function graphically, read on! Did this summary help you? Yes No
- Send fan mail to authors
Reader Success Stories
Dec 1, 2023
Did this article help you?

Featured Articles

Trending Articles

Watch Articles

- Terms of Use
- Privacy Policy
- Do Not Sell or Share My Info
- Not Selling Info
Don’t miss out! Sign up for
wikiHow’s newsletter

- Mathematicians
- Math Lessons
- Square Roots
- Math Calculators
- Domain and Range of a Function – Explanation & Examples
JUMP TO TOPIC
History of a function
Here are a few examples of the application of a function., how to use interval notations to specify domain and range, how to find the domain for a function with no denominator or radicals, how to find the domain for a rational function with a variable in the denominator, how to the domain for a function with a variable inside a radical sign, how to find the domain of a function using the natural logarithm (ln), how to find the domain and range of a relation, practice questions, domain and range of a function – explanation & examples.

In mathematics, we can compare a function to a machine that generates some output in correlation to a given input . By taking an example of a coin stamping machine, we can illustrate a function’s meaning as follows.
When you insert a coin into the coin stamping machine, the result is a stamped and flattened piece of metal. By considering a function, we can relate the coin and the flattened piece of metal with the domain and range. In this case, a function is considered to be the coin stamping machine.
Just like the coin stamping machine, which can only produce a single flattened piece of metal at a time, a function works in the same manner by giving out one result at a time.
The idea of a function was introduced in the early seventeenth century when Rene Descartes ( 1596-1650 ) used the concept in his book Geometry (1637) to model mathematical problems.
Fifty years later, after the publication of Geometry, Gottfried Wilhelm Leibniz (1646-1716) introduced the term “function.” Later, Leonhard Euler (1707-1783) played a big role by introducing the technique of function notion, y = f (x).
Real-life application of a function
Functions are very useful in mathematics because they allow us to model real-life problems into a mathematical format.
Circumference of a circle
The circumference of a circle is a function of its diameter or radius. We can mathematically represent this statement as:
C(d) =dπ or C(r)=2π⋅r
The length of the shadow of an object is a function of its height.
The position of a moving object
The location of a moving object such as a car is a function of time.
Temperature
The temperature of a body is based on several factors and inputs.
The compound or simple interest is a function of the time, principal, and interest rate.
Height of an object
The height of an object is a function of his/her age and body weight.
Having learned about a function now can proceed to how to calculate the domain and the range of a function.
What is the Domain and Range of a Function?
The domain of a function is the input numbers that, when plugged into a function, the result is defined. In simple words, we can define the domain of a function as the possible values of x that will make an equation true.
Some of the instances that will not make a valid function are when an equation is being divided by zero or a negative square root.
For example, f( x ) = x 2 is a valid function because, no matter what value of x can be substituted into an equation, there is always a valid answer. For this reason, we can conclude that the domain of any function is all real numbers.
The range of a function is defined as a set of solutions to the equation for a given input. In other words, the range is the output or y value of a function. There is only one range for a given function.
Since the range and domain of a function are usually expressed in interval notation, it’s important to discuss the concept of interval notation.
The procedure for doing interval notation include:
- Write the numbers separated by a comma in ascending order.
- Enclose the numbers using parentheses () to show that an endpoint value is not included.

How to Find the Domain and Range of a Function?
We can determine the domain of a function either algebraically or by the graphical method. To calculate the domain of a function algebraically, you solve the equation to determine the values of x.
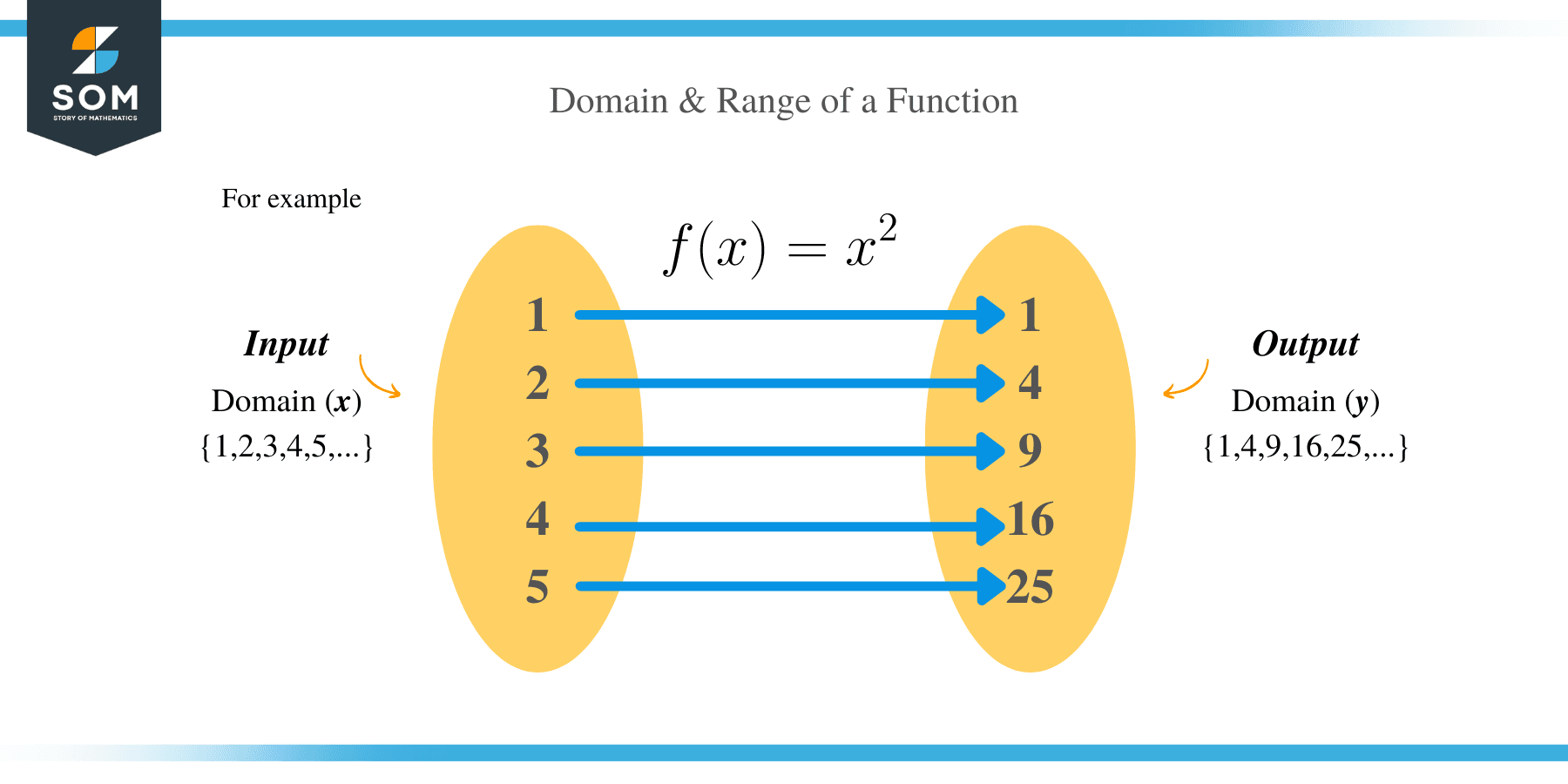
Let’s examine these types of functions and how to calculate their domain.
Let’s see a few examples below to understand this scenario.
Find the domain of f (x) = 5x − 3
The domain of a linear function is all real numbers, therefore,
Domain: (−∞, ∞)
Range: (−∞, ∞)
A function with a radical
Find the domain of the function f(x)=−2x 2 + 12x + 5
The function f(x) = −2x 2 + 12x + 5 is a quadratic polynomial, therefore, the domain is (−∞, ∞)
To find the domain of this type of function, set the denominator to zero and calculate the variable’s value.
Determine the domain of x−4/ (x 2 −2x−15)
Set the denominator to zero and solve for x
⟹ x 2 − 2x – 15 = (x − 5) (x + 3) = 0
Hence, x = −3, x = 5
For the denominator not to be zero, we need to avoid the numbers −3 and 5. Therefore, the domain is all real numbers except −3 and 5.
Calculate the domain and the range of the function f(x) = -2/x.
Set the denominator to zero.
Therefore, domain: All real numbers except 0.
The range is all real values of x except 0.
Find the domain and range of the following function.
f(x) = 2/ (x + 1)
Set the denominator equal to zero and solve for x.
Since the function is undefined when x = -1, the domain is all real numbers except -1. Similarly, the range is all real numbers except 0
To find the domain of the function, the terms inside the radical are set the inequality of > 0 or ≥ 0. Then, the value of the variable is determined.
Find the domain of f(x) = √ (6 + x – x 2 )
To avoid the square roots of negative numbers, we set the expression inside the radical sign to ≥ 0.
6 + x – x 2 ≥ 0 ⟹ x 2 – x – 6≤ 0
⟹ x 2 – x – 6= (x – 3) (x +2) = 0
Therefore, the function is zero if x = 3 or x = -2
Hence the domain: [−2, 3]
Find the domain of f(x) =x/√ (x 2 – 9)
Set the expression within the radical sign to x 2 – 9 > 0 Solve for the variable to get;
x = 3 or – 3
Therefore, Domain: (−∞, −3) & (3, ∞)
Find the domain of f(x) = 1/√ (x 2 -4)
By factoring the denominator, we get x ≠ (2, – 2).
Test your answer by plugging -3 into the expression within the radical sign.
⟹ (-3) 2 – 4 = 5
also try with zero
⟹ 0 2 – 4 = -4, therefore number between 2 and -2 are invalid
Try number above 2
⟹ 3 2 – 4 = 5. This one is valid.
Hence, the domain = (-∞, -2) U (2, ∞)
To find the domain of a function using natural log, set the terms within the parentheses to >0 and then solve.
Let’s see an example below to understand this scenario.
Find the domain of the function f(x) = ln (x – 8)
⟹ x – 8 > 0
⟹ x – 8 + 8 > 0 + 8
Domain:(8, ∞)
A relation is an asset of x and y coordinates. To find the domain and range in a relation, just list the x and y values, respectively.
State the domain and range of the relation {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}
List the x values. Domain: {2, 3, 4, 6}
List the y values. range: {–3, –1, 3, 6}
Find the domain and range of the relation {(–3, 5), (–2, 5), (–1, 5), (0, 5), (1, 5), (2, 5)}
The domain is {–3, –2, –1, 0, 1, 2} and the range is {5}
Given that R = {(4, 2) (4, -2), (9, 3) (9, -3)}, find the domain and range of R.
The domain is a list of first values, therefore, D= {4, 9} and the range = {2, -2, 3, -3}
Previous Lesson | Main Page | Next Lesson
Domain and Range
Functions in mathematics can be compared to the operations of a vending (soda) machine. When you put in a certain amount of money, you can select different types of sodas. Similarly, for functions, we input different numbers and we get new numbers as the result. Domain and range are the main aspects of functions.
- You can use quarters and one-dollar bills to buy a soda. The machine will not give you any flavor of the soda if pennies are input. Hence, the domain represents the inputs we can have here, that is, quarters and one-dollar bills.
- No matter what amount you pay, you won't get a cheeseburger from a soda machine. Thus, the range is the possible outputs we can have here, that is, the flavors of soda in the machine.
Let us learn to find the domain and range of a function, and also graph them.
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. | |
| 7. | |
| 8. | |
| 9. | |
| 10. | |
| 11. |
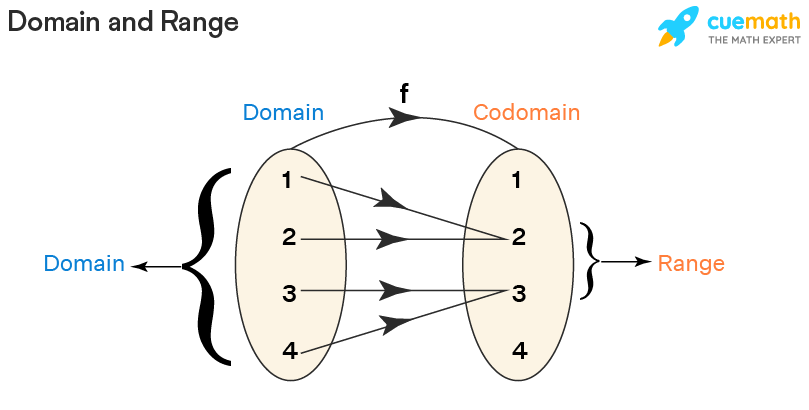
What is Domain and Range?
The domain and range of a relation are the sets of all the x-coordinates and all the y-coordinates of ordered pairs respectively. For example, if the relation is, R = {(1, 2), (2, 2), (3, 3), (4, 3)}, then:
- Domain = the set of all x-coordinates = {1, 2, 3, 4}
- Range = the set of all y-coordinates = {2, 3}
We can visualize this here:
The concept of domain and range is further implemented for functions as well.
Domain and Range of a Function
The domain and range of a function are the components of a function . The domain is the set of all the input values of a function and the range is the possible output given by the function. Domain→ Function →Range. If there exists a function f: A →B such that every element of set A is mapped to elements in set B, then A is the domain and B is the co-domain. The image of an element 'a' under a relation R is given by 'b', where (a,b) ∈ R. The range of the function is the set of images. The domain and range of a function are denoted in general as follows: Domain(f) = {x ∈ R : Condition} and range(f)={f(x) : x ∈ domain(f)}
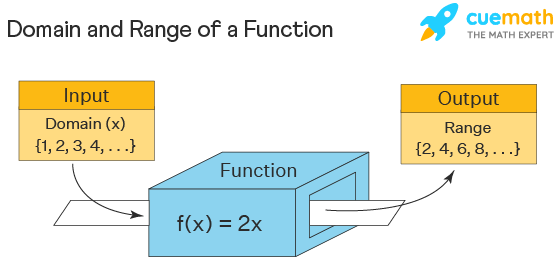
The domain and range of this function f(x) = 2x is given as domain D = {x ∈ N} , range R = {y ∈ N: y = 2x}
Domain of a Function
A domain of a function refers to "all the values" that can go into a function without resulting in undefined values. i.e., The domain in math is the set of all possible inputs for the function. Consider the above box as a function f(x) = 2x . Inputting the values x = {1,2,3,4,...}, the domain is simply the set of natural numbers. But in general (if the domain is not specified as natural numbers), f(x) = 2x is defined for all real values of x and hence its domain is the set of all real numbers which is denoted by (-∞, ∞). Here are the general formulas used to find the domain of different types of functions. Here, R is the set of all real numbers.
Rules of Finding Domain of a Function
- Domain of any polynomial (linear, quadratic, cubic, etc) function is ℝ (all real numbers).
- Domain of a square root function √x is x ≥ 0.
- Domain of an exponential function is ℝ.
- Domain of logarithmic function is x>0.
- To find the domain of a rational function y = f(x), set the denominator ≠ 0.
How to Find Domain of a Function?
To find the domain of a function, we simply apply one of the above-mentioned rules of finding domain depending on the type of the function. Here are some examples:
Example 1: To find the domain of a function f(x) = √(x + 3), we apply the rule 2 mentioned above. Then we get: x + 2 ≥ 0. Solving this inequality , we get x ≥ -2. Thus, the domain of f(x) is [-2, ∞).
Example 2: To calculate the domain of a function g(x) = (2x + 1) / (x - 2), we apply the rule 5 mentioned above. Then we get x - 2 ≠ 0. Solving this, we get x ≠ 2. Thus, its domain is the set of all real numbers except 2 which in interval notation can be written as (-∞, 2) ∪ (2, ∞).
Range of a Function
The range of a function is the set of all its outputs. Example: Let us consider the function f: A→ B, where f(x) = 2x and each of A and B = {set of natural numbers }. Here we say A is the domain and B is the co-domain. Then the output of this function becomes the range. The range = {set of even natural numbers}. The elements of the domain are called pre-images and the elements of the co-domain which are mapped are called the images. Here, the range of the function f is the set of all images of the elements of the domain (or) the set of all the outputs of the function.
Rules of Finding Range of a Function
The best way to determine the range of a function is by graphing it and looking at the y-value that the graph covers. But here are the general rules used to find the range of some popular functions. Note that ℝ is the set of all real numbers here.
- Range of a linear function is ℝ.
- Range of a quadratic function y = a(x - h) 2 + k is: y ≥ k, if a > 0 and y ≤ k, if a < 0
- Range of a square root function is y ≥ 0.
- Range of an exponential function is y > 0.
- Range of logarithmic function is ℝ.
- To find the range of a rational function y = f(x), solve it for x and set the denominator ≠ 0.
How to Find Range of a Function?
If a function is present in one of the functions mentioned in the above rules, we can straight away apply the rules and find its range. Otherwise, we can graph it and look at the y-values the graph covers to calculate range. Here are some examples:
Example 1: To calculate the range of the function f(x) = 2 (x - 3) 2 - 5, apply rule 1 mentioned above. Then its range is y ≥ -5 (or) [-5, ∞).
Example 2: To find the range of a function g(x) = ln (2x - 3) + 4, we apply the rule 4. Then we get its range to be the set of all real numbers (ℝ).
How To Calculate Domain And Range?
Suppose X = {1, 2, 3, 4, 5} and Y = {1, 2, 3, 4, 5, 6}. Consider the function f: X → Y, where R = {(x,y) : y = x+1}.
- Domain = the input values. Thus Domain = X = {1, 2, 3, 4, 5}
- Range = the output values of the function = {1 + 1, 2 + 1, 3 + 1, 4 + 1, 5 + 1} = {2, 3, 4, 5, 6}
Note that Y is the codomain here but NOT range.
Let's understand the domain and range of some special functions taking different types of functions into consideration.
Domain and Range of Exponential Functions
The function y = a x , a ≥ 0 is defined for all real numbers. Hence, the domain of the exponential function is the entire real line. The exponential function always results in a positive value. Thus, the range of the exponential function is of the form y= a x is {y ∈ ℝ: y > 0}. Therefore, Domain = ℝ, Range = (0, ∞)
Example: Look at the graph of this function f: 2 x
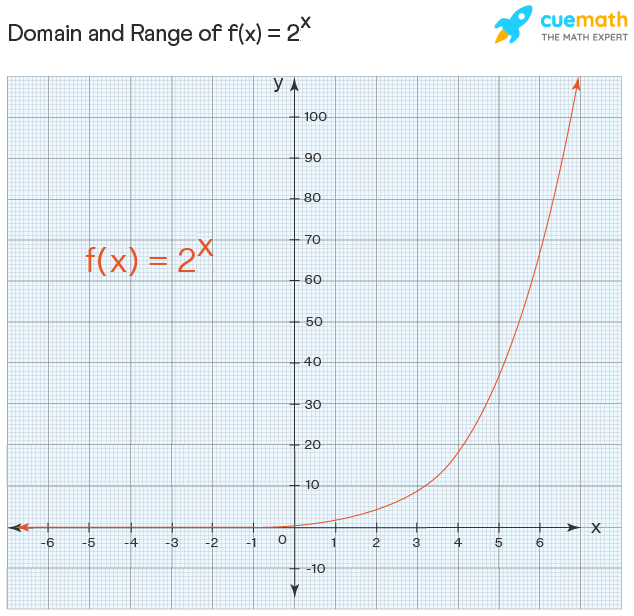
Observe that the value of the function is closer to 0 as x tends to ∞ but it will never attain the value 0. The domain and range of exponential functions are given as follows:
- Domain: The domain of the function is the set ℝ.
- Range: The exponential function always results in positive real values.
Domain and Range of Trigonometric Functions
Look at the graph of the sine function and cosine function . Notice that the value of the functions oscillates between -1 and 1 and it is defined for all real numbers.
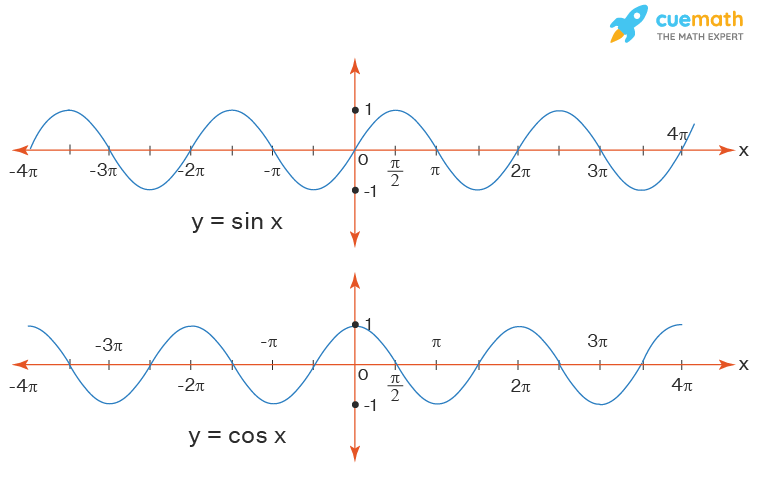
Thus, for each of the sine and cosine functions:
- Domain: The domain of the functions is the set ℝ (or) (-∞, + ∞).
- Range: The range of the functions is [-1, 1]
The domain and range of all trigonometric functions are shown below:
| sin θ | (-∞, + ∞) | [-1, +1] |
| cos θ | (-∞ +∞) | [-1, +1] |
| tan θ | ℝ - (2n + 1)π/2 | (-∞, +∞) |
| cot θ | ℝ - nπ | (-∞, +∞) |
| sec θ | ℝ - (2n + 1)π/2 | (-∞, -1] U [+1, +∞) |
| cosec θ | ℝ - nπ | (-∞, -1] U [+1, +∞) |
Domain and Range of an Absolute Value Function
The function y = |ax + b| is defined for all real numbers. So, the domain of the absolute value function is the set of all real numbers. The absolute value of a number always results in a non-negative value. Thus, the range of an absolute value function of the form y= |ax+b| is {y ∈ ℝ | y ≥ 0}. The domain and range of an absolute value function are given as follows
- Range = [0, ∞)
Example: Find the domain and range of the function f(x) = |6 - x|.
- Range: Its range is [0, ∞)
Domain and Range of a Square Root Function
A square root function is of the form f(x) = √(ax+b). We know that the square root of a negative number is not defined. So the function y= √(ax+b) is defined only when ax + b ≥ 0. When we solve this for x, we get x ≥ -b/a.
So, the domain of the square root function is the set of all real numbers greater than or equal to -b/a. We know that the square root of something always results in a non-negative value. Thus, the range of a square root function is the set of all non-negative real numbers. Hence, the domain and range of a square root function are given as: Domain = [-b/a,∞), Range = [0,∞)
Example: Calculate the domain and range of the function h(x) = 2- √(-3x+2).
Domain: A square root function is defined only when the value inside it is a non-negative number. So for a domain,
Range: We already know that the square root function results in a non-negative value always.
√(-3x+2) ≥ 0
Multiply -1 on both sides
-√(-3x+2) ≤ 0
Adding 2 on both sides
2-√(-3x+2) ≤ 2
Thus, the domain of h(x) = (-∞, 2/3] and range of h(x) = (-∞, 2].
Domain and Range From Graph
It is very easy to find the domain and range of a graph. The set of values of x covered by the graph gives the domain and the set of values of y covered by the graph gives the range. But keep a note of the following things while writing the domain and range from a graph.
- See whether the graph passes the vertical line test . Otherwise, it is not a function and we do not usually define domain and range for such curves.
- If there is any hole on the graph, then its coordinates shouldn't be in the domain and range.
- If there is a vertical asymptote , then the corresponding value of x shouldn't be there in the domain.
- If there is a horizontal asymptote , then the corresponding value of x shouldn't be there in the range.
- If the graph is broken into pieces , then we get multiple sets/intervals in the domain and range and we club all such sets/intervals by " union " symbol (∪).
- If there is an arrow at the end of a curve, then it means that the curve is supposed to be extended infinitely in that particular direction.
Here is an example of a graph and we will find the domain and range of the graph.
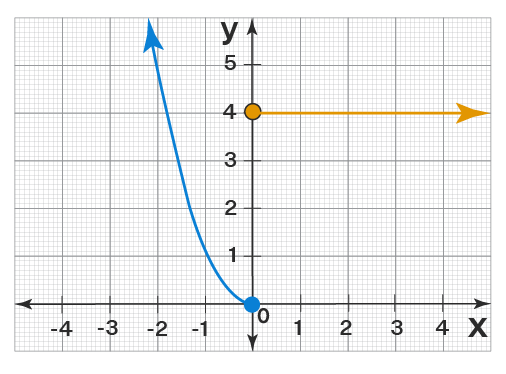
In the above graph:
- All the x-values from -∞ to ∞ are covered by the graph (because of arrows, the two curves extend infinitely in the given directions). Hence, the domain = (-∞, ∞).
- All the y-values greater than or equal than or equal to 0 are covered by the graph (see there is no part of the curve that is below the y-axis). Hence, the range = [0, ∞).
Example 2: Using the same process mentioned above, the domain of the graph below is [-5, ∞) and its range from graph is (-∞, 5].
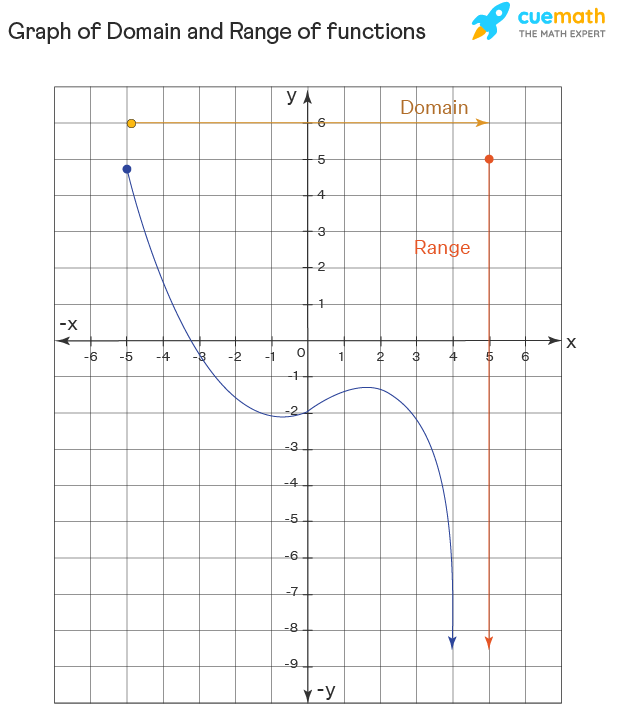
Important Notes on Domain and Range:
- The domain and range of a function is the set of all possible inputs and outputs of a function respectively.
- To find the domain of a function f(x), think for what values of x it is defined.
- To calculate the range of a function f(x), think of what y values it will produce. The most easiest way to find the range of a function is to graph it.
☛ Related Topics:
- Graphing Functions
- Cubic Functions
- Inverse Trigonometric Functions
Examples on Domain and Range
Example 1. Find the domain and range of the real function f defined by f(x) = √(x - 1)
Given the function is real. Thus the domain and range of the function are also real.
| x | Real Number(Yes/No) | |
|---|---|---|
| 2 | √(2-1) = 1 | Yes |
| 1 | √(1-1) =0 | Yes |
| 0 | √(0-1) =√-1 | No |
| -1 | √(-1-1) = √-2 | No |
| -2 | √(-2-1) = √-3 | No |
The minimum value it could take is 1 and the maximum value is ∞. Thus domain = [1, ∞).
Since f(x) is always non-negative, the minimum value of the range is 0 and it can range up to infinity. Thus range = [0, ∞)
Using the rules of finding domain, the domain of f(x) is obtained by solving x - 1 ≥ 0. Then we get x ≥ 1. Thus, the domain is [1, ∞).
Range of a square root is always the set of all non-negative numbers. Thus, the range is [0, ∞).
Answer: The domain and the range of the function f defined by f(x) = √(x - 1) is domain = [1, ∞) and range = [0, ∞)
Example 2: We define a function f: R - {0} → R as f(x)=1/x. Complete the table shown below. Find the domain and range of the function.
| x | -2 | -1.5 | -1 | -0.5 | 0.25 | 0.5 | 1 | 1.5 | 2 |
|---|---|---|---|---|---|---|---|---|---|
Let's complete the given table by finding the values of the function at the given values x. Plugging in the values of x in the given function, we find the range of f(x) = 1/x.
| x | |
|---|---|
| -2 | 0.5 |
| -1.5 | -0.67 |
| -1 | -1 |
| -0.5 | -2 |
| 0.25 | 4 |
| 0.5 | 2 |
| 1 | 1 |
| 1.5 | 0.67 |
| 2 | 0.5 |
Let's draw the graph of the function to determine the domain and range of the function.
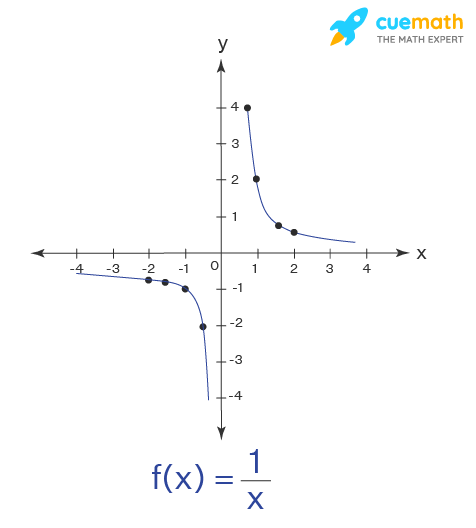
From the graph, we can observe that the domain and range of the function are all real numbers except 0.
Answer: So, the domain and range of f(x) = 1/x is R - {0} (or) (-∞,0) ∪ (0, ∞).
Example 3: Find the domain and range of the function y = (x + 1)/(3 - x).
A rational function is defined only when its denominator is NOT 0.
Thus, we will set the denominator NOT equal to 0, and then we will solve for x.
- x ≠ - 3 ⇒ x ≠ 3
So, the domain is the set of real numbers x except 3, i.e., domain = (-∞, 3) ∪ (3, ∞).
Let's find the range of y = (x + 1)/(3 - x)
Let us solve the given equation for x
(3 - x)y = x + 1
3y - xy = x + 1
3y-1 = x + xy
x(1 + y) = 3y - 1
x = (3y - 1)/(1 + y)
The final equation is a fraction and a fraction is NOT defined when its denominator is zero.
So 1 + y ≠ 0 ⇒ y ≠ -1
Therefore, the range of the given function is the set of all real numbers excluding -1. i.e., the range = (- ∞ ,-1) ∪ (-1, ∞ ).
Answer: Domain = (-∞, 3) ∪ (3, ∞), Range = (-∞,-1) ∪ (-1, ∞)
go to slide go to slide go to slide

Book a Free Trial Class
Practice Questions on Domain and Range
go to slide go to slide
FAQs on Domain and Range
What is the domain and range of a function.
The domain and range of a function are the set of all the inputs and outputs a function can give respectively. i.e., for any function y = f(x):
- the domain is the set of all x-values for which f(x) is defined.
- the range is the set of all y-values that the function f(x) produce.
How Do You Write the Domain and Range?
We write the domain and range of a function as the set of all the inputs a function can take and the outputs of the functions respectively. Since these are nothing but sets, we can write them either in roaster form or set builder notation . The domain and range in the interval notation involve open and square brackets.
How to Find Domain and Range of a Graph?
The domain from a graph is the set of all x-values the graph covers and the range of a graph is the set of all y-values that it covers.
What is The Domain and Range of a Constant Function?
Let the constant function be f(x) = k. The domain of a constant function is given by ℝ, that is, the set of real numbers. The range of a constant function is given by the singleton set , {k}. The domain and range of a constant function is given as domain = ℝ and range = {k}, which is a singleton set.
What is the Definition of Domain in Math?
The domain in math is usually defined for relations/functions. The domain of a function is the set of all values that are possible to input into it. For example, for the function f(x) = √x, it is possible to input only non-negative values into it. Thus, its domain is the set of all non-negative real numbers.
How to Find the Domain of a Function which is Rational?
To find the domain of a rational function , we just set the denominator not equal to zero. For example, to find the domain of f(x) = 2/(x-3), we set x-3 ≠ 0, by solving this, we get x≠3. So the domain is the set of all rational numbers except 3. This can be written in the interval notation as (-∞, 3) U (3, ∞).
What are the Rules to Find the Domain of a Function?
Here are some general rules used to find domain of different types of functions:
- f(x) = polynomial , the domain is the set of all real numbers.
- f(x) = 1/x, domain if the set of all real numbers but x≠0.
- f(x) = √x, domain if the set of all real numbers such that x ≥ 0.
- f(x) = ln x, domain is the set of all real numbers such that x > 0.
How to Find Domain and Range of Function?
To find the domain of a function y = f(x), we need to look for set of all possible values of x that does not make the function undefined. The common examples include dividing by 0, taking the square root of negative numbers, etc. To calculate the range of a function, imagine what y-values the function produces. When imagination is not possible, graph the function and take a look at the y-values that the graph covers.
How to Find Range of a Rational Function?
To find the range of a rational function, we just solve the equation for x and set the denominator not equal to zero. For example, to find the range of y=2/(x-3), solve it for x first. Then we get, x-3 = 2/y and from this, x = (2/y) + 3. Then its range is y≠0 (or) in interval notation, (-∞, 0) U (0, ∞).
How to Find Domain and Range of an Equation?
To find the domain and range of an equation y = f(x), determine the values of the independent variable x for which the function is defined. To calculate the range of the function, we simply express the equation as x = g(y) and then find the domain of g(y).
How to Calculate the Domain and Range From the Graph of a Function?
The set of all x-coordinates of all points of the curve would give the domain and the set of all y-coordinates of all points of the curve would give the range. Each of domain and range can be either written as a set or an interval.
What is The Difference Between Domain and Range of a Function?
Domain and Range of a function are the components of a function. The domain of a function is the set of all possible inputs for the function, whereas the range of function is the set of all the outputs a function can give.
What is The Domain and Range of a Relation?
The domain and range of a relation is found as follows. Let R be the relation from a non-empty set A to a non-empty set B. The domain and range of the relation are the set of first elements and the second elements respectively in the ordered pairs in relation R is called the domain.
What is the Domain and Range of Composite Functions?
Let the composite function be h(x) = (f ∘ g)(x). The domain and range of h are determined as follows. The domain of h is either same as f or lies within the domain of f. The range h must lie within the range of g. Let f(x) = x 2 and g(x) = x+ 3. We know that g: X →Y and f: Y →Z. Then fog: X →Z. f(g(x)) = (x+3) 2 . Thus the domain and range are: domain= {All the elements in set X}, range= {all the elements in set Z}
What is the Domain and Range of a Quadratic Function?
The domain and range of a quadratic function y = a(x - h) 2 + k determine the nature of the parabola : whether it is upwards or downwards.
- y ≥ k, if the function has a minimum value, that is, when a > 0 (parabola opens up)
- y ≤ k, if the function has a maximum value, that is, when a < 0 (parabola opens down)
How to Find the Range of a Graph?
The y-axis is responsible for range. Thus, to find the range of a graph look at the y-values covered by the graph. The highest and lowest values of the graphs are helpful in writing the range of a graph.
Domain and range
The domain and range of a function is all the possible values of the independent variable, x , for which y is defined. The range of a function is all the possible values of the dependent variable y . In other words, the domain is the set of values that we can plug into a function that will result in a real y-value; the range is the set of values that the function takes on as a result of plugging in an x value within the domain of the function.
In mathematical terms, given a function f(x), the values that f(x) can take on constitute the range of the function, while all the possible x values constitute the domain. Consider the function f(x) = x 2 .
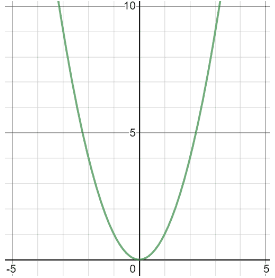
There are no x-values that will result in the function being undefined and matter what real x-value we plug in, the result will always be a real y-value. Thus, the domain of f(x) = x 2 is all x-values. Then, from looking at the graph or testing a few x-values, we can see that any x-value we plug in will result in a positive y-value. Thus, the range of f(x) = x 2 is all positive y-values.
Notice in the examples above that we described the domain and range using words. While this is possible for all functions, different notations have been developed for expressing domains and ranges in a more concise way. This makes it far easier to express the domains and ranges of multiple functions at a time, particularly as functions get more complicated. Two of these notations are interval notation and set notation.
Interval notation
When using interval notation, domain and range are written as intervals of values. The table below shows the basic symbols used in interval notation and what they mean:
| Name | Symbol | Meaning |
|---|---|---|
| Parentheses | ( ) | Endpoints not included (exclusive) |
| Brackets | [ ] | Endpoints included (inclusive) |
| Union | ∪ | "or" - used to combine two or more sets |
When indicating the domain in interval notation, we need to keep the following in mind:
- The smallest term in the interval is written first, followed by a comma, and then the largest term.
- The first term is the left endpoint and the second term is the right endpoint.
- The endpoints are written between either parentheses or brackets, depending on whether the endpoint is included or not.
Let's look at the same example as above, f(x) = x 2 to see how interval notation is used. Recall that the domain of f(x) = x 2 is all real numbers. In other words, any value from negative infinity to positive infinity will yield a real result. Thus, we can write the domain as:
(-∞, ∞)
We used parentheses rather than brackets around each endpoint because the endpoints are negative and positive infinity, which by definition have no bound. Recall that the range of f(x) = x 2 is all positive y-values, including 0. The range can therefore be written in interval notation as:
[0, ∞)
The union symbol is used when we have a function whose domain or range cannot be described with just a single interval. The union symbol can be read as "or" and it is used throughout various fields of mathematics. In the context of interval notation, it simply means to combine two given intervals. For example, consider the function:
This is the same as our function above, except that it is not defined over the interval (0, 1). The domain of the function is therefore all x-values except those in the interval (0, 1), which we can indicate in interval notation using the union symbol as follows:
(-∞, 0] ∪ [1, ∞)
Note that it is also possible to use multiple union symbols to combine more intervals in the same manner.
Set notation
When using set notation, also referred to as set builder notation, we use inequality symbols to describe the domain and range as a set of values. Like interval notation, there are a number of symbols used in set notation, the most common of which are shown in the table below:
| Name | Symbol | Meaning |
|---|---|---|
| Braces | { } | "the set of" - indicates a set |
| Vertical bar | | | "such that" - symbol is followed by a constraint |
| "Element of" | ∈ | Indicates that an element is a member of some set |
| Double-struck R | ℝ | The set of all real numbers |
| Union | ∪ | "or" - used to combine two or more sets |
Standard inequality symbols such as , ≥, and so on are also used in set notation.
Using the same example as above, the domain of f(x) = x 2 in set notation is:
{x | x∈ℝ}
The above can be read as "the set of all x such that x is an element of the set of all real numbers." In other words, the domain is all real numbers. We could also write the domain as {x | -∞ < x < ∞}.
The range of f(x) = x 2 in set notation is:
{y | y ≥ 0}
which can be read as "the set of all y such that y is greater than or equal to zero."
Like interval notation, we can also use unions in set builder notation. However, in set notation, rather than using the symbol "∪," we use the word "or" by convention. For example example, given the function
we can write the domain of the above function in set notation as:
{x | x ≤ 0 or x ≥ 1}
3.2 Domain and Range
Learning objectives.
In this section, you will:
- Find the domain of a function defined by an equation.
- Graph piecewise-defined functions.
Horror and thriller movies are both popular and, very often, extremely profitable. When big-budget actors, shooting locations, and special effects are included, however, studios count on even more viewership to be successful. Consider five major thriller/horror entries from the early 2000s— I am Legend , Hannibal , The Ring , The Grudge , and The Conjuring . Figure 1 shows the amount, in dollars, each of those movies grossed when they were released as well as the ticket sales for horror movies in general by year. Notice that we can use the data to create a function of the amount each movie earned or the total ticket sales for all horror movies by year. In creating various functions using the data, we can identify different independent and dependent variables, and we can analyze the data and the functions to determine the domain and range. In this section, we will investigate methods for determining the domain and range of functions such as these.
Finding the Domain of a Function Defined by an Equation
In Functions and Function Notation , we were introduced to the concepts of domain and range . In this section, we will practice determining domains and ranges for specific functions. Keep in mind that, in determining domains and ranges, we need to consider what is physically possible or meaningful in real-world examples, such as tickets sales and year in the horror movie example above. We also need to consider what is mathematically permitted. For example, we cannot include any input value that leads us to take an even root of a negative number if the domain and range consist of real numbers. Or in a function expressed as a formula, we cannot include any input value in the domain that would lead us to divide by 0.
We can visualize the domain as a “holding area” that contains “raw materials” for a “function machine” and the range as another “holding area” for the machine’s products. See Figure 2 .
We can write the domain and range in interval notation , which uses values within brackets to describe a set of numbers. In interval notation, we use a square bracket [ when the set includes the endpoint and a parenthesis ( to indicate that the endpoint is either not included or the interval is unbounded. For example, if a person has $100 to spend, they would need to express the interval that is more than 0 and less than or equal to 100 and write ( 0 , 100 ] . ( 0 , 100 ] . We will discuss interval notation in greater detail later.
Let’s turn our attention to finding the domain of a function whose equation is provided. Oftentimes, finding the domain of such functions involves remembering three different forms. First, if the function has no denominator or an odd root, consider whether the domain could be all real numbers. Second, if there is a denominator in the function’s equation, exclude values in the domain that force the denominator to be zero. Third, if there is an even root, consider excluding values that would make the radicand negative.
Before we begin, let us review the conventions of interval notation:
- The smallest number from the interval is written first.
- The largest number in the interval is written second, following a comma.
- Parentheses, ( or ), are used to signify that an endpoint value is not included, called exclusive.
- Brackets, [ or ], are used to indicate that an endpoint value is included, called inclusive.
See Figure 3 for a summary of interval notation.
Finding the Domain of a Function as a Set of Ordered Pairs
Find the domain of the following function: { ( 2 , 10 ) , ( 3 , 10 ) , ( 4 , 20 ) , ( 5 , 30 ) , ( 6 , 40 ) } { ( 2 , 10 ) , ( 3 , 10 ) , ( 4 , 20 ) , ( 5 , 30 ) , ( 6 , 40 ) } .
First identify the input values. The input value is the first coordinate in an ordered pair . There are no restrictions, as the ordered pairs are simply listed. The domain is the set of the first coordinates of the ordered pairs.
Find the domain of the function:
{ ( −5 , 4 ) , ( 0 , 0 ) , ( 5 , −4 ) , ( 10 , −8 ) , ( 15 , −12 ) } { ( −5 , 4 ) , ( 0 , 0 ) , ( 5 , −4 ) , ( 10 , −8 ) , ( 15 , −12 ) }
Given a function written in equation form, find the domain.
- Identify the input values.
- Identify any restrictions on the input and exclude those values from the domain.
- Write the domain in interval form, if possible.
Finding the Domain of a Function
Find the domain of the function f ( x ) = x 2 − 1. f ( x ) = x 2 − 1.
The input value, shown by the variable x x in the equation, is squared and then the result is lowered by one. Any real number may be squared and then be lowered by one, so there are no restrictions on the domain of this function. The domain is the set of real numbers.
In interval form, the domain of f f is ( − ∞ , ∞ ) . ( − ∞ , ∞ ) .
Find the domain of the function: f ( x ) = 5 − x + x 3 . f ( x ) = 5 − x + x 3 .
Given a function written in an equation form that includes a fraction, find the domain.
- Identify any restrictions on the input. If there is a denominator in the function’s formula, set the denominator equal to zero and solve for x x . If the function’s formula contains an even root, set the radicand greater than or equal to 0, and then solve.
- Write the domain in interval form, making sure to exclude any restricted values from the domain.
Finding the Domain of a Function Involving a Denominator
Find the domain of the function f ( x ) = x + 1 2 − x . f ( x ) = x + 1 2 − x .
When there is a denominator, we want to include only values of the input that do not force the denominator to be zero. So, we will set the denominator equal to 0 and solve for x . x .
Now, we will exclude 2 from the domain. The answers are all real numbers where x < 2 x < 2 or x > 2 x > 2 as shown in Figure 4 . We can use a symbol known as the union, ∪ , ∪ , to combine the two sets. In interval notation, we write the solution: ( −∞ , 2 ) ∪ ( 2 , ∞ ) . ( −∞ , 2 ) ∪ ( 2 , ∞ ) .
Find the domain of the function: f ( x ) = 1 + 4 x 2 x − 1 . f ( x ) = 1 + 4 x 2 x − 1 .
Given a function written in equation form including an even root, find the domain.
- Since there is an even root, exclude any real numbers that result in a negative number in the radicand. Set the radicand greater than or equal to zero and solve for x . x .
- The solution(s) are the domain of the function. If possible, write the answer in interval form.
Finding the Domain of a Function with an Even Root
Find the domain of the function f ( x ) = 7 − x . f ( x ) = 7 − x .
When there is an even root in the formula, we exclude any real numbers that result in a negative number in the radicand.
Set the radicand greater than or equal to zero and solve for x . x .
Now, we will exclude any number greater than 7 from the domain. The answers are all real numbers less than or equal to 7 , 7 , or ( − ∞ , 7 ] . ( − ∞ , 7 ] .
Find the domain of the function f ( x ) = 5 + 2 x . f ( x ) = 5 + 2 x .
Can there be functions in which the domain and range do not intersect at all?
Yes. For example, the function f ( x ) = − 1 x f ( x ) = − 1 x has the set of all positive real numbers as its domain but the set of all negative real numbers as its range. As a more extreme example, a function’s inputs and outputs can be completely different categories (for example, names of weekdays as inputs and numbers as outputs, as on an attendance chart), in such cases the domain and range have no elements in common.
Using Notations to Specify Domain and Range
In the previous examples, we used inequalities and lists to describe the domain of functions. We can also use inequalities, or other statements that might define sets of values or data, to describe the behavior of the variable in set-builder notation . For example, { x | 10 ≤ x < 30 } { x | 10 ≤ x < 30 } describes the behavior of x x in set-builder notation. The braces { } { } are read as “the set of,” and the vertical bar | is read as “such that,” so we would read { x | 10 ≤ x < 30 } { x | 10 ≤ x < 30 } as “the set of x -values such that 10 is less than or equal to x , x , and x x is less than 30.”
Figure 5 compares inequality notation, set-builder notation, and interval notation.
To combine two intervals using inequality notation or set-builder notation, we use the word “or.” As we saw in earlier examples, we use the union symbol, ∪ , ∪ , to combine two unconnected intervals. For example, the union of the sets { 2 , 3 , 5 } { 2 , 3 , 5 } and { 4 , 6 } { 4 , 6 } is the set { 2 , 3 , 4 , 5 , 6 } . { 2 , 3 , 4 , 5 , 6 } . It is the set of all elements that belong to one or the other (or both) of the original two sets. For sets with a finite number of elements like these, the elements do not have to be listed in ascending order of numerical value. If the original two sets have some elements in common, those elements should be listed only once in the union set. For sets of real numbers on intervals, another example of a union is
Set-Builder Notation and Interval Notation
Set-builder notation is a method of specifying a set of elements that satisfy a certain condition. It takes the form { x | statement about x } { x | statement about x } which is read as, “the set of all x x such that the statement about x x is true.” For example,
Interval notation is a way of describing sets that include all real numbers between a lower limit that may or may not be included and an upper limit that may or may not be included. The endpoint values are listed between brackets or parentheses. A square bracket indicates inclusion in the set, and a parenthesis indicates exclusion from the set. For example,
Given a line graph, describe the set of values using interval notation.
- Identify the intervals to be included in the set by determining where the heavy line overlays the real line.
- At the left end of each interval, use [ with each end value to be included in the set (solid dot) or ( for each excluded end value (open dot).
- At the right end of each interval, use ] with each end value to be included in the set (filled dot) or ) for each excluded end value (open dot).
- Use the union symbol ∪ ∪ to combine all intervals into one set.
Describing Sets on the Real-Number Line
Describe the intervals of values shown in Figure 6 using inequality notation, set-builder notation, and interval notation.
To describe the values, x , x , included in the intervals shown, we would say, “ x x is a real number greater than or equal to 1 and less than or equal to 3, or a real number greater than 5.”
Remember that, when writing or reading interval notation, using a square bracket means the boundary is included in the set. Using a parenthesis means the boundary is not included in the set.
Given Figure 7 , specify the graphed set in
- ⓑ set-builder notation
- ⓒ interval notation
Finding Domain and Range from Graphs
Another way to identify the domain and range of functions is by using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x -axis. The range is the set of possible output values, which are shown on the y -axis. Keep in mind that if the graph continues beyond the portion of the graph we can see, the domain and range may be greater than the visible values. See Figure 8 .
We can observe that the graph extends horizontally from −5 −5 to the right without bound, so the domain is [ −5 , ∞ ) . [ −5 , ∞ ) . The vertical extent of the graph is all range values 5 5 and below, so the range is ( −∞ , 5 ] . ( −∞ , 5 ] . Note that the domain and range are always written from smaller to larger values, or from left to right for domain, and from the bottom of the graph to the top of the graph for range.
Finding Domain and Range from a Graph
Find the domain and range of the function f f whose graph is shown in Figure 9 .
We can observe that the horizontal extent of the graph is –3 to 1, so the domain of f f is ( − 3 , 1 ] . ( − 3 , 1 ] .
The vertical extent of the graph is 0 to –4, so the range is [ − 4 , 0 ] . [ − 4 , 0 ] . See Figure 10 .
Finding Domain and Range from a Graph of Oil Production
Find the domain and range of the function f f whose graph is shown in Figure 11 .
The input quantity along the horizontal axis is “years,” which we represent with the variable t t for time. The output quantity is “thousands of barrels of oil per day,” which we represent with the variable b b for barrels. The graph may continue to the left and right beyond what is viewed, but based on the portion of the graph that is visible, we can determine the domain as 1973 ≤ t ≤ 2008 1973 ≤ t ≤ 2008 and the range as approximately 180 ≤ b ≤ 2010. 180 ≤ b ≤ 2010.
In interval notation, the domain is [1973, 2008], and the range is about [180, 2010]. For the domain and the range, we approximate the smallest and largest values since they do not fall exactly on the grid lines.
Given Figure 12 , identify the domain and range using interval notation.
Can a function’s domain and range be the same?
Yes. For example, the domain and range of the cube root function are both the set of all real numbers.
Finding Domains and Ranges of the Toolkit Functions
We will now return to our set of toolkit functions to determine the domain and range of each.
Given the formula for a function, determine the domain and range.
- Exclude from the domain any input values that result in division by zero.
- Exclude from the domain any input values that have nonreal (or undefined) number outputs.
- Use the valid input values to determine the range of the output values.
- Look at the function graph and table values to confirm the actual function behavior.
Finding the Domain and Range Using Toolkit Functions
Find the domain and range of f ( x ) = 2 x 3 − x . f ( x ) = 2 x 3 − x .
There are no restrictions on the domain, as any real number may be cubed and then subtracted from the result.
The domain is ( − ∞ , ∞ ) ( − ∞ , ∞ ) and the range is also ( − ∞ , ∞ ) . ( − ∞ , ∞ ) .
Finding the Domain and Range
Find the domain and range of f ( x ) = 2 x + 1 . f ( x ) = 2 x + 1 .
We cannot evaluate the function at −1 −1 because division by zero is undefined. The domain is ( − ∞ , −1 ) ∪ ( −1 , ∞ ) . ( − ∞ , −1 ) ∪ ( −1 , ∞ ) . Because the function is never zero, we exclude 0 from the range. The range is ( − ∞ , 0 ) ∪ ( 0 , ∞ ) . ( − ∞ , 0 ) ∪ ( 0 , ∞ ) .
Find the domain and range of f ( x ) = 2 x + 4 . f ( x ) = 2 x + 4 .
We cannot take the square root of a negative number, so the value inside the radical must be nonnegative.
The domain of f ( x ) f ( x ) is [ − 4 , ∞ ) . [ − 4 , ∞ ) .
We then find the range. We know that f ( − 4 ) = 0 , f ( − 4 ) = 0 , and the function value increases as x x increases without any upper limit. We conclude that the range of f f is [ 0 , ∞ ) . [ 0 , ∞ ) .
Figure 22 represents the function f . f .
Find the domain and range of f ( x ) = − 2 − x . f ( x ) = − 2 − x .
Graphing Piecewise-Defined Functions
Sometimes, we come across a function that requires more than one formula in order to obtain the given output. For example, in the toolkit functions, we introduced the absolute value function f ( x ) = | x | . f ( x ) = | x | . With a domain of all real numbers and a range of values greater than or equal to 0, absolute value can be defined as the magnitude , or modulus , of a real number value regardless of sign. It is the distance from 0 on the number line. All of these definitions require the output to be greater than or equal to 0.
If we input 0, or a positive value, the output is the same as the input.
If we input a negative value, the output is the opposite of the input.
Because this requires two different processes or pieces, the absolute value function is an example of a piecewise function. A piecewise function is a function in which more than one formula is used to define the output over different pieces of the domain.
We use piecewise functions to describe situations in which a rule or relationship changes as the input value crosses certain “boundaries.” For example, we often encounter situations in business for which the cost per piece of a certain item is discounted once the number ordered exceeds a certain value. Tax brackets are another real-world example of piecewise functions. For example, consider a simple tax system in which incomes up to $10,000 are taxed at 10%, and any additional income is taxed at 20%. The tax on a total income S S would be 0.1 S 0.1 S if S ≤ $ 10 , 000 S ≤ $ 10 , 000 and $ 1000 + 0.2 ( S − $ 10 , 000 ) $ 1000 + 0.2 ( S − $ 10 , 000 ) if S > $ 10 , 000. S > $ 10 , 000.
Piecewise Function
A piecewise function is a function in which more than one formula is used to define the output. Each formula has its own domain, and the domain of the function is the union of all these smaller domains. We notate this idea like this:
In piecewise notation, the absolute value function is
Given a piecewise function, write the formula and identify the domain for each interval.
- Identify the intervals for which different rules apply.
- Determine formulas that describe how to calculate an output from an input in each interval.
- Use braces and if-statements to write the function.
Writing a Piecewise Function
A museum charges $5 per person for a guided tour with a group of 1 to 9 people or a fixed $50 fee for a group of 10 or more people. Write a function relating the number of people, n , n , to the cost, C . C .
Two different formulas will be needed. For n -values under 10, C = 5 n . C = 5 n . For values of n n that are 10 or greater, C = 50. C = 50.
The function is represented in Figure 23 . The graph is a diagonal line from n = 0 n = 0 to n = 10 n = 10 and a constant after that. In this example, the two formulas agree at the meeting point where n = 10 , n = 10 , but not all piecewise functions have this property.
Working with a Piecewise Function
A cell phone company uses the function below to determine the cost, C , C , in dollars for g g gigabytes of data transfer.
Find the cost of using 1.5 gigabytes of data and the cost of using 4 gigabytes of data.
To find the cost of using 1.5 gigabytes of data, C ( 1.5 ) , C ( 1.5 ) , we first look to see which part of the domain our input falls in. Because 1.5 is less than 2, we use the first formula.
To find the cost of using 4 gigabytes of data, C ( 4 ) , C ( 4 ) , we see that our input of 4 is greater than 2, so we use the second formula.
The function is represented in Figure 24 . We can see where the function changes from a constant to a shifted and stretched identity at g = 2. g = 2. We plot the graphs for the different formulas on a common set of axes, making sure each formula is applied on its proper domain.
Given a piecewise function, sketch a graph.
- Indicate on the x -axis the boundaries defined by the intervals on each piece of the domain.
- For each piece of the domain, graph on that interval using the corresponding equation pertaining to that piece. Do not graph two functions over one interval because it would violate the criteria of a function.
Graphing a Piecewise Function
Sketch a graph of the function.
Each of the component functions is from our library of toolkit functions, so we know their shapes. We can imagine graphing each function and then limiting the graph to the indicated domain. At the endpoints of the domain, we draw open circles to indicate where the endpoint is not included because of a less-than or greater-than inequality; we draw a closed circle where the endpoint is included because of a less-than-or-equal-to or greater-than-or-equal-to inequality.
Figure 25 shows the three components of the piecewise function graphed on separate coordinate systems.
Now that we have sketched each piece individually, we combine them in the same coordinate plane. See Figure 26 .
Note that the graph does pass the vertical line test even at x = 1 x = 1 and x = 2 x = 2 because the points ( 1 , 3 ) ( 1 , 3 ) and ( 2 , 2 ) ( 2 , 2 ) are not part of the graph of the function, though ( 1 , 1 ) ( 1 , 1 ) and ( 2 , 3 ) ( 2 , 3 ) are.
Graph the following piecewise function.
Can more than one formula from a piecewise function be applied to a value in the domain?
No. Each value corresponds to one equation in a piecewise formula.
Access these online resources for additional instruction and practice with domain and range.
- Domain and Range of Square Root Functions
- Determining Domain and Range
- Find Domain and Range Given the Graph
- Find Domain and Range Given a Table
- Find Domain and Range Given Points on a Coordinate Plane
3.2 Section Exercises
Why does the domain differ for different functions?
How do we determine the domain of a function defined by an equation?
Explain why the domain of f ( x ) = x 3 f ( x ) = x 3 is different from the domain of f ( x ) = x . f ( x ) = x .
When describing sets of numbers using interval notation, when do you use a parenthesis and when do you use a bracket?
How do you graph a piecewise function?
For the following exercises, find the domain of each function using interval notation.
f ( x ) = − 2 x ( x − 1 ) ( x − 2 ) f ( x ) = − 2 x ( x − 1 ) ( x − 2 )
f ( x ) = 5 − 2 x 2 f ( x ) = 5 − 2 x 2
f ( x ) = 3 x − 2 f ( x ) = 3 x − 2
f ( x ) = 3 − 6 − 2 x f ( x ) = 3 − 6 − 2 x
f ( x ) = 4 − 3 x f ( x ) = 4 − 3 x
f ( x ) = x 2 + 4 f ( x ) = x 2 + 4
f ( x ) = 1 − 2 x 3 f ( x ) = 1 − 2 x 3
f ( x ) = x − 1 3 f ( x ) = x − 1 3
f ( x ) = 9 x − 6 f ( x ) = 9 x − 6
f ( x ) = 3 x + 1 4 x + 2 f ( x ) = 3 x + 1 4 x + 2
f ( x ) = x + 4 x − 4 f ( x ) = x + 4 x − 4
f ( x ) = x − 3 x 2 + 9 x − 22 f ( x ) = x − 3 x 2 + 9 x − 22
f ( x ) = 1 x 2 − x − 6 f ( x ) = 1 x 2 − x − 6
f ( x ) = 2 x 3 − 250 x 2 − 2 x − 15 f ( x ) = 2 x 3 − 250 x 2 − 2 x − 15
f ( x ) = 5 x − 3 f ( x ) = 5 x − 3
f ( x ) = 2 x + 1 5 − x f ( x ) = 2 x + 1 5 − x
f ( x ) = x − 4 x − 6 f ( x ) = x − 4 x − 6
f ( x ) = x − 6 x − 4 f ( x ) = x − 6 x − 4
f ( x ) = x x f ( x ) = x x
f ( x ) = x 2 − 9 x x 2 − 81 f ( x ) = x 2 − 9 x x 2 − 81
Find the domain of the function f ( x ) = 2 x 3 − 50 x f ( x ) = 2 x 3 − 50 x by:
- ⓐ using algebra.
- ⓑ graphing the function in the radicand and determining intervals on the x -axis for which the radicand is nonnegative.
For the following exercises, write the domain and range of each function using interval notation.
For the following exercises, sketch a graph of the piecewise function. Write the domain in interval notation.
f ( x ) = { x + 1 if x < − 2 − 2 x − 3 if x ≥ − 2 f ( x ) = { x + 1 if x < − 2 − 2 x − 3 if x ≥ − 2
f ( x ) = { 2 x − 1 if x < 1 1 + x if x ≥ 1 f ( x ) = { 2 x − 1 if x < 1 1 + x if x ≥ 1
f ( x ) = { x + 1 if x < 0 x − 1 if x > 0 f ( x ) = { x + 1 if x < 0 x − 1 if x > 0
f ( x ) = { 3 if x < 0 x if x ≥ 0 f ( x ) = { 3 if x < 0 x if x ≥ 0
f ( x ) = { x 2 if x < 0 1 − x if x > 0 f ( x ) = { x 2 if x < 0 1 − x if x > 0
f ( x ) = { x 2 x + 2 if x < 0 if x ≥ 0 f ( x ) = { x 2 x + 2 if x < 0 if x ≥ 0
f ( x ) = { x + 1 if x < 1 x 3 if x ≥ 1 f ( x ) = { x + 1 if x < 1 x 3 if x ≥ 1
f ( x ) = { | x | 1 if x < 2 if x ≥ 2 f ( x ) = { | x | 1 if x < 2 if x ≥ 2
For the following exercises, given each function f , f , evaluate f ( −3 ) , f ( −2 ) , f ( −1 ) , f ( −3 ) , f ( −2 ) , f ( −1 ) , and f ( 0 ) . f ( 0 ) .
f ( x ) = { 1 if x ≤ − 3 0 if x > − 3 f ( x ) = { 1 if x ≤ − 3 0 if x > − 3
f ( x ) = { − 2 x 2 + 3 if x ≤ − 1 5 x − 7 if x > − 1 f ( x ) = { − 2 x 2 + 3 if x ≤ − 1 5 x − 7 if x > − 1
For the following exercises, given each function f , f , evaluate f ( −1 ) , f ( 0 ) , f ( 2 ) , f ( −1 ) , f ( 0 ) , f ( 2 ) , and f ( 4 ) . f ( 4 ) .
f ( x ) = { 7 x + 3 if x < 0 7 x + 6 if x ≥ 0 f ( x ) = { 7 x + 3 if x < 0 7 x + 6 if x ≥ 0
f ( x ) = { x 2 − 2 if x < 2 4 + | x − 5 | if x ≥ 2 f ( x ) = { x 2 − 2 if x < 2 4 + | x − 5 | if x ≥ 2
f ( x ) = { 5 x if x < 0 3 if 0 ≤ x ≤ 3 x 2 if x > 3 f ( x ) = { 5 x if x < 0 3 if 0 ≤ x ≤ 3 x 2 if x > 3
For the following exercises, write the domain for the piecewise function in interval notation.
f ( x ) = { x 2 − 2 if x < 1 − x 2 + 2 if x > 1 f ( x ) = { x 2 − 2 if x < 1 − x 2 + 2 if x > 1
f ( x ) = { 2 x − 3 − 3 x 2 if x < 0 if x ≥ 2 f ( x ) = { 2 x − 3 − 3 x 2 if x < 0 if x ≥ 2
Graph y = 1 x 2 y = 1 x 2 on the viewing window [ −0.5 , −0.1 ] [ −0.5 , −0.1 ] and [ 0.1 , 0.5 ] . [ 0.1 , 0.5 ] . Determine the corresponding range for the viewing window. Show the graphs.
Graph y = 1 x y = 1 x on the viewing window [ −0.5 , −0.1 ] [ −0.5 , −0.1 ] and [ 0.1 , 0.5 ] . [ 0.1 , 0.5 ] . Determine the corresponding range for the viewing window. Show the graphs.
Suppose the range of a function f f is [ −5 , 8 ] . [ −5 , 8 ] . What is the range of | f ( x ) | ? | f ( x ) | ?
Create a function in which the range is all nonnegative real numbers.
Create a function in which the domain is x > 2. x > 2.
Real-World Applications
The height h h of a projectile is a function of the time t t it is in the air. The height in feet for t t seconds is given by the function h ( t ) = −16 t 2 + 96 t . h ( t ) = −16 t 2 + 96 t . What is the domain of the function? What does the domain mean in the context of the problem?
The cost in dollars of making x x items is given by the function C ( x ) = 10 x + 500. C ( x ) = 10 x + 500.
- ⓐ The fixed cost is determined when zero items are produced. Find the fixed cost for this item.
- ⓑ What is the cost of making 25 items?
- ⓒ Suppose the maximum cost allowed is $1500. What are the domain and range of the cost function, C ( x ) ? C ( x ) ?
- 3 The Numbers: Where Data and the Movie Business Meet. “Box Office History for Horror Movies.” http://www.the-numbers.com/market/genre/Horror. Accessed 3/24/2014
- 4 http://www.eia.gov/dnav/pet/hist/LeafHandler.ashx?n=PET&s=MCRFPAK2&f=A.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
- Authors: Jay Abramson
- Publisher/website: OpenStax
- Book title: College Algebra 2e
- Publication date: Dec 21, 2021
- Location: Houston, Texas
- Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
- Section URL: https://openstax.org/books/college-algebra-2e/pages/3-2-domain-and-range
© Jun 28, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Want Better Math Grades?
✅ Unlimited Solutions
✅ Step-by-Step Answers
✅ Available 24/7
➕ Free Bonuses ($1085 value!)
On this page
- Introduction to Geometry
- Functions and Graphs
- 1. Introduction to Functions
- 2. Functions from Verbal Statements
- 3. Rectangular Coordinates
- 4. The Graph of a Function
- 4a. Domain and Range of a Function
- 4b. Domain and Range interactive applet
- 4c. Comparison calculator BMI - BAI
- 5. Graphing Using a Computer Algebra System
- 5a. Online graphing calculator (1): Plot your own graph (JSXGraph)
- 5b. Online graphing calculator (2): Plot your own graph (SVG)
- 6. Graphs of Functions Defined by Tables of Data
- 7. Continuous and Discontinuous Functions
- 8. Split Functions
- 9. Even and Odd Functions
Related Sections
Math Tutoring
Need help? Chat with a tutor anytime, 24/7.
Online Math Solver
Solve your math problem step by step!
IntMath Forum
Get help with your math queries:
Domain and Range of a Function
Definitions of domain and range, domain and range worksheet.
Download this Domain and Range worksheet with 10 questions and answers as a practice test.
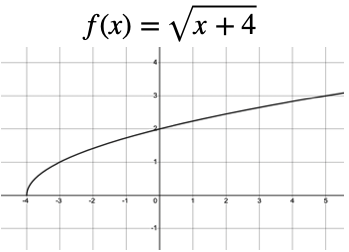
Domain and Range Worksheet with Answers
The domain of a function is the complete set of possible values of the independent variable.
In plain English, this definition means:
The domain is the set of all possible x -values which will make the function "work", and will output real y -values.
When finding the domain , remember:
- The denominator (bottom) of a fraction cannot be zero
- The number under a square root sign must be positive in this section
Domain & Range Math Problem Solver
This tool combines the power of mathematical computation engine that excels at solving mathematical formulas with the power of GPT large language models to parse and generate natural language. This creates math problem solver thats more accurate than ChatGPT, more flexible than a calculator, and faster answers than a human tutor.
Domain and Range Interactive
After finishing this lesson head over to our interactive calculator to help you find the Domain and Range of a Fuction.
Here is the graph of `y = sqrt(x+4)`:
Graphing Calculator
Need a graphing calculator? Read our review here:
TI-NSpire: The Most Powerful Calculator
The domain of this function is `x ≥ −4`, since x cannot be less than ` −4`. To see why, try out some numbers less than `−4` (like ` −5` or ` −10`) and some more than `−4` (like ` −2` or `8`) in your calculator. The only ones that "work" and give us an answer are the ones greater than or equal to ` −4`. This will make the number under the square root positive.
- The enclosed (colored-in) circle on the point `(-4, 0)`. This indicates that the domain "starts" at this point.
- We saw how to draw similar graphs in section 4, Graph of a Function . For a more advanced discussion, see also How to draw y^2 = x − 2 .
How to find the domain
In general, we determine the domain of each function by looking for those values of the independent variable (usually x ) which we are allowed to use. (Usually we have to avoid 0 on the bottom of a fraction, or negative values under the square root sign).
The range of a function is the complete set of all possible resulting values of the dependent variable ( y, usually), after we have substituted the domain.
In plain English, the definition means:
The range is the resulting y- values we get after substituting all the possible x -values.
How to find the range
- The range of a function is the spread of possible y -values (minimum y -value to maximum y -value)
- Substitute different x -values into the expression for y to see what is happening. (Ask yourself: Is y always positive? Always negative? Or maybe not equal to certain values?)
- Make sure you look for minimum and maximum values of y .
- Draw a sketch! In math, it's very true that a picture is worth a thousand words.
Let's return to the example above, `y = sqrt(x + 4)`.
We notice the curve is either on or above the horizontal axis. No matter what value of x we try, we will always get a zero or positive value of y . We say the range in this case is y ≥ 0.
The curve goes on forever vertically, beyond what is shown on the graph, so the range is all non-negative values of `y`.
The graph of the curve y = sin x shows the range to be betweeen −1 and 1.
The domain of y = sin x is "all values of x ", since there are no restrictions on the values for x . (Put any number into the "sin" function in your calculator. Any number should work, and will give you a final answer between −1 and 1.)
From the calculator experiment, and from observing the curve, we can see the range is y betweeen −1 and 1 . We could write this as −1 ≤ y ≤ 1.
Where did this graph come from? We learn about sin and cos graphs later in Graphs of sin x and cos x
Note 1: Because we are assuming that only real numbers are to be used for the x -values, numbers that lead to division by zero or to imaginary numbers (which arise from finding the square root of a negative number) are not included. The Complex Numbers chapter explains more about imaginary numbers, but we do not include such numbers in this chapter.
Note 2: When doing square root examples, many people ask, "Don't we get 2 answers, one positive and one negative when we find a square root?" A square root has at most one value, not two. See this discussion: Square Root 16 - how many answers?
Note 3: We are talking about the domain and range of functions , which have at most one y -value for each x -value, not relations (which can have more than one.).
Finding domain and range without using a graph
It's always a lot easier to work out the domain and range when reading it off the graph (but we must make sure we zoom in and out of the graph to make sure we see everything we need to see). However, we don't always have access to graphing software, and sketching a graph usually requires knowing about discontinuities and so on first anyway.
As meantioned earlier, the key things to check for are:
- There are no negative values under a square root sign
- There are no zero values in the denominator (bottom) of a fraction
Find the domain and range of the function `f(x)=sqrt(x+2)/(x^2-9),` without using a graph.
In the numerator (top) of this fraction, we have a square root. To make sure the values under the square root are non-negative, we can only choose `x`-values grater than or equal to -2.
The denominator (bottom) has `x^2-9`, which we recognise we can write as `(x+3)(x-3)`. So our values for `x` cannot include `-3` (from the first bracket) or `3` (from the second).
We don't need to worry about the `-3` anyway, because we dcided in the first step that `x >= -2`.
So the domain for this case is `x >= -2, x != 3`, which we can write as `[-2,3)uu(3,oo)`.
To work out the range, we consider top and bottom of the fraction separately.
Numerator: If `x=-2`, the top has value `sqrt(2+2)=sqrt(0)=0`. As `x` increases value from `-2`, the top will also increase (out to infinity in both cases).
Denominator: We break this up into four portions:
When `x=-2`, the bottom is `(-2)^2-9=4-9=-5`. We have `f(-2) = 0/(-5) = 0.`
Between `x=-2` and `x=3`, `(x^2-9)` gets closer to `0`, so `f(x)` will go to `-oo` as it gets near `x=3`.
For `x>3`, when `x` is just bigger than `3`, the value of the bottom is just over `0`, so `f(x)` will be a very large positive number.
For very large `x`, the top is large, but the bottom will be much larger, so overall, the function value will be very small.
So we can conclude the range is `(-oo,0]uu(oo,0)`.
Have a look at the graph (which we draw anyway to check we are on the right track):
We can see in the following graph that indeed, the domain is `[-2,3)uu(3,oo)` (which includes `-2`, but not `3`), and the range is "all values of `f(x)` except `F(x)=0`."
Graph of `f(x)=sqrt(x+2)/(x^2-9)`.
In general, we determine the domain by looking for those values of the independent variable (usually x ) which we are allowed to use. (We have to avoid 0 on the bottom of a fraction, or negative values under the square root sign).
The range is found by finding the resulting y -values after we have substituted in the possible x -values.
Find the domain and range for each of the following.
(a) `f(x) = x^2+ 2`.
Domain: The function
f ( x ) = x 2 + 2
is defined for all real values of x (because there are no restrictions on the value of x ).
Hence, the domain of `f(x)` is
"all real values of x ".
Range: Since x 2 is never negative, x 2 + 2 is never less than `2`
Hence, the range of `f(x)` is
"all real numbers `f(x) ≥ 2`".
We can see that x can take any value in the graph, but the resulting y = f ( x ) values are greater than or equal to 2.
- It is important to label the axes when sketching graphs. It helps with understanding what the graph represents.
- We saw how to sketch such graphs in Graph of a Function .
Need Graph Paper?
(b) `f(t)=1/(t+2)`
`f(t)=1/(t+2)`
is not defined for t = -2, as this value would result in division by zero. (There would be a 0 on the bottom of the fraction.)
Hence the domain of f ( t ) is
"all real numbers except -2"
Range: No matter how large or small t becomes, f ( t ) will never be equal to zero.
[ Why? If we try to solve the equation for 0, this is what happens:
`0=1/(t+2)`
Multiply both sides by ( t + 2) and we get
This is impossible.]
So the range of f ( t ) is
"all real numbers except zero".
We can see in the graph that the function is not defined for `t = -2` and that the function (the y -values) takes all values except `0`.
(c) `g(s)=sqrt(3-s)`
The function
`g(s)=sqrt(3-s)`
is not defined for real numbers greater than 3, which would result in imaginary values for g ( s ).
Hence, the domain for g ( s ) is "all real numbers, s ≤ 3".
Also, by definition,
`g(s)=sqrt(3-s) >= 0`
Hence, the range of g ( s ) is "all real numbers `g(s) ≥ 0`"
We can see in the graph that s takes no values greater than 3, and that the range is greater than or equal to `0`.
(d) `f(x) = x^2+ 4` for `x > 2`
The function `f(x)` has a domain of "all real numbers, `x > 2`" as defined in the question. (There are no resulting square roots of negative numbers or divisions by zero involved here.)
To find the range :
- When `x = 2`, `f(2) = 8`
- When x increases from `2`, `f(x)` becomes larger than `8` (Try substituting in some numbers to see why.)
Hence, the range is "all real numbers, `f(x) > 8`"
Here is the graph of the function, with an open circle at `(2, 8)` indicating that the domain does not include `x = 2` and the range does not include `f(2) = 8`.
The function is part of a parabola. [See more on parabola .]
More Domain and Range Examples
In case you missed it earlier, you can see more examples of domain and range in the section Inverse Trigonometric Functions .
See also Domain and Range Calculator .
We fire a ball up in the air and find the height h , in metres, as a function of time t , in seconds, is given by
h = 20 t − 4.9 t 2
Find the domain and range for the function h ( t ).
Generally, negative values of time do not have any meaning. Also, we need to assume the projectile hits the ground and then stops - it does not go underground.
So we need to calculate when it is going to hit the ground. This will be when h = 0. So we solve:
20 t − 4.9 t 2 = 0
Factoring gives:
(20 − 4.9 t ) t = 0
This is true when
`t = 0\ "s"`,
`t=20/4.9 = 4.082 text(s)`
Hence, the domain of the function h is
"all real values of t such that `0 ≤ t ≤ 4.082`"
We can see from the function expression that it is a parabola with its vertex facing up. (This makes sense if you think about throwing a ball upwards. It goes up to a certain height and then falls back down.)
What is the maximum value of h ? We use the formula for maximum (or minimum) of a quadratic function .
The value of t that gives the maximum is
`t = -b/(2a) = -20/(2 xx (-4.9)) = 2.041 s `
So the maximum value is
20(2.041) − 4.9(2.041) 2 = 20.408 m
By observing the function of h , we see that as t increases, h first increases to a maximum of 20.408 m, then h decreases again to zero, as expected.
Hence, the range of h is
"all real numbers, `0 ≤ h ≤ 20.408`"
Here is the graph of the function h :
Functions defined by coordinates
Sometimes we don't have continuous functions. What do we do in this case? Let's look at an example.
Find the domain and range of the function defined by the coordinates:
`{(−4, 1), (−2, 2.5), (2, −1), (3, 2)}`
The domain is simply the x -values given: `x = {−4, −2, 2, 3}`
The range consists of the `f(x)`-values given: `f(x) = {−1, 1, 2, 2.5}`
Here is the graph of our discontinuous function.
Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.
Email Address Sign Up
- Math Article
- Domain Codomain Range Functions
Domain Range and Codomain Of A Function

We are familiar with the terms Domain of a Function and Range of a Function. But what does it mean? Before diving deeper into the topic, let us understand what a function is? Then, get into the detailed explanation of the domain, range and codomain of a function , along with solved examples.
Functions are one of the fundamental concepts in mathematics which have got numerous applications in the real world. Be it the mega skyscrapers or super-fast cars, their modelling requires methodical application of functions. Almost all real-world problems are formulated, interpreted, and solved using functions.
An understanding of relations is required to learn functions, Knowledge of Cartesian products is also required to learn about relations in maths. A Cartesian product of two sets A and B is the collection of all the ordered pairs (a, b) such that a ∈ A and b ∈ B.
Learn: Cartesian product
A relation is a subset of a Cartesian product. Thus, a relation is a rule that “relates” an element from one set to another. A function is a special kind of relation. Let’s consider a relation F from A set A to B
Definition: A relation F is said to be a function if each element in set A is associated with exactly one element in set B.
To understand the difference between relations and functions with the help of an example.
Set A = Names of all countries that won the cricket world cup
Set B = List of years in which the world cup played
The arrow diagram shows (in the figure below) the relation R but not a function.
This is because elements of set A are associated with more than one element of set B.
Suppose we define a relation F from set A to B such that it associates the countries with the year in which they won the world cup for the first time. Thus, every element in set A will be exactly associated with only one element in set B.
This relation F shown in the below figure is qualified to be a function.
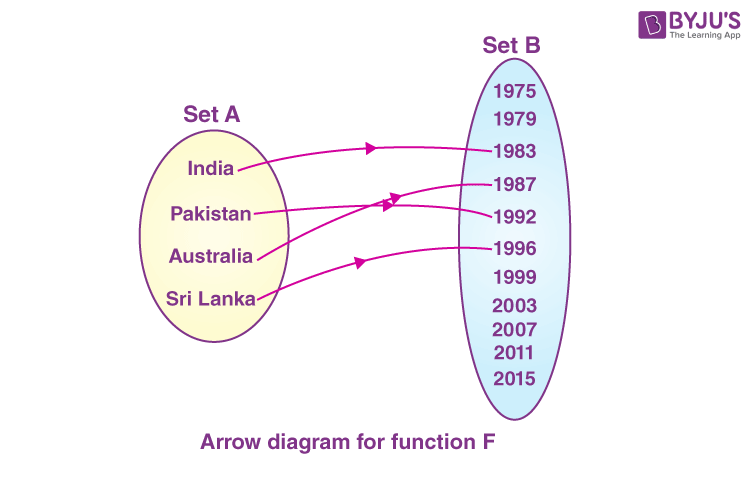
Domain and Range
The domain and range of a function can be identified based on the possibility of the given function to be defined in the real set. Let’s have a look at Domain and Range that is given in detail here.
The set of all possible values which qualify as inputs to a function is known as the domain of the function, or it can also be defined as the entire set of values possible for independent variables. The domain can be found in – the denominator of the fraction is not equal to zero and the digit under the square root bracket is positive. (In the case of a function with fraction values).
For e.g. the domain of the function F is set A i.e. {India, Pakistan, Australia, Sri Lanka}.
How to Find the Domain of a function
- To find the domain, we need to look at the values of the independent variables which are allowed to use as explained above, i.e. no zero at the bottom of the fraction and no negative sign inside the square root.
- In general, the set of all real numbers (R) is considered as the domain of a function subject to some restrictions. They are: When the given function is of the form f(x) = 2x + 5 or f(x) = x 2 – 2, the domain will be “the set of all real numbers. When the given function is of the form f(x) = 1/(x – 1), the domain will be the set of all real numbers except 1.
- In some cases, the interval be specified along with the function such as f(x) = 3x + 4, 2 < x < 12. Here, x can take the values between 2 and 12 as input (i.e. domain).
- Domain restrictions refer to the values for which the given function cannot be defined.
Also, try: Domain and Range Calculator
The set of all the outputs of a function is known as the range of the function or after substituting the domain, the entire set of all values possible as outcomes of the dependent variable.
For e.g. the range of the function F is {1983, 1987, 1992, 1996}. On the other hand, the whole set B is known as the codomain of the function. It is the set that contains all the outputs of the function. So, the set of real numbers is a codomain for every real-valued function. The codomain of the function F is set B .
Video Lesson
Range of a function.

How to Find the Range of a Function
Consider a function y = f(x).
- The spread of all the y values from minimum to maximum is the range of the function.
- In the given expression of y, substitute all the values of x to check whether it is positive, negative or equal to other values.
- Find the minimum and maximum values for y.
- Then draw a graph for the same.
In relations and functions, the codomain is the set of all possible outcomes of the given relation or function. Sometimes, the codomain is also equal to the range of the function. However, the range is the subset of the codomain.
An interesting point about the range and codomain is that “it is possible to restrict the range (i.e. the output of a function) by redefining the codomain of that function”. For example, the codomain of f(x) must be the set of all positive integers or negative real numbers and so on. Here, the output of the function must be a positive integer and the domain will also be restricted accordingly in this case.
Till now, we have represented functions with upper case letters but they are generally represented by lower case letters. If f is a function from set A to B and (a,b) ∈ f , then f(a) = b . b is called the image of a under f and a is called the preimage of b under f .
- The domain is defined as the entire set of values possible for independent variables.
- The Range is found after substituting the possible x- values to find the y-values.

Solved Examples
Find the domain and range of a function f(x) = 3x 2 – 5.
Given function:
f(x) = 3x 2 – 5
We know that the domain of a function is the set of input values for f, in which the function is real and defined.
The given function has no undefined values of x.
Thus, for the given function, the domain is the set of all real numbers.
Domain = [- ∞, ∞]
Also, the range of a function comprises the set of values of a dependent variable for which the given function is defined.
Ley y = 3x 2 – 5
3x 2 = y + 5
x 2 = (y + 5)/3
x = √[(y + 5)/3]
Square root function will be defined for non-negative values.
So, √[(y + 5)/3] ≥ 0
This is possible when y is greater than y ≥ -5.
Hence, the range of f(x) is [-5, ∞).
Find the domain and range of a function f(x) = (2x – 1)/(x + 4).
Given function is:
f(x) = (2x – 1)/(x + 4)
The given function is not defined when x + 4 = 0, i.e. x = -4
So, the domain of given function is the set of all real number except -4.
i.e. Domain = (-∞, -4) U (-4, ∞)
Let y = (2x – 1)/(x + 4)
xy + 4y = 2x – 1
2x – xy = 4y + 1
x(2 – y) = 4y + 1
x = (4y + 1)/(2 – y)
This is defined only when y is not equal to 2.
Hence, the range of the given function is (-∞, 2) U (2, ∞).
Practice Problems
- Find the domain and range of the function f(x) = 1/x.
- Write the domain set for this function f(x) = 1/(x 3 − 3x 2 − 6x − 8).
- What is the domain, codomain and range of the function f(x) = 4/ √(x – 1).
Domain, Range and Period of Function

There are several types of functions and some of them have got funny names e.g. floor function, ceiling function, etc. To know more, visit www.byjus.com and experience fun in learning.
Recommended Videos
Relations and types of relations.

Functions – Introduction, Co-domain and Range

Functions and Types of Functions

Range of Functions – Concepts & Questions

Frequently Asked Questions – FAQs
What is the difference between domain and codomain, how do you find the domain of a function, what is the easiest way of writing the range of a function, can range be equal to codomain, is codomain a subset of range.
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
Domain, Range and Codomain
In its simplest form the domain is all the values that go into a function, and the range is all the values that come out.
But in fact they are very important in defining a function. Read on!
Please read What is a Function? first.
A function relates an input to an output:

Example: this tree grows 20 cm every year, so the height of the tree is related to its age using the function h :
h (age) = age × 20
So, if the age is 10 years, the height is h (10) = 200 cm
Saying " h (10) = 200 " is like saying 10 is related to 200. Or 10 → 200
Input and Output
But not all values may work!
- The function may not work if we give it the wrong values (such as a negative age),
- And knowing the values that can come out (such as always positive) can also help
So we need to say all the values that can go into and come out of a function.
This is best done using Sets ...
A set is a collection of things, such as numbers.
Here are some examples:
In fact, a function is defined in terms of sets:
Domain, Codomain and Range
There are special names for what can go into , and what can come out of a function:
| What can go a function is called the | |
| What of a function is called the | |
| What of a function is called the |
• The set "A" is the Domain ,
• The set "B" is the Codomain ,
• And the set of elements that get pointed to in B (the actual values produced by the function) are the Range , also called the Image.
And we have:
- Domain: {1, 2, 3, 4}
- Codomain: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
- Range: {3, 5, 7, 9}
Part of the Function
Now, what comes out (the Range) depends on what we put in (the Domain) ...
... but WE can define the Domain!
In fact the Domain is an essential part of the function. Change the Domain and we have a different function.
Example: a simple function like f(x) = x 2 can have the domain (what goes in) of just the counting numbers {1,2,3,...}, and the range will then be the set {1,4,9,...}
And another function g(x) = x 2 can have the domain of integers {...,-3,-2,-1,0,1,2,3,...}, in which case the range is the set {0,1,4,9,...}
| Even though both functions take the input and square it, they have a , and so give a different set of outputs. In this case the range of g(x) also includes 0. | |
| Also they will have different properties. For example f(x) always gives a unique answer, but g(x) can give the same answer with two different inputs (such as , and also ) |
So, the domain is an essential part of the function.
Does Every Function Have a Domain?
Yes, but in simpler mathematics we never notice this, because the domain is assumed :
- Usually it is assumed to be something like "all numbers that will work".
- Or if we are studying whole numbers, the domain is assumed to be whole numbers.
But in more advanced work we need to be more careful!
Codomain vs Range
The Codomain and Range are both on the output side, but are subtly different.
The Codomain is the set of values that could possibly come out. The Codomain is actually part of the definition of the function.
And The Range is the set of values that actually do come out.
Example: we can define a function f(x)=2x with a domain and codomain of integers (because we say so).
But by thinking about it we can see that the range (actual output values) is just the even integers.
So the codomain is integers (we defined it that way), but the range is even integers.
The Range is a subset of the Codomain.
Why both? Well, sometimes we don't know the exact range (because the function may be complicated or not fully known), but we know the set it lies in (such as integers or reals). So we define the codomain and continue on.
The Importance of Codomain
Let me ask you a question: Is square root a function?
If we say the codomain (the possible outputs) is the set of real numbers , then square root is not a function ! ... is that a surprise?
The reason is that there could be two answers for one input, for example f(9) = 3 or -3
A function must be single valued . It cannot give back 2 or more results for the same input. So "f(9) = 3 or -3" is not right!
But it can be fixed by simply limiting the codomain to non-negative real numbers.
√ In fact, the radical symbol (like √x ) always means the principal (positive) square root, so √x is a function because its codomain is correct.
So, what we choose for the codomain can actually affect whether something is a function or not.
Mathematicians don't like writing lots of words when a few symbols will do. So there are ways of saying "the domain is", "the codomain is", etc.
This is the neatest way I know:
| this says that the function " " has a domain of " " (the ), and a codomain of " " also. | |
| | and either of these say that the function "f" takes in "x" and returns "x " |
There is also:
Dom(f) or Dom f meaning "the domain of the function f"
Ran(f) or Ran f meaning "the range of the function f"
How to Specify Domains and Ranges
Learn how to specify Domains and Ranges at Set Builder Notation .
Become a math whiz with AI Tutoring, Practice Questions & more.
Domain and Range of Exponential and Logarithmic Functions
Recall that the domain of a function is the set of input or x -values for which the function is defined, while the range is the set of all the output or y -values that the function takes.
A simple exponential function like f ( x ) = 2 x has as its domain the whole real line. But its range is only the positive real numbers, y > 0 : f ( x ) never takes a negative value. Furthermore, it never actually reaches 0 , though it approaches asymptotically as x goes to − ∞ .
If we replace x with − x to get the equation g ( x ) = 2 − x , the graph gets reflected around the y -axis, but the domain and range do not change:
If we put a negative sign in frontto get the equation h ( x ) = − 2 x , the graph gets reflected around the x -axis. We still have the whole real line as our domain, but the range is now the negative numbers, y < 0 .
Now, consider the function f ( x ) = ( − 2 ) x . When x = 1 2 , y must be a complex number, so things get tricky. For this lesson we will require that our bases be positive for the moment, so that we can stay in the real-valued world.
In general, the graph of the basic exponential function y = a x drops from ∞ to 0 when 0 < a < 1 as x varies from − ∞ to ∞ and rises from 0 to ∞ when a > 1 .
The exponential function y = a x , can be shifted k units vertically and h units horizontally with the equation y = a ( x + h ) + k . Then the domain of the function remains unchanged and the range becomes { y ∈ ℝ | y > h } .
Find the domain and range of the function y = 3 x + 2 .
Graph the function on a coordinate plane.
The graph is nothing but the graph y = 3 x translated 2 units to the left.
The function is defined for all real numbers. So, the domain of the function is set of real numbers.
As x tends to ∞ , the value of the function also tends to ∞ and as x tends to − ∞ , the function approaches the x -axis but never touches it.
Therefore, the range of the function is set of real positive numbers or { x ∈ ℝ | x > 0 } .
Find the domain and range of the function y = ( 1 4 ) 2 x .
The graph is nothing but the graph y = ( 1 4 ) x compressed by a factor of 2 .
As x tends to ∞ , the value of the function tends to zero and the graph approaches x -axis but never touches it.
As x tends to − ∞ , the function also tends to ∞ .
Therefore, the range of the function is set of real positive numbers or { y ∈ ℝ | y > 0 } .
The inverse of an exponential function is a logarithmic function.
A simple logarithmic function y = log 2 x where x > 0 is equivalent to the function x = 2 y . That is, y = log 2 x is the inverse of the function y = 2 x .
The function y = log 2 x has the domain of set of positive real numbers and the range of set of real numbers.
Remember that since the logarithmic function is the inverse of the exponential function, the domain of logarithmic function is the range of exponential function, and vice versa.
In general, the function y = log b x where b , x > 0 and b ≠ 1 is a continuous and one-to-one function. Note that the logarithmic functionis not defined for negative numbers or for zero. The graph of the function approaches the y -axis as x tends to ∞ , but never touches it.
Therefore, the domain of the logarithmic function y = log b x is the set of positive real numbers and the range is the set of real numbers.
The function rises from − ∞ to ∞ as x increases if b > 1 and falls from ∞ to − ∞ as x increases if 0 < b < 1 .
The logarithmic function, y = log b x , can be shifted k units vertically and h units horizontally with the equation y = log b ( x + h ) + k . Then the domain of the function becomes { x ∈ ℝ | x > − h } . However, the range remains the same.
Find the domain and range of the function y = log ( x ) − 3 .
Graph the function on a coordinate plane.Remember that when no base is shown, the base is understood to be 10 .
The graph is nothing but the graph y = log ( x ) translated 3 units down.
The function is defined for only positive real numbers. So, the domain of the function is set of positive real numbers or { x ∈ ℝ | x > 0 } .
The function takes all the real values from − ∞ to ∞ .
Therefore, the range of the function is set of real numbers.
Find the domain and range of the function y = log 3 ( x − 2 ) + 4 .
The graph is nothing but the graph y = log 3 ( x ) translated 2 units to the right and 4 units up.
As x tends to 2 , the function approaches the line x = 2 but never touches it. As x tends to ∞ the value of the function also tends to ∞ . That is, the function is defined for real numbers greater than 2 . So, the domain of the function is set of positive real numbers or { x ∈ ℝ | x > 2 } .
- PCAT Test Prep
- WEST-E Courses & Classes
- IB Design Technology Tutors
- SHSAT Test Prep
- Kansas Bar Exam Test Prep
- Iranian History Tutors
- FTCE - Florida Teacher Certification Examinations Courses & Classes
- CFP Test Prep
- COMLEX Test Prep
- REGENTS U.S History Tutors
- SSAT- Middle Level Tutors
- PHR - Professional in Human Resources Test Prep
- AAI - Accredited Adviser in Insurance Test Prep
- Actuarial Exam FM Courses & Classes
- Series 86 Courses & Classes
- Modern Cryptography Tutors
- CMA - Certified Management Accountant Courses & Classes
- Planetary Geology Tutors
- CAE - Certified Association Executive Exam Test Prep
- MAP Test Prep
- Houston Tutoring
- Madison Tutoring
- Nashville Tutoring
- Louisville Tutoring
- Tucson Tutoring
- Milwaukee Tutoring
- Kansas City Tutoring
- Ann Arbor Tutoring
- Virginia Beach Tutoring
- Boulder Tutoring
- ACT Tutors in Chicago
- MCAT Tutors in Chicago
- Biology Tutors in Washington DC
- Spanish Tutors in San Francisco-Bay Area
- Spanish Tutors in Philadelphia
- ACT Tutors in Dallas Fort Worth
- Algebra Tutors in Dallas Fort Worth
- GMAT Tutors in Seattle
- Calculus Tutors in Washington DC
- ISEE Tutors in Denver

for World Environment Day with code NATURE30

Share this article

Table of Contents
Latest updates.

Ways To Improve Learning Outcomes: Learn Tips & Tricks

Visual Learning Style for Students: Pros and Cons

NCERT Books for Class 6 Social Science 2024 – Download PDF

CBSE Syllabus for Class 9 Social Science 2023-24: Download PDF

CBSE Syllabus for Class 8 Maths 2024: Download PDF

NCERT Books for Class 6 Maths 2025: Download Latest PDF

CBSE Class 10 Study Timetable 2024 – Best Preparation Strategy

CBSE Class 10 Syllabus 2025 – Download PDF

CBSE Syllabus for Class 11 2025: Download PDF

NCERT Solutions for Class 7 Science Chapter 16 Water – A Precious Resource
Tag cloud :.
- entrance exams
- engineering
- ssc cgl 2024
- Written By Priya Wadhwa
- Last Modified 25-01-2023
Domain and Range of Relation: Definition, Formulas & Examples
Domain and Range of Relation: A relation is a rule that connects elements in one set to those in another. \(A\) and \(B\) If are non-empty sets, then the relationship is a subset of Cartesian Product \(A \times B\).
The domain is the set of initial members of all ordered pairs. On the other hand, the range is the collection of all ordered pairs’ second components and only comprises the items utilised by the function. In this article, we will discuss the domain and range of relations in detail.
Introduction
We necessarily know questions such as, “How is he connected to you?” in our daily lives. The below are some appropriate options:
(i) He is my father. (ii) He is my teacher. (iii) He is not related to me.

Domain and Range of Functions
As a result, we may conclude that the term relation refers to a connection between two people. In mathematics, extending this concept, a relation is defined as a link between two or more mathematical objects. Examples,
(i) A number \(m\) is related to a number \(n\) if \(m\) divides \(n\) in the set of \(N\) (ii) A real number \(x\) is related to a real number \(x \le y.\) (iii) A point \(p\) is related to a line \(L\) if \(p\) lies on \(L\). (iv) A student \(X\) is related to a school \(S\) if \(X\) is a student of \(S\).
What is a Relation?
The ordered pair collection is defined as the relationship between two sets in which the object from each set forms the ordered pair. A relation \(R\) is the subset of the cartesian product of any two non-empty sets \(A\) and \(B\). According to the relation, every element of one set is mapped to one or more elements of the other set.
In terms of relationships, we may say that every input has one or more outputs. If \((a,\,b) \in \,R\) we say that \(a\) is related to \(b\) under the relation \(R\) and is written as a \(R\,b\). The function is a particular connection in which elements from one set are mapped to just one set’s element.

A set of ordered pairs is referred to as a relation in mathematics. An arrow diagram shows the relationship \((R\,:A \to B)\) between sets \(A\) and \(B\) in the image below.

There is a relationship between sets \(A\) and \(B\) in the diagram above. Ordered pairs can be finite or infinite in a relation. The term “relation on \(A”\) refers to a relationship between sets \(A\) and \(A\). \({2^{mn}}\) is the maximum number of relations defined from sets \(A\) (with \(m\) elements) and (with \(n\) elements).
Domain and Range of a Relation
Now it’s clear that, like a Cartesian product, a relationship will have ordered pairs. The second element in these ordered pairings is the image of the first element, while the first element is the preimage of the second element.
This implies that one set will have all the preimages, while the other will contain all the images. The relation domain is the set that contains all the initial elements of all the ordered pairs of relation The domain set may or may not be identical to set \(R\) The domain set may or may not be identical to set \(A\). The range of the relation, on the other hand, is the set that contains all the second items. The second set \(B\) might be the same size as or more significant than the relation’s range.
This is because elements in set \(B\) might be unrelated to any element in set \(A\). As a result, the entire set \(B\) is known by a new name, i.e. the relation’s codomain. Relations can be expressed in the same manner as the sets are represented, i.e., using the Roster technique or the Set-builder approach. The use of arrow diagrams provides another more precise depiction.
For example, consider the set \(N = \left\{ {9,10,\,11,\,12,\,13} \right\}\). Let us now create a relation \(A\) from \(N\) to \(N\) such that \(y\) is two greater than \(x\) in the ordered pair \((x,\,y)\) in \(A\). This can be expressed in one of three ways:
- Set-builder method: \(A = \left\{ {(x,\,y):y = x + 2;\,x,\,y \in N} \right\}\)
- Roster method: \(A = \left\{ {(9,\,11),\,(10,\,12),\,(11,\,13)} \right\}\)
- Arrow diagram:

Since the domain of \(A\) is not \(N\) It is equal to \(\left\{ {9,\,10,\,11} \right\}\) Because for other values from \(N\) the output doesn’t lie in set \(N\) Also, the codomain of \(A\) is \(N\) But the range of \(A\) is \(\left\{ {11,\,12,\,13} \right\}\) , which is a subset of the codomain.

Relation Representation
Apart from set notation, there are various ways to express the relation, such as using tables, plotting it on an \(XY – \) axis, or using a mapping diagram.

Types of Relations
Following are the different types of relations:
1. Empty Relation
The relation \(R\) in \(A\) is an empty relation, also known as the void relation when no element of set \(A\) is connected or mapped to any other member of \(A\).
For instance, suppose the fruit basket contains \(100\) mangoes. There is no way to find a mangoes. There is no way to find a relation \(R\) that will result in an apple being placed in the basket. is Void because it has \(100\) mangoes but no apples.
2. Universal Relation
A set \(A\) is a universal relation if every element of \(A\) is connected to every element of \(A\) in this entire relation. For example, \(R\, = \,A \times A\) is a universal relation
3. Identity Relation
Identity relation occurs when each element of set \(A\) is only related to itself.
\({I_A} = \,\{ (a,\,a),\,a \in R\} \)
For example,
When we roll the dice, there are a total of \(36\) possible outcomes, i.e.,
\(\left\{ {(1,\,\,1),\,(1,\,\,2),\,(1,\,\,3)……(6,\,6)} \right\}\) From these, if we consider the relation \(\left\{ {(1,\,\,1),\,(2,\,\,2),\,(3,\,\,3),\,(4,\,\,4),\,(5,\,\,5),(6,\,\,6)} \right\}\) , it is an identity relation.
4. Inverse Relation
If \(R\) is a relation from \(A\) set to set \(B\) such that \(R \in \,\,A \times B\) then relation \({R^{ – 1}} = \,\{ (b,\,\,a);(a,\,b) \in R\} \) For example,
If we roll two dice and if \(R = \,\{ (1,\,\,2),(2,\,3)\} \) then \({R^{ – 1}} = \,\{ (2,\,\,1),(3,\,2)\} \) Here the domain of is the range of \(R\) is the range of \({R^{ – 1}}\) and vice versa.
5 . Reflexive Relation
If every element of set \(A\) maps to itself, then the relation is reflexive. i.e for every \(a \in \,A,\,(a,\,a) \in R\)
6. Symmetric Relation
A relation \(R\) on a set \(A\) is symmetric if \((a,\,\,b) \in R\) then \((b,\,\,a) \in R\) for all \(a,\,\,b \in A\)
7. Transitive Relation
A relation \(R\) on a set \(A\) is said to be transitive if \((a,\,\,b) \in R,\,(b,\,c) \in R\) then \((a,\,\,c) \in R,\) for all \(a,\,b,\,c \in A\)
8. Equivalence Relation
A relation \(R\) on a set \(A\) is an equivalence relation if it is reflexive, symmetric and transitive.

Solved Examples – Domain and Range of Relations
Q.1. Write the domain and range of the given relation: (eye colour, student’s name). \(a,b,\,c \in A = \{ \left( {{\rm{blue}},\,{\rm{John}}} \right),\,\left( {{\rm{green}},\,{\rm{William}}} \right),\,\left( {{\rm{brown}},\,{\rm{Wilson}}} \right),\,\left( {{\rm{blue}},\,{\rm{Moy}}} \right)\) \(\left( {{\rm{brown}},\,{\rm{Abraham}}} \right),\,\left( {{\rm{green}},\,{\rm{Dutt}}} \right)\} \) State whether the relation is a function. Ans: Domain: \(\left\{ {{\rm{blue}},\,{\rm{green}},\,{\rm{brown}}} \right\}\) Range: \(\left\{ {{\rm{John}},\,{\rm{William}},\,{\rm{Wilson}},\,{\rm{Moy}},\,{\rm{Abraham}},\,{\rm{Dutt}}} \right\}\) Because the eye colours are repeated, the relationship is not a function.
Q.2. Write the domain and range of the given relation: \(\{ (4,\,3),\,( – 1,\,7),\,(2,\, – 3),\,(7,\,\,5),\,(6,\, – 2)\} \) Ans: The ordered pairs’ domain is the first component. Range, on the other hand, is the ordered pairs’ Second Component. If you find any duplicates, remove them. Domain \( = \{ 4,\,\, – 1,\,\,2,\,\,7,\,\,6\} \) Range \( = \{ 3,\,\,7,\,\, – 3,\,\,5,\,\, – 2\} \)
Q.3. From the following arrow diagram, find the domain and range and depict the relation between them.

Answer: We know that the domain is the set of the first element of the ordered pair. So, Domain \( = \{ 3,\,\,4,\,\,5\} \) And the range of a relation is the set of second elements of the ordered pair. Range \( = \{ 3,\,\,4,\,\,5,\,6\} \) From the given arrow diagram, we can write a relation \(R = \{ (3,\,\,4),\,(\,4,\,\,6),\,(5,\,3),(5,5)\} \)
Q.4. Determine the domain and range of the relation R defined by \(R = \{ x,\,\, – 2,\,\,2x + 3\} :\,x \in \{ 0,\,\,1,\,\,2,\,\,3,\,\,4,\,\,5\,\} \) Ans: Given \(x = \{ 0,\,\,1,\,\,2,\,\,3,\,\,4,\,\,5\} \) \(x = 0 \Rightarrow x – 2 = 0 – \,\,2 = \,\, – 2\) and \(2x + 3 = 2 \times 0 + 3 = 3\) \(x = 1 \Rightarrow x – 2 = 1 – \,\,2 = \,\, – 1\) and \(2x + 3 = 2 \times 1 + 3 = 5\) \(x = 2 \Rightarrow x – 2 = 2 – 2 = 0\) and \(2x + 3\, = 2 \times 2\, + 3\, = \,7\) \(x\, = 3\,\, \Rightarrow \,x\, – \,2\,\, = \,3 – \,2\, = 1\) and \(2x + 3 = \,2 \times 3 + 3\,\, = \,9\) \(x = \,4\, \Rightarrow \,x – 2\, = \,4 – 2\, = 2\) and \(2x + 3\, = 2 \times 4 + \,3\, = 11\) \(x\,\, = \,\,5\, \Rightarrow \,x – 2\, = \,5 – \,2\, = \,3\) and \(2x – \,3\, = 2 \times 5\, + 3\, = \,13\) Hence \(R = \,\{ – 2,\,\,3),\,( – 1,\,\,5)\,,\,(0,\,\,7)\,\,(1,\,\,9)\,(2,11)\,,\,(3,\,\,1\,3)\) Domain of \(R = \,\{ – 2,\, – 1,\,\,0,\,\,1,\,\,2,\,\,3\} \) Range of \(R\, = \,\{ 3,\,\,5,\,\,7\,,\,\,9,\,\,11,\,\,13\,\} \)
Q.5. A relationship between set \(X\) and set \(Y\) is depicted in the diagram below. Write the same thing in the roster and set builder Forms, and then figure out the domain and range.

Ans: In the set builder form \(R = \left\{ {\left( {x,\,y} \right):x\,{\rm{is}}\,{\rm{the}}\,{\rm{square}}\,{\rm{of}}\,y;\,x \in X,\,y \in Y} \right\}\) In roster form \(R = \{ (2,1)(4,\,\,2)\} \) Domain \( = \,\{ 2,\,4\} \) Range \( = \,\{ 1,\,\,2\} \)
In this article, we have discussed a relation and how to represent relations in three different forms, types of relations. Also, we discussed the domain and range of relations in detail, along with the solved examples and frequently asked questions.
Learn All the Concepts on Functions
Frequently Asked Questions: Domain and Range of Relation
Q.1. What is the domain for the relation? Ans: The domain of a relation is the set of the initial elements of all the ordered pairs of the relation.
Q.2. What is the range of a relation? Ans: The set of the second elements of all the ordered pairs of a relation is the range of a relation.
Q.3. What is the difference between relation and function? Ans: A relation is defined as a connection between two or more sets of values. It may also be thought of as a subset of the Cartesian product. A function is defined as a relationship in which each input has just one output. Every function is a relation, but not every relation is a function.
Q.4. What is the difference between domain and range? Ans: The domain of a function is all the values that go into it, and the range is all the values that come out of it in its simplest form. For a relation from \(A \to B\) all the elements of set \(A\) which are related to the elements of set \(B\) are the elements of the domain and all related elements of set \(B\) form the range.
Q.5. If a set \(A\) has n elements, and has m elements, what is the number of relations from \(A\,to\,B\) Ans: A relation from \(A\,to\,B\) is a subset of the Cartesian product \((A\, \times \,B)\) of two sets \(A\) and \(B\). There will be \((n\, \times \,m)\) elements \((A\, \times \,B)\) in if the set \(A\) has \(n\) elements and the set \(B\) has \(m\) elements. As a result, there will be \({2^{n\, \times \,m}}\) subsets \((A\, \times \,B)\) of and therefore \({2^{n\, \times \,m}}\) relations from \(A\,to\,B\) may be defined.
We hope this detailed article on the domain and range of relations helped you in your studies. If you have any doubts, queries or suggestions regarding this article, feel to ask us in the comment section and we will be more than happy to assist you. Happy learning!
Related Articles
Ways To Improve Learning Outcomes: With the development of technology, students may now rely on strategies to enhance learning outcomes. No matter how knowledgeable a...
Visual Learning Style: We as humans possess the power to remember those which we have caught visually in our memory and that too for a...
NCERT Books for Class 6 Social Science 2024: Many state education boards, including the CBSE, prescribe the NCRET curriculum for classes 1 to 12. Thus,...
CBSE Syllabus for Class 9 Social Science: The Central Board of Secondary Education releases the revised CBSE Class 9 Social Science syllabus. The syllabus is...
CBSE Syllabus for Class 8 Maths 2023-24: Students in CBSE Class 8 need to be thorough with their syllabus so that they can prepare for the...
NCERT Books for Class 6 Maths 2025: The National Council of Educational Research and Training (NCERT) textbooks are the prescribed set of books for schools...
CBSE Class 10 Study Timetable: The CBSE Class 10 is the board-level exam, and the Class 10th students will appear for the board examinations for...
CBSE Class 10 Syllabus 2025: The Central Board of Secondary Education (CBSE) conducts the Class 10 exams every year. Students in the CBSE 10th Class...
CBSE Syllabus for Class 11 2025: The Central Board of Secondary Education (CBSE) has published the Class 11 syllabus for all streams on its official...
NCERT Solutions for Class 7 Science Chapter 16 Water – A Precious Resource: In this chapter, students will study about the importance of water. There are three...
NCERT Solutions for Class 7 Science Chapter 10 2024: Respiration in Organisms
NCERT Solutions for Class 7 Science Chapter 10 Respiration in Organisms: NCERT solutions are great study resources that help students solve all the questions associated...
Factors Affecting Respiration: Definition, Diagrams with Examples
In plants, respiration can be regarded as the reversal of the photosynthetic process. Like photosynthesis, respiration involves gas exchange with the environment. Unlike photosynthesis, respiration...
NCERT Solutions for Class 7 Science Chapter 12
NCERT Solutions for Class 7 Science Chapter 12 Reproduction in Plants: The chapter 'Reproduction' in Class 7 Science discusses the different modes of reproduction in...
NCERT Solutions for Class 7 Science Chapter 11
NCERT Solutions for Class 7 Science Chapter 11: Chapter 11 of Class 7 Science deals with Transportation in Animals and Plants. Students need to ensure...
NCERT Solutions for Class 7 Science Chapter 15: Light
NCERT Solutions for Class 7 Science Chapter 15: The NCERT Class 7 Science Chapter 15 is Light. It is one of the most basic concepts. Students...
NCERT Solutions for Class 7 Science Chapter 13
NCERT Solutions for Class 7 Science Chapter 13: Chapter 13 in class 7 Science is Motion and Time. The chapter concepts have a profound impact...
NCERT Solutions for Class 7 Science Chapter 14: Electric Current and its Effects
NCERT Solutions for Class 7 Science Chapter 14: One of the most important chapters in CBSE Class 7 is Electric Current and its Effects. Using...
General Terms Related to Spherical Mirrors
General terms related to spherical mirrors: A mirror with the shape of a portion cut out of a spherical surface or substance is known as a...
Animal Cell: Definition, Diagram, Types of Animal Cells
Animal Cell: An animal cell is a eukaryotic cell with membrane-bound cell organelles without a cell wall. We all know that the cell is the fundamental...
NCERT Solutions for Class 10 Science 2024 – Download PDF
NCERT Solutions for Class 10 Science: The National Council of Educational Research and Training (NCERT) publishes NCERT Solutions for Class 10 Science as a comprehensive...
NCERT Books for Class 12 Chemistry 2024: Download PDF
NCERT Books for class 12 Chemistry: NCERT publishes chemistry class 12 books every year. The NCERT chemistry class 12 books are essential study material for...
CBSE Class 9 Mock Tests 2025: Attempt Online Mock Test Series (Subject-wise)
We all have heard at least once that the secret to success is practice. Some of you could say it's a cliché, but those who...
NCERT Books for Class 10 Maths 2025: Download Latest PDF
NCERT Books for Class 10 Maths: The NCERT Class 10 Maths Book is a comprehensive study resource for students preparing for their Class 10 board exams....
Arc of a Circle: Definition, Properties, and Examples
Arc of a circle: A circle is the set of all points in the plane that are a fixed distance called the radius from a fixed point...
CBSE Class 10 Mock Test 2025: Practice Latest Test Series
CBSE Class 10 Mock Test 2025: Students' stress is real due to the mounting pressure of scoring good marks and getting into a renowned college....
NCERT Solutions for Class 10 2024: Science and Maths
NCERT Solutions for Class 10 2024: Students appearing for the CBSE Class 10 board exam must go through NCERT Solutions to prepare for the exams...
NCERT Solutions for Class 12 2024 – Physics, Chemistry, Maths, Biology
NCERT Solutions for Class 12 2023-24: The NCERT Solutions for Class 12 are meant to help students understand what the subject holds. These solutions are...

39 Insightful Publications

Embibe Is A Global Innovator

Innovator Of The Year Education Forever

Interpretable And Explainable AI

Revolutionizing Education Forever

Best AI Platform For Education

Enabling Teachers Everywhere

Decoding Performance

Leading AI Powered Learning Solution Provider

Auto Generation Of Tests

Disrupting Education In India

Problem Sequencing Using DKT

Help Students Ace India's Toughest Exams

Best Education AI Platform

Unlocking AI Through Saas

Fixing Student’s Behaviour With Data Analytics

Leveraging Intelligence To Deliver Results

Brave New World Of Applied AI

You Can Score Higher

Harnessing AI In Education

Personalized Ed-tech With AI

Exciting AI Platform, Personalizing Education

Disruptor Award For Maximum Business Impact

Top 20 AI Influencers In India

Proud Owner Of 9 Patents

Innovation in AR/VR/MR

Best Animated Frames Award 2024
Trending Searches
Previous year question papers, sample papers.
Practice Domains & Relations Questions with Solutions & Ace Exam

Unlimited Practice Questions for Domains & Relations
Enter mobile number.
By signing up, you agree to our Privacy Policy and Terms & Conditions
- Avoiding Common Math Mistakes-Expanding
- Avoiding Common Math Mistakes-Trigonometry
- Avoiding Common Math Mistakes-Simplifiying
- Avoiding Common Math Mistakes-Square Roots
- Avoiding Common Math Mistakes-Working with negatives
- Complex Numbers
- Decimal and Percent
- Dosage Calculations
- Adding and Subtracting Fractions
- BEDMAS with Fractions
- Multiplying and Dividing Fractions
- Long Division
- Long Multiplication
- Order of Operations
- Calculating Slope Examples
- Graphs of Functions
- Least Squares Trendline and Correlation
- Semi-Log and Log-Log Graphs
- Pythagorean Theorem
- Ratio and Proportion
- Rounding and Significant Figures
- Scientific Notation
- Square Root
- Unit Conversion for the Sciences
- Unit Conversion Examples
- Application of Derivatives: Examples
- Chain Rule: Examples
- Higher Order Derivatives: Examples
- Power Rule: Example
- Product Rule: Examples
- Quotient Rule: Examples
- Fundamental Theorem of Calculus
- Net Change Theorem: Example
- Newton's Method
- Completing the Square
- Simplifying Expressions
- Absolute Value Equations
- The Quadratic Formula
- Rational Equations
- Solving Equations: Application
- Solving Linear Equations
- Solving Linear Inequalities
- Solving Linear Systems
- Word Problems
- Domain and Range of Exponential and Logarithmic Functions
- Transformation of Exponential and Logarithmic Functions
- Solving Exponential and Logarithmic Equations
- Logarithmic Models
- Composition of Functions
Domain and Range Examples
- Domain and Range Exponential and Logarithmic Fuctions
- Domain and Range of Trigonometric Functions
- Evaluating Functions
- One-to-One and Onto Functions
- Inverse Functions
- Equations of Lines
- Setting Up Linear Models
- Piecewise-Defined Functions
- Transformations of Exponential and Logarithmic Functions
- Transformations of Trigonometric Functions
- Bar Graph and Pie Chart
- Linear Regression and Correlation
- Normal Distribution
- Standard Deviation
- Avoiding Common Math Mistakes in Trigonometry
- Solving Trigonometric Equations
- Trigonometry on the Unit Circle
- Introduction to Trigonometric Functions
- Inverse Trigonometric Functions
- Setting Up Trigonometric Models
- Vector Magnitude, Direction, and Components
- Angle Between Vectors
- Vector Addition, Subtraction, and Scalar Multiplication
- Vector Dot Product and Cross Product
- Matrix Addition, Subtraction, and Multiplication by a Scalar
- Matrix Multiplication
- Special Matrices and Definitions
- How do I use my scientific calculator?
- How do I approach word problems?
- I got the right answer, so why didn't I get full marks?
- Open Educational Resources
- Balancing equations
- Chemical bonding
- Lewis Structures
- Periodic table
- Significant figures
- Stoichiometry
- The Clausius-Clapeyron equation
- Yield calculations
- Assignment Planning Calculator
- Grammar Resources
- Misused Modifiers
- Overview of future times
- Overview of past tenses
- Overview of present tenses
- Overview of verb tenses and APA recommendations for tense usage in academic writing
- Parallel Structure
- Pronoun Usage
- Run-on Sentences
- Sentence Fragments
- Sentence Structure: Prepositional Phrases
- Slang and Colloquial Language
- The Important Joining Words
- Word Classes, Prefixes and Suffixes
- Wordiness: Using more words than is necessary
- Words Frequently Misused
- Apostrophe Usage
- Capitalization
- Comma Splice
- How to use a semi-colon
- Pronunciation Resources
- Words that sound similar
- Vocabulary Resources
- Research proposals
- Writing a review of literature
- Accessing Citation Guides at the Ontario Tech University Library
- Avoiding Plagiarism
- What is Turnitin.com?
- About Documenting Your Work
- American Chemical Society (ACS) Citations
- American Institute of Physics (AIP) Citations
- APA 7th Edition: Formatting
- APA 7th Edition: Sample Student Paper
- APA 7th Edition: Paper Checklist
- American Psychological Association (APA) 7th Edition: Tables and Figures
- APA 7th Edition: In-text Citations
- APA 7th Edition: Referencing
- APA 7th Edition: Common Errors in Citation
- The Chicago Manual of Style (CMOS): Notes
- The Chicago Manual of Style (CMOS): Bibliography
- CMOS Quick Reference Guide
- Council of Science Editors
- McGill Guide: Footnotes
- MLA: Quick Reference Guide 8th Edition
- Vancouver Style
- Example IEEE References
- Assignment Comprehension
- Developing a Thesis Statement
- Essay Outline
- Primary Data Collection
- Wikipedia and Google Scholar
- Finding Sources
- How to Find Articles Using Google Scholar
- How to Find Books on the Library Website
- OMNI Searches
- Types of Source
- Body Paragraph Structure
- Introductions and Conclusions
- Patterns of Organization
- When Researching, Keep Track of the Following
- Incorporating Sources into your Writing
- Paraphrasing
- Summarizing
- Integrating Technical Writing
- Helpful Resources
- Why Revise?
- How Do I Revise?
- Switching from Writer to Reader
- Incorrect Prefixes and Suffixes
- Missing Words
- Pronoun Errors
- Subject-Verb Agreement
- Frequently Misused Words
- Proofreading
- Descriptive abstracts
- Informative abstracts
- American National Standard for writing abstracts
- APA 7th abstracts
- Conference abstracts
- Engineering abstracts
- Five-part abstracts
- What Causes Writer's Block?
- Strategies to Overcome Writer's Block
- Annotated Bibliography
- Article/Journal Reviews
- Business and Professional Communication
- Business Plans
- Case Studies
- Laboratory Reports
- Literature Review
- Presentations
- Primary/Field Research
- Progress Reports
- Project Proposals
- Reflective Progress Notes
- Research Paper
- Scientific Manuscript By Dr. Chris Garside
- Scientific Manuscript By Sylvie Bardin
- Standards of Practice Project
- Thesis and Capstone Projects
- Business Financial Database Tutorial
- Business Terms
- A Short Guide to Annotated Bibliographies
- Writing about Indigenous Peoples
- Quick exam tips
- Exam preparation self-assessment
- Regular review
- Planning tools
- Figuring out what to study
- Staying calm before the test
- Essay questions
- Multiple-choice questions
- Problem-solving and math questions
- Short and long answer questions
- Exam preparation resources
- Calculate your course grade
- How Do We Divide Tasks?
- How to Get Started
- Self-Assessment
- Optimize Your Study Session
- Active Study Strategies
- Recall Techniques
- Problem Solving, Experiential Learning, and Critical Thinking
- Online Learning
- Organizational Tools
- Procrastination, Burnout, and Motivation
- Concept Maps
- Studying for Math
- Evernote Tutorials: Note-taking and Organization tool
- Study Blue Tutorial: Note-taking and Flashcard Tool
- Mathematics
- Domain and Range

- School Guide
- Mathematics
- Number System and Arithmetic
- Trigonometry
- Probability
- Mensuration
- Maths Formulas
- Class 8 Maths Notes
- Class 9 Maths Notes
- Class 10 Maths Notes
- Class 11 Maths Notes
- Class 12 Maths Notes
Domain and Range for Graph
Domain and Range are fundamental in understanding the behavior of functions when they are represented graphically. Domain of a function refers to all the possible input values (typically represented on the x-axis) that the function can accept without resulting in any undefined behavior. On the other hand, the range is the set of all possible output values (typically shown on the y-axis) that the function can produce.
In this article, we will discuss all things related to Domain and Range for Graph
Domain and Range
Domain and range of any particular function are fundamental concepts to understand about functions in mathematics, and especially when dealing with graphs of functions. The domain of a function can be defined as set of all possible x-values that can be taken by the function while the range can be defined as set of all possible y-values that can be taken by the function.
While this idea may not have direct applications in daily life, it is important for students because based on this concept, functions may be analyzed or interpreted in numerous fields like physics, engineering, economics and others.
What is the Domain?
The domain of a function is the complete set of possible values of the independent variable, which are typically the x-values.
How to Find the Domain from a Graph?
Finding the domain of a function from its graph involves identifying all the possible input values (x-values) for which the function is defined. Here’s a step-by-step approach:
Step 1: Look at the range of x-values over which the function exists. Step 2: Check if there are any breaks, holes, or vertical asymptotes in the graph. These indicate x-values where the function is not defined. Step 3: For graphs with endpoints (e.g., closed intervals), include these x-values if they are part of the domain. Step 4: For functions that extend infinitely, determine if the domain extends to positive or negative infinity. Step 5: Write the domain in interval notation, set-builder notation, or as a union of intervals, depending on the graph’s characteristics.
Example for Domain
- Linear Function: For f(x) = 2x + 3 the graph is a straight line extending infinitely in both direction hence the set of all real numbers is included in the domain which is (-∞, ∞).
- Square Root Function: If f(x) = x, The begin at x=0 on the number line and goes on to the right. It follows that for the domain of the variable x, it means it is greater than equal to 0, that is [0, ∞).
What is the Range?
Range refers to the set of all possible output values (or y -values) that a function can produce. In other words, it is the set of all values that the function maps to from the domain (the set of input values or x -values).
To find the range of a function, you consider all possible values that the function can take as you vary the input values over the domain.
For a simple linear function like f(x) = 2x + 3, where x can be any real number:
- The range is also all real numbers because, as x varies, f(x) can take any real value.
How to Find the Range from a Graph?
Finding the range of a function from its graph involves identifying the set of all possible output values (y-values) that the function takes. Here are the steps for the same:
Step 1: Look at the lowest point and the highest point that the graph reaches along the y-axis. These points represent the minimum and maximum values that the function attains (if they exist). Step 2: Check if the graph extends indefinitely in the vertical direction. For example, if the graph continues to rise or fall without bound, then the range will be all real numbers (for instance, −∞ to ∞). Step 3: For a graph that opens upward or downward (like a parabola), the range might start from the vertex and extend infinitely in one direction. For periodic functions like sine or cosine, the graph repeats in a regular pattern, and the range is determined by the highest and lowest points in one cycle. Step 4: If there are any gaps in the graph (e.g., a function with asymptotes or holes), then those y-values are excluded from the range. Step 5: Based on your observations, express the range. Use interval notation if possible: If the function has a minimum value a and no maximum, the range might be [a,∞). If it has both a minimum and maximum, the range could be [a, b]. If the graph covers all possible y-values, the range is (−∞,∞).
Examples of Range
- Quadratic Function: If the function is f(x) = x 2 , the graph formed is a parabola, which is a up- ward opening parabola with minimum value of y = 0. As such, the interval of values is the set of all non-negative, infinitive numbers, or [0, ∞).
- Trigonometric Function (Sine): This is because the absolute largest value a sine function may reach is 1 and the absolute minimum value is -1 due to the nature of the sine function; from period to period, the graph go up to 1 and down to -1 giving the range [−1, 1].
Graphical Representation of Domain and Range
To graphically represent the domain and range of a function, you typically follow these steps:
- First, you need to plot the function on a coordinate plane.
- Domain of a function consists of all the possible input values (x-values) for which the function is defined.
- Range of a function consists of all the possible output values (y-values) that the function can produce.
Visualizing Domain on the X-Axis
To visualize a domain on the x-axis, typically in a graph or plot, the x-axis represents the domain values, while the y-axis represents the range (the corresponding output values).
Visualizing Range on the Y-Axis
To visualize a range on the y-axis, typically in a graph or plot, the y-axis represents the range values, while the x-axis represents the domain (the corresponding input values).
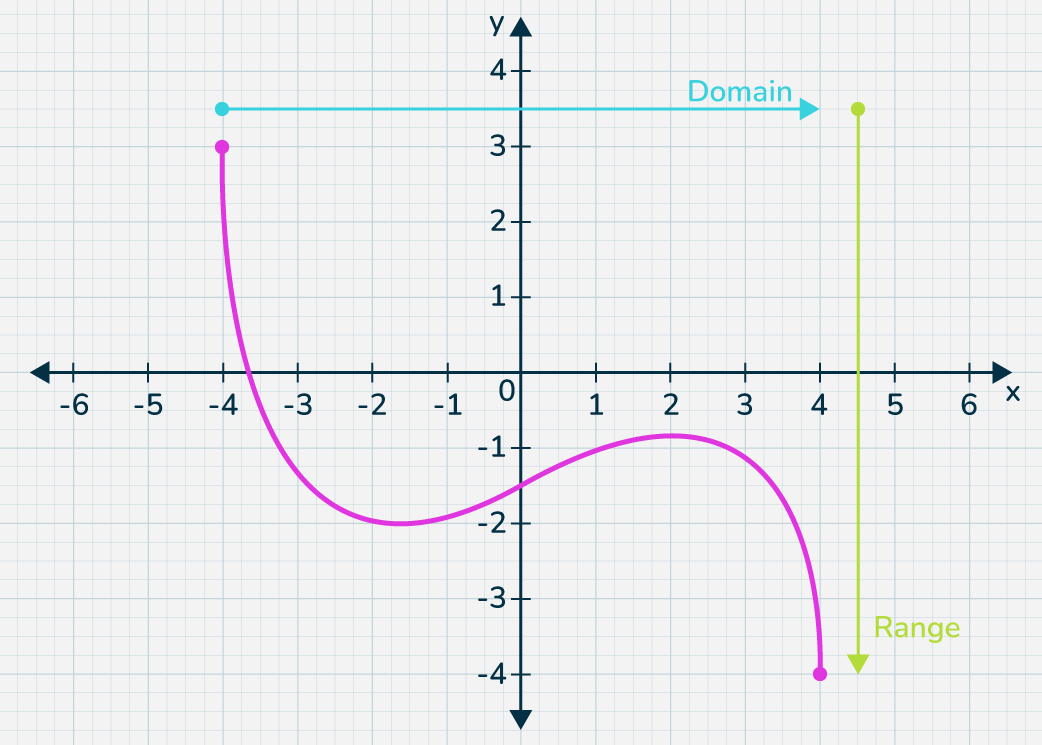
- Domain and Range of Function
- Range of a Function
- Domain and Range of a Relation
- Difference between Codomain and Range
Solved Problems: Domain and Range
Problem 1: Find the domain and range of the function f(x) = 1/x-2 .
Domain : The function is undefined when x equals 2 so the domain of this sil is negative infinity and 2 union two and infinity. Range : Since the function can take any value other than zero, the values of the function at x = 0 are excluded, thus the range is minus ‘∞’ and plus ‘∞’.
Problem 2: Determine the domain and range of f(x) = (4−x 2 ) 1/2
Domain : The expression under the square root must be non-negative so that 4- x^2 ≥ 0. Solving −2 ≤ x ≤ 2 the domain is [−2, 2]. Range : This in turn equals to 2 only when x = 0 then greater than 0 to equal 0 when x = ±2 as so make the interval of the range from 0 up to 2.
Problem 3: Determine the domain and range of the function f(x) = x² + 3x + 2.
Domain : The function f(x) = x² + 3x + 2 is quadratic and it has all the characteristics similar to the quadratic polynomial f(x)=ax²+bx+c whereby ?=1, ?=3 & ?=2 The function is defined for all real numbers. Thus, its domain is all the real numbers, which are indicated by the interval from negative infinity to positive infinity. Range : To find the range we begin with the vertex of the parabola because it is the lowest or highest point about which the function opens. The vertex form of a quadratic function of the form ?x² + ?x + ? is x = −?/(2?). For f(x) = x 2 + 3x + 2, we calculate: x = k/n = -3/(2 × 1) = -3/2. Next, we substitute x = −3/2 into the function to find the minimum value: f(−3/2) = (−3/2)² + 3(−3/2) + 2 = 9/4 − 9/2 + 2 = 1/4. From the fact that the parabola opens upward, we know that range is [1/4, ∞).
Problem 4: Identify the domain and range of the function f(x) = 9 − x².
Domain : The definition of the function f(x) = 9 − x² is when the following is true: √(9−x²) becomes real, or in other words 9−x² ≥ 0. This leads to x² ≤ 9 or in other words -3 ≤ x ≤ 3. Hence, the domain of is [−3, 3]. Range : The function f(x) = 9 − x² is the graph of the upper half of a circle with radius 3 centred at the origin. It has a minimum value of 0 at x=3 or x=-3 and a maximum value of 3 at x=0. Thus range is [0, 3].
Problem 5: Identify the domain and range of the function f(x) = ?^x + 2.
Domain : The exponential function ?^x is defined for all real numbers so the domain of the function f(x) = ?^x + 2 is also (−∞, ∞. Range : The smallest value which ?^x can attain is 0 and this is attained as x moves closer to negative infinity. As such the minimum value of ?(x)= 2 and as the value of x increases the value of ?(x) increases without any upper limit. Hence the range is (2, infinity).
Problem 6: Determine the domain and range of the function f(x) = 2x^2 + 1.
Domain : The function f(x) = 2x^2 + 1 can be defined for all the real numbers which makes the domain as (∞, ∞). Range : The fundamental of x^2 + 1 is 1 and this is achieved when x = 0. When x^2 increases, the function increases without bound and, therefore the range is [1, ∞).
Problem 7: Find the domain and range of the function f(x) = sin(x) + 1.
Domain : The given function f(x) = sin(x) + 1 is valid for all the real values of x so the domain of this function is (-∞ ∞). Range : The sine function ranges between -1 and 1 and thus f(x) ranges between 0 and 2. Hence, the range is as follows: [0,2].
Problem 8: Identify the domain and range of the function f(x) = |x − 2|.
Domain: The function f(x) = |x − 2| is defined for all real numbers, so the domain is (−∞, ∞). Range: The absolute value function ∣x−2∣ is always non-negative and reaches its minimum value of 0 when x = 2. Therefore, the range is [0,∞).
Problem 9: Identify the domain and range of f(x)=tan(x)
Domain: The function f(x)=tan(x) is undefined when cos(x)=0, which occurs at x = π/2 + nπ, where n is an integer. Therefore, the domain is: x∈R∖{π/2 + nπ ∣ n∈Z} Range: The tangent function can take any real value, so the range is (−∞,∞).
Problem 10: Find the domain and range of f(x) = 1/x-1 for x ≥ 0
Domain: The function f(x) = 1/x-1 is undefined when x = 1. Given that x ≥ 0, the domain is: [0, 1) ∪ (1, ∞) Range: As x approaches 1 from the left, f(x) approaches −∞, and as x approaches 1 from the right, f(x) approaches ∞. Therefore, the range is (−∞, 0) ∪ (0, ∞).
Domain and Range: Practice Problems
Instructions: Identify the domain and range for the following functions.
Problem 1: f(x) = x² – 4x + 4
Problem 2: f(x) = 3/(x + 2)
Problem 3: f(x) = (25 – x 2 ) 1/2
Problem 4: f(x) = log(x + 5)
Problem 5: f(x) = e 2x
Problem 6: f(x) = sin(2x)
Problem 7: f(x) = |x – 3| + 2
Problem 8: f(x) = cos(x) – 1
Problem 9: f(x) = 1/(x 2 – 1)
Problem 10: f(x) = (x – 1) 1/2
Answer Key:
1: Domain: (-∞, ∞), Range: [0, ∞)
2: Domain: (-∞, -2) ∪ (-2, ∞), Range: (-∞, 0) ∪ (0, ∞)
3: Domain: [-5, 5], Range: [0, 5]
4: Domain: (-5, ∞), Range: (-∞, ∞)
5: Domain: (-∞, ∞), Range: (0, ∞)
6: Domain: (-∞, ∞), Range: [-1, 1]
7: Domain: (-∞, ∞), Range: [2, ∞)
8: Domain: (-∞, ∞), Range: [-2, 0]
9: Domain: (-∞, -1) ∪ (-1, 1) ∪ (1, ∞), Range: (-∞, 0) ∪ (0, ∞)
10: Domain: [1, ∞), Range: [0, ∞)
What is the domain and range of a function?
Domain is the collection of all elements of interest (the independent variable x) and the range is the collection of all the possible corresponding elements of interest (the dependent variable y).
How can I find the domain of a function?
To find the range, identify the y-values that the function attains and stay way from values that result in undecidedness such as division by zero and values less than 0 under a square root.
How do I determine the range of a function from a graph?
To notice the range look specifically at the lowest and the highest point marked on the graph’s y-axis.
Can a function have an infinite range?
Yes, for instance, straight lines such as identity function f(x) = x have a range of: (–∞, ∞).
What is the domain of a logarithmic function?
The domain of a logarithmic function f(x) = log(x) is (0,∞) because logarithm is not defined in case of non-positive values of x.
Why is understanding domain and range important?
About the domain and range, it is very important in the actual interpretation and analysis of functions which are fundamental in many mathematical applications.
Are there functions with the same domain but different ranges?
Yes, a function can share the same domain but the range different based on how the output values are set.
Please Login to comment...
Similar reads.
- School Learning
- Relations and Functions
- How to Get a Free SSL Certificate
- Best SSL Certificates Provider in India
- Elon Musk's xAI releases Grok-2 AI assistant
- What is OpenAI SearchGPT? How it works and How to Get it?
- Content Improvement League 2024: From Good To A Great Article
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
- AI Math Solver Graphing Calculator Popular Problems Worksheets Study Guides Cheat Sheets Calculators Verify Solution
- Solutions Integral Calculator Derivative Calculator Algebra Calculator Matrix Calculator More...
- Graphing Line Graph Exponential Graph Quadratic Graph Sine Graph More...
- Calculators BMI Calculator Compound Interest Calculator Percentage Calculator Acceleration Calculator More...
- Geometry Pythagorean Theorem Calculator Circle Area Calculator Isosceles Triangle Calculator Triangles Calculator More...
- Tools Notebook Groups Cheat Sheets Worksheets Study Guides Practice Verify Solution
| x^{\msquare} | \log_{\msquare} | \sqrt{\square} | \nthroot[\msquare]{\square} | \le | \ge | \frac{\msquare}{\msquare} | \cdot | \div | x^{\circ} | \pi | |||||||||||
| \left(\square\right)^{'} | \frac{d}{dx} | \frac{\partial}{\partial x} | \int | \int_{\msquare}^{\msquare} | \lim | \sum | \infty | \theta | (f\:\circ\:g) | f(x) | |||||||||||
| ▭\:\longdivision{▭} | \times \twostack{▭}{▭} | + \twostack{▭}{▭} | - \twostack{▭}{▭} | \left( | \right) | \times | \square\frac{\square}{\square} |
- Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
- Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Prove That Logical Sets Word Problems
- Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Coterminal Angle Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
- Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
- Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
- Linear Algebra Matrices Vectors
- Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
- Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
- Physics Mechanics
- Chemistry Chemical Reactions Chemical Properties
- Finance Simple Interest Compound Interest Present Value Future Value
- Economics Point of Diminishing Return
- Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
- Pre Algebra
- Pre Calculus
- Given Points
- Given Slope & Point
- Slope Intercept Form
- Start Point
- Parallel Lines
- Perpendicular
- Perpendicular Lines
- Perpendicular Slope
- Is a Function
- Domain & Range
- Slope & Intercepts
- Periodicity
- Domain of Inverse
- Critical Points
- Inflection Points
- Monotone Intervals
- Extreme Points
- Global Extreme Points
- Absolute Extreme
- Turning Points
- End Behavior
- Average Rate of Change
- Piecewise Functions
- Discontinuity
- Values Table
- Compositions
- Arithmetics
- Circumference
- Eccentricity
- Conic Inequalities
- Transformation
- Linear Algebra
- Trigonometry
- Conversions
| x^{\msquare} | \log_{\msquare} | \sqrt{\square} | \nthroot[\msquare]{\square} | \le | \ge | \frac{\msquare}{\msquare} | \cdot | \div | x^{\circ} | \pi | |||||||||||
| \left(\square\right)^{'} | \frac{d}{dx} | \frac{\partial}{\partial x} | \int | \int_{\msquare}^{\msquare} | \lim | \sum | \infty | \theta | (f\:\circ\:g) | f(x) | |||||||||||
| - \twostack{▭}{▭} | \lt | 7 | 8 | 9 | \div | AC |
| + \twostack{▭}{▭} | \gt | 4 | 5 | 6 | \times | \square\frac{\square}{\square} |
| \times \twostack{▭}{▭} | \left( | 1 | 2 | 3 | - | x |
| ▭\:\longdivision{▭} | \right) | . | 0 | = | + | y |
Number Line
- domain\:and\:range\:y=\frac{x^2+x+1}{x}
- domain\:and\:range\:f(x)=x^3
- domain\:and\:range\:f(x)=\ln (x-5)
- domain\:and\:range\:f(x)=\frac{1}{x^2}
- domain\:and\:range\:y=\frac{x}{x^2-6x+8}
- domain\:and\:range\:f(x)=\sqrt{x+3}
- domain\:and\:range\:f(x)=\cos(2x+5)
- domain\:and\:range\:f(x)=\sin(3x)
function-domain-and-range-calculator
- Functions A function basically relates an input to an output, there’s an input, a relationship and an output. For every input...
We want your feedback
Please add a message.
Message received. Thanks for the feedback.
:quality(80):no_upscale()/https://images.domain.com.au/img/20589/contact_1956610.jpeg?date=638604029654630000)
- Virtual Tour
31 Range View Way, High Wycombe WA 6057
- Available from Tuesday, 10th September 2024
Property Features
* Unverified feature
- Built in wardrobes*
- Split System AC
- Outdoor Entertaining
Property Description
Space for all the family.
3 good size bedrooms all with BIRS. Plus Sleepout/Study. Formal Lounge. Open Plan Kitchen/Meals. Big Open plan Family. Split System Air conditioners. Outdoor Entertaining Patio. 3/4 Car Lockup Carport with Remote
Please register online for the inspection.
Disclaimer: All information contained therein is gathered from relevant third parties sources. We cannot guarantee or give any warranty about
Domain Says
First listed on 27 August, this house has been on Domain for 1 day (last updated on 27 August). 124 other 3 bedroom house in High Wycombe have recently been sold.
- Street View
Inspection times
Inspections, want to visit this property.
Contact agent to organise an inspection time.
Can't inspect in person?
Contact the agent to request a personal walkthrough of the property over video call.
School Catchment Zones for 31 Range View Way
Government school catchment, edney primary school.
0.7 km away
Darling Range Sports College
3.8 km away
Kalamunda Senior High School
6.1 km away
Neighbourhood Insights
A little bit about who lives locally, as provided by government census data.
| Age | % |
|---|---|
| under 20 | |
| 20 - 39 | |
| 40 - 59 | |
| 60+ |
Street Profile
Recently rented, owner/renter:, insights for 3 bedroom houses in high wycombe, market performance, median price : , auction clearance : , sold this year : , avg days on market : , demographics, population : , occupancy: , average age : , household: , people who viewed this property also viewed....
121A Hale Road Forrestfield
9 Hove Court Forrestfield
11 Newburn Road High Wycombe
62 Palmer Crescent High Wycombe
26 Newburn Road High Wycombe
521A Kalamunda Road High Wycombe
29 Barbary Road High Wycombe
1A Bailey Road Lesmurdie
13 Hibiscus Drive Forrestfield
13A Hulley Road High Wycombe
2/19 Cumberland Road Forrestfield
22 Tarata Way Forrestfield
5/18 Brooks Street Kalamunda
6 Annato Place Forrestfield
9 Carleton Crescent Forrestfield
15 Silver Princess Way Jane Brook
3 Dagenham Crescent Midvale
46/1 Balfour Road Swan View
83 Waldeck Road Caversham
Property FAQs
What is the weekly rent for 31 range view way, high wycombe, when is 31 range view way, high wycombe available to rent, how much is the rental bond for 31 range view way, high wycombe, how many bedrooms does 31 range view way, high wycombe have, what are the key property features of 31 range view way, high wycombe, what is the size of the property at 31 range view way, high wycombe, how many car spaces does 31 range view way, high wycombe have.

IMAGES
COMMENTS
F i g. 1 A function maps every element in the domain to exactly one element in the range. Although each input can be sent to only one output, two different inputs can be sent to the same output. We can also visualize a function by plotting points (x,y) in the coordinate plane where y=f(x). The graph of a function is the set of all these points.
For the cube root function \(f(x)=\sqrt[3]{x}\), the domain and range include all real numbers. Note that there is no problem taking a cube root, or any odd-integer root, of a negative number, and the resulting output is negative (it is an odd function). Given the formula for a function, determine the domain and range.
Example #1: Find the Domain and Range of a Graph. For our first example, we are given the graph of the function f (x)=x^2 and we are tasked with finding the domain and the range (note that our answers must be in interval notation). Figure 08: Find the domain and range of the graph of y=x^2.
For example, find the range of 3x 2 + 6x -2. Calculate x-coordinate of vertex: x = -b/2a = -6/ (2*3) = -1. 3. Calculate the y-value of the vertex of the function. Plug the x-coordinate into the function to calculate the corresponding y-value of the vertex. This y-value denotes the edge of your range for the function.
Example 5. Find the domain and range of the following function. f (x) = 2/ (x + 1) Solution. Set the denominator equal to zero and solve for x. x + 1 = 0. = -1. Since the function is undefined when x = -1, the domain is all real numbers except -1. Similarly, the range is all real numbers except 0.
A domain of a function refers to "all the values" that can go into a function without resulting in undefined values. i.e., The domain in math is the set of all possible inputs for the function. Consider the above box as a function f(x) = 2x.Inputting the values x = {1,2,3,4,...}, the domain is simply the set of natural numbers.
Domain and range. The domain and range of a function is all the possible values of the independent variable, x, for which y is defined. The range of a function is all the possible values of the dependent variable y.In other words, the domain is the set of values that we can plug into a function that will result in a real y-value; the range is the set of values that the function takes on as a ...
Both the domain and range are the set of all real numbers. Figure 3.3.14: Absolute function f(x) = | x |. For the absolute value function f(x) = | x |, there is no restriction on x. However, because absolute value is defined as a distance from 0, the output can only be greater than or equal to 0.
Finding Domain and Range from Graphs. Another way to identify the domain and range of functions is by using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values, which are shown on the y-axis. Keep in mind ...
Domain. The domain of a function is the complete set of possible values of the independent variable. In plain English, this definition means: The domain is the set of all possible x -values which will make the function "work", and will output real y -values. When finding the domain, remember: The denominator (bottom) of a fraction cannot be zero.
Another way to identify the domain and range of functions is by using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x -axis. The range is the set of possible output values, which are shown on the y -axis.
Yet, we can still determine the domain and range of this relation. Recall, the domain is the set of all x-values. Here are the x-values in set H. Domain = {-2, -1, 0, 1, 2} Take care to notice that two '1's were not listed because it is unnecessary to duplicate domain values. Those five values are the only x-values that set H takes on. To ...
A function, by definition, can only have one output value for any input value. So this is one of the few times your Dad may be incorrect. A circle can be defined by an equation, but the equation is not a function. But a circle can be graphed by two functions on the same graph. y=√ (r²-x²) and y=-√ (r²-x²)
The domain is defined as the entire set of values possible for independent variables. The Range is found after substituting the possible x- values to find the y-values. Solved Examples. Example 1: Find the domain and range of a function f(x) = 3x 2 - 5. Solution: Given function: f(x) = 3x 2 - 5
The Codomain is actually part of the definition of the function. And The Range is the set of values that actually do come out. Example: we can define a function f (x)=2x with a domain and codomain of integers (because we say so). But by thinking about it we can see that the range (actual output values) is just the even integers.
The domain of a function f ( x ) is the set of all values for which the function is defined, and the range of the function is the set of all values that f takes. (In grammar school, you probably called the domain the replacement set and the range the solution set. They may also have been called the input and output of the function.)
Home. Domain and Range of Exponential and Logarithmic Functions. Recall that the domain of a function is the set of input or x -values for which the function is defined, while the range is the set of all the output or y -values that the function takes. A simple exponential function like f ( x ) = 2 x has as its domain the whole real line.
Domain and Range of Relation: A relation is a rule that connects elements in one set to those in another. \(A\) and \(B\) If are non-empty sets, then the relationship is a subset of Cartesian Product \(A \times B\). The domain is the set of initial members of all ordered pairs.
Domain & Range---The Easy Way First, let's start off with a little definition of each term so we can hopefully begin to understand these concepts a little better. A function is a relation from a domain set to a range set, where each element of the domain set is related to exactly one element of the range set.
2000 Simcoe Street North Oshawa, Ontario L1G 0C5 Canada. 905.721.8668. Ontario Tech University is the brand name used to refer to the University of Ontario Institute of Technology.
Domain and Range are fundamental in understanding the behavior of functions when they are represented graphically. Domain of a function refers to all the possible input values (typically represented on the x-axis) that the function can accept without resulting in any undefined behavior. On the other hand, the range is the set of all possible output values (typically shown on the y-axis) that ...
These cookies and other technologies allow us to understand how you interact with our Service (e.g., how often you use our Service, where you are accessing the Service from and the content that you're interacting with).
Free functions domain and range calculator - find functions domain and range step-by-step
4 bedroom house for Sale at 2/1 Rifle Range Road, Bligh Park NSW 2756. View property photos, floor plans, local school catchments & lots more on Domain.com.au. 2019450055
View this 3 bedroom, 1 bathroom rental house at 31 Range View Way, High Wycombe WA 6057. Available from Tuesday, 10 September 2024. Contact agent for price.