null hypothesis example p value

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base
• Understanding P values | Definition and Examples

Understanding P-values | Definition and Examples

Published on July 16, 2020 by Rebecca Bevans . Revised on June 22, 2023.

The p value is a number, calculated from a statistical test, that describes how likely you are to have found a particular set of observations if the null hypothesis were true.

P values are used in hypothesis testing to help decide whether to reject the null hypothesis. The smaller the p value, the more likely you are to reject the null hypothesis.

Table of contents

What is a null hypothesis, what exactly is a p value, how do you calculate the p value, p values and statistical significance, reporting p values, caution when using p values, other interesting articles, frequently asked questions about p-values.

All statistical tests have a null hypothesis. For most tests, the null hypothesis is that there is no relationship between your variables of interest or that there is no difference among groups.

For example, in a two-tailed t test , the null hypothesis is that the difference between two groups is zero.

• Null hypothesis ( H 0 ): there is no difference in longevity between the two groups.
• Alternative hypothesis ( H A or H 1 ): there is a difference in longevity between the two groups.

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

The p value , or probability value, tells you how likely it is that your data could have occurred under the null hypothesis. It does this by calculating the likelihood of your test statistic , which is the number calculated by a statistical test using your data.

The p value tells you how often you would expect to see a test statistic as extreme or more extreme than the one calculated by your statistical test if the null hypothesis of that test was true. The p value gets smaller as the test statistic calculated from your data gets further away from the range of test statistics predicted by the null hypothesis.

The p value is a proportion: if your p value is 0.05, that means that 5% of the time you would see a test statistic at least as extreme as the one you found if the null hypothesis was true.

P values are usually automatically calculated by your statistical program (R, SPSS, etc.).

You can also find tables for estimating the p value of your test statistic online. These tables show, based on the test statistic and degrees of freedom (number of observations minus number of independent variables) of your test, how frequently you would expect to see that test statistic under the null hypothesis.

The calculation of the p value depends on the statistical test you are using to test your hypothesis :

• Different statistical tests have different assumptions and generate different test statistics. You should choose the statistical test that best fits your data and matches the effect or relationship you want to test.
• The number of independent variables you include in your test changes how large or small the test statistic needs to be to generate the same p value.

No matter what test you use, the p value always describes the same thing: how often you can expect to see a test statistic as extreme or more extreme than the one calculated from your test.

P values are most often used by researchers to say whether a certain pattern they have measured is statistically significant.

Statistical significance is another way of saying that the p value of a statistical test is small enough to reject the null hypothesis of the test.

How small is small enough? The most common threshold is p < 0.05; that is, when you would expect to find a test statistic as extreme as the one calculated by your test only 5% of the time. But the threshold depends on your field of study – some fields prefer thresholds of 0.01, or even 0.001.

The threshold value for determining statistical significance is also known as the alpha value.

Receive feedback on language, structure, and formatting

Professional editors proofread and edit your paper by focusing on:

• Academic style
• Vague sentences
• Style consistency

See an example

P values of statistical tests are usually reported in the results section of a research paper , along with the key information needed for readers to put the p values in context – for example, correlation coefficient in a linear regression , or the average difference between treatment groups in a t -test.

P values are often interpreted as your risk of rejecting the null hypothesis of your test when the null hypothesis is actually true.

In reality, the risk of rejecting the null hypothesis is often higher than the p value, especially when looking at a single study or when using small sample sizes. This is because the smaller your frame of reference, the greater the chance that you stumble across a statistically significant pattern completely by accident.

P values are also often interpreted as supporting or refuting the alternative hypothesis. This is not the case. The  p value can only tell you whether or not the null hypothesis is supported. It cannot tell you whether your alternative hypothesis is true, or why.

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Normal distribution
• Descriptive statistics
• Measures of central tendency
• Correlation coefficient
• Null hypothesis

Methodology

• Cluster sampling
• Stratified sampling
• Types of interviews
• Cohort study
• Thematic analysis

Research bias

• Implicit bias
• Cognitive bias
• Survivorship bias
• Availability heuristic
• Nonresponse bias
• Regression to the mean

A p -value , or probability value, is a number describing how likely it is that your data would have occurred under the null hypothesis of your statistical test .

P -values are usually automatically calculated by the program you use to perform your statistical test. They can also be estimated using p -value tables for the relevant test statistic .

P -values are calculated from the null distribution of the test statistic. They tell you how often a test statistic is expected to occur under the null hypothesis of the statistical test, based on where it falls in the null distribution.

If the test statistic is far from the mean of the null distribution, then the p -value will be small, showing that the test statistic is not likely to have occurred under the null hypothesis.

Statistical significance is a term used by researchers to state that it is unlikely their observations could have occurred under the null hypothesis of a statistical test . Significance is usually denoted by a p -value , or probability value.

Statistical significance is arbitrary – it depends on the threshold, or alpha value, chosen by the researcher. The most common threshold is p < 0.05, which means that the data is likely to occur less than 5% of the time under the null hypothesis .

When the p -value falls below the chosen alpha value, then we say the result of the test is statistically significant.

No. The p -value only tells you how likely the data you have observed is to have occurred under the null hypothesis .

If the p -value is below your threshold of significance (typically p < 0.05), then you can reject the null hypothesis, but this does not necessarily mean that your alternative hypothesis is true.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bevans, R. (2023, June 22). Understanding P-values | Definition and Examples. Scribbr. Retrieved August 22, 2024, from https://www.scribbr.com/statistics/p-value/

Is this article helpful?

Rebecca Bevans

Other students also liked, an easy introduction to statistical significance (with examples), test statistics | definition, interpretation, and examples, what is effect size and why does it matter (examples), what is your plagiarism score.

P-Value in Statistical Hypothesis Tests: What is it?

P value definition.

A p value is used in hypothesis testing to help you support or reject the null hypothesis . The p value is the evidence against a null hypothesis . The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.

P values are expressed as decimals although it may be easier to understand what they are if you convert them to a percentage . For example, a p value of 0.0254 is 2.54%. This means there is a 2.54% chance your results could be random (i.e. happened by chance). That’s pretty tiny. On the other hand, a large p-value of .9(90%) means your results have a 90% probability of being completely random and not due to anything in your experiment. Therefore, the smaller the p-value, the more important (“ significant “) your results.

When you run a hypothesis test , you compare the p value from your test to the alpha level you selected when you ran the test. Alpha levels can also be written as percentages.

P Value vs Alpha level

Alpha levels are controlled by the researcher and are related to confidence levels . You get an alpha level by subtracting your confidence level from 100%. For example, if you want to be 98 percent confident in your research, the alpha level would be 2% (100% – 98%). When you run the hypothesis test, the test will give you a value for p. Compare that value to your chosen alpha level. For example, let’s say you chose an alpha level of 5% (0.05). If the results from the test give you:

• A small p (≤ 0.05), reject the null hypothesis . This is strong evidence that the null hypothesis is invalid.
• A large p (> 0.05) means the alternate hypothesis is weak, so you do not reject the null.

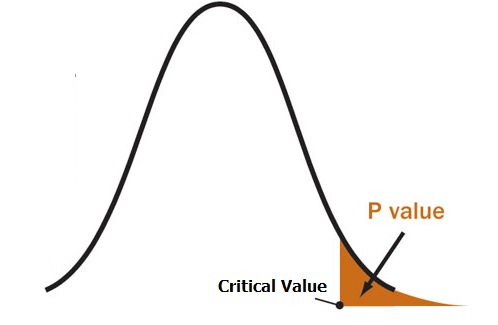
P Values and Critical Values

What if I Don’t Have an Alpha Level?

In an ideal world, you’ll have an alpha level. But if you do not, you can still use the following rough guidelines in deciding whether to support or reject the null hypothesis:

• If p > .10 → “not significant”
• If p ≤ .10 → “marginally significant”
• If p ≤ .05 → “significant”
• If p ≤ .01 → “highly significant.”

How to Calculate a P Value on the TI 83

Example question: The average wait time to see an E.R. doctor is said to be 150 minutes. You think the wait time is actually less. You take a random sample of 30 people and find their average wait is 148 minutes with a standard deviation of 5 minutes. Assume the distribution is normal. Find the p value for this test.

• Press STAT then arrow over to TESTS.
• Press ENTER for Z-Test .
• Arrow over to Stats. Press ENTER.
• Arrow down to μ0 and type 150. This is our null hypothesis mean.
• Arrow down to σ. Type in your std dev: 5.
• Arrow down to xbar. Type in your sample mean : 148.
• Arrow down to n. Type in your sample size : 30.
• Arrow to <μ0 for a left tail test . Press ENTER.
• Arrow down to Calculate. Press ENTER. P is given as .014, or about 1%.

The probability that you would get a sample mean of 148 minutes is tiny, so you should reject the null hypothesis.

Note : If you don’t want to run a test, you could also use the TI 83 NormCDF function to get the area (which is the same thing as the probability value).

Dodge, Y. (2008). The Concise Encyclopedia of Statistics . Springer. Gonick, L. (1993). The Cartoon Guide to Statistics . HarperPerennial.

Warning: The NCBI web site requires JavaScript to function. more...

An official website of the United States government

The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings
• Browse Titles

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].

Hypothesis testing, p values, confidence intervals, and significance.

Jacob Shreffler ; Martin R. Huecker .

Affiliations

Last Update: March 13, 2023 .

• Definition/Introduction

Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting these findings, which may affect the adequate application of the data.

• Issues of Concern

Without a foundational understanding of hypothesis testing, p values, confidence intervals, and the difference between statistical and clinical significance, it may affect healthcare providers' ability to make clinical decisions without relying purely on the research investigators deemed level of significance. Therefore, an overview of these concepts is provided to allow medical professionals to use their expertise to determine if results are reported sufficiently and if the study outcomes are clinically appropriate to be applied in healthcare practice.

Hypothesis Testing

Investigators conducting studies need research questions and hypotheses to guide analyses. Starting with broad research questions (RQs), investigators then identify a gap in current clinical practice or research. Any research problem or statement is grounded in a better understanding of relationships between two or more variables. For this article, we will use the following research question example:

Research Question: Is Drug 23 an effective treatment for Disease A?

Research questions do not directly imply specific guesses or predictions; we must formulate research hypotheses. A hypothesis is a predetermined declaration regarding the research question in which the investigator(s) makes a precise, educated guess about a study outcome. This is sometimes called the alternative hypothesis and ultimately allows the researcher to take a stance based on experience or insight from medical literature. An example of a hypothesis is below.

Research Hypothesis: Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22.

The null hypothesis states that there is no statistical difference between groups based on the stated research hypothesis.

Researchers should be aware of journal recommendations when considering how to report p values, and manuscripts should remain internally consistent.

Regarding p values, as the number of individuals enrolled in a study (the sample size) increases, the likelihood of finding a statistically significant effect increases. With very large sample sizes, the p-value can be very low significant differences in the reduction of symptoms for Disease A between Drug 23 and Drug 22. The null hypothesis is deemed true until a study presents significant data to support rejecting the null hypothesis. Based on the results, the investigators will either reject the null hypothesis (if they found significant differences or associations) or fail to reject the null hypothesis (they could not provide proof that there were significant differences or associations).

To test a hypothesis, researchers obtain data on a representative sample to determine whether to reject or fail to reject a null hypothesis. In most research studies, it is not feasible to obtain data for an entire population. Using a sampling procedure allows for statistical inference, though this involves a certain possibility of error. [1]  When determining whether to reject or fail to reject the null hypothesis, mistakes can be made: Type I and Type II errors. Though it is impossible to ensure that these errors have not occurred, researchers should limit the possibilities of these faults. [2]

Significance

Significance is a term to describe the substantive importance of medical research. Statistical significance is the likelihood of results due to chance. [3]  Healthcare providers should always delineate statistical significance from clinical significance, a common error when reviewing biomedical research. [4]  When conceptualizing findings reported as either significant or not significant, healthcare providers should not simply accept researchers' results or conclusions without considering the clinical significance. Healthcare professionals should consider the clinical importance of findings and understand both p values and confidence intervals so they do not have to rely on the researchers to determine the level of significance. [5]  One criterion often used to determine statistical significance is the utilization of p values.

P values are used in research to determine whether the sample estimate is significantly different from a hypothesized value. The p-value is the probability that the observed effect within the study would have occurred by chance if, in reality, there was no true effect. Conventionally, data yielding a p<0.05 or p<0.01 is considered statistically significant. While some have debated that the 0.05 level should be lowered, it is still universally practiced. [6]  Hypothesis testing allows us to determine the size of the effect.

An example of findings reported with p values are below:

Statement: Drug 23 reduced patients' symptoms compared to Drug 22. Patients who received Drug 23 (n=100) were 2.1 times less likely than patients who received Drug 22 (n = 100) to experience symptoms of Disease A, p<0.05.

Statement:Individuals who were prescribed Drug 23 experienced fewer symptoms (M = 1.3, SD = 0.7) compared to individuals who were prescribed Drug 22 (M = 5.3, SD = 1.9). This finding was statistically significant, p= 0.02.

For either statement, if the threshold had been set at 0.05, the null hypothesis (that there was no relationship) should be rejected, and we should conclude significant differences. Noticeably, as can be seen in the two statements above, some researchers will report findings with < or > and others will provide an exact p-value (0.000001) but never zero [6] . When examining research, readers should understand how p values are reported. The best practice is to report all p values for all variables within a study design, rather than only providing p values for variables with significant findings. [7]  The inclusion of all p values provides evidence for study validity and limits suspicion for selective reporting/data mining.  

While researchers have historically used p values, experts who find p values problematic encourage the use of confidence intervals. [8] . P-values alone do not allow us to understand the size or the extent of the differences or associations. [3]  In March 2016, the American Statistical Association (ASA) released a statement on p values, noting that scientific decision-making and conclusions should not be based on a fixed p-value threshold (e.g., 0.05). They recommend focusing on the significance of results in the context of study design, quality of measurements, and validity of data. Ultimately, the ASA statement noted that in isolation, a p-value does not provide strong evidence. [9]

When conceptualizing clinical work, healthcare professionals should consider p values with a concurrent appraisal study design validity. For example, a p-value from a double-blinded randomized clinical trial (designed to minimize bias) should be weighted higher than one from a retrospective observational study [7] . The p-value debate has smoldered since the 1950s [10] , and replacement with confidence intervals has been suggested since the 1980s. [11]

Confidence Intervals

A confidence interval provides a range of values within given confidence (e.g., 95%), including the accurate value of the statistical constraint within a targeted population. [12]  Most research uses a 95% CI, but investigators can set any level (e.g., 90% CI, 99% CI). [13]  A CI provides a range with the lower bound and upper bound limits of a difference or association that would be plausible for a population. [14]  Therefore, a CI of 95% indicates that if a study were to be carried out 100 times, the range would contain the true value in 95, [15]  confidence intervals provide more evidence regarding the precision of an estimate compared to p-values. [6]

In consideration of the similar research example provided above, one could make the following statement with 95% CI:

Statement: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22; there was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

It is important to note that the width of the CI is affected by the standard error and the sample size; reducing a study sample number will result in less precision of the CI (increase the width). [14]  A larger width indicates a smaller sample size or a larger variability. [16]  A researcher would want to increase the precision of the CI. For example, a 95% CI of 1.43 – 1.47 is much more precise than the one provided in the example above. In research and clinical practice, CIs provide valuable information on whether the interval includes or excludes any clinically significant values. [14]

Null values are sometimes used for differences with CI (zero for differential comparisons and 1 for ratios). However, CIs provide more information than that. [15]  Consider this example: A hospital implements a new protocol that reduced wait time for patients in the emergency department by an average of 25 minutes (95% CI: -2.5 – 41 minutes). Because the range crosses zero, implementing this protocol in different populations could result in longer wait times; however, the range is much higher on the positive side. Thus, while the p-value used to detect statistical significance for this may result in "not significant" findings, individuals should examine this range, consider the study design, and weigh whether or not it is still worth piloting in their workplace.

Similarly to p-values, 95% CIs cannot control for researchers' errors (e.g., study bias or improper data analysis). [14]  In consideration of whether to report p-values or CIs, researchers should examine journal preferences. When in doubt, reporting both may be beneficial. [13]  An example is below:

Reporting both: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22, p = 0.009. There was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

• Clinical Significance

Recall that clinical significance and statistical significance are two different concepts. Healthcare providers should remember that a study with statistically significant differences and large sample size may be of no interest to clinicians, whereas a study with smaller sample size and statistically non-significant results could impact clinical practice. [14]  Additionally, as previously mentioned, a non-significant finding may reflect the study design itself rather than relationships between variables.

Healthcare providers using evidence-based medicine to inform practice should use clinical judgment to determine the practical importance of studies through careful evaluation of the design, sample size, power, likelihood of type I and type II errors, data analysis, and reporting of statistical findings (p values, 95% CI or both). [4]  Interestingly, some experts have called for "statistically significant" or "not significant" to be excluded from work as statistical significance never has and will never be equivalent to clinical significance. [17]

The decision on what is clinically significant can be challenging, depending on the providers' experience and especially the severity of the disease. Providers should use their knowledge and experiences to determine the meaningfulness of study results and make inferences based not only on significant or insignificant results by researchers but through their understanding of study limitations and practical implications.

• Nursing, Allied Health, and Interprofessional Team Interventions

All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts in this chapter. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care. 

• Review Questions
• Access free multiple choice questions on this topic.
• Comment on this article.

Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.

Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

• Cite this Page Shreffler J, Huecker MR. Hypothesis Testing, P Values, Confidence Intervals, and Significance. [Updated 2023 Mar 13]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

• Bulk download StatPearls data from FTP

Related information

• PMC PubMed Central citations
• PubMed Links to PubMed

Similar articles in PubMed

• The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). [PeerJ. 2021] The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). Messam LLM, Weng HY, Rosenberger NWY, Tan ZH, Payet SDM, Santbakshsing M. PeerJ. 2021; 9:e12453. Epub 2021 Nov 24.
• Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. [J Pharm Pract. 2010] Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. Ferrill MJ, Brown DA, Kyle JA. J Pharm Pract. 2010 Aug; 23(4):344-51. Epub 2010 Apr 13.
• Interpreting "statistical hypothesis testing" results in clinical research. [J Ayurveda Integr Med. 2012] Interpreting "statistical hypothesis testing" results in clinical research. Sarmukaddam SB. J Ayurveda Integr Med. 2012 Apr; 3(2):65-9.
• Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. [Dermatol Surg. 2005] Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. Alam M, Barzilai DA, Wrone DA. Dermatol Surg. 2005 Apr; 31(4):462-6.
• Review Is statistical significance testing useful in interpreting data? [Reprod Toxicol. 1993] Review Is statistical significance testing useful in interpreting data? Savitz DA. Reprod Toxicol. 1993; 7(2):95-100.

Recent Activity

• Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearl... Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

9.3 - the p-value approach, example 9-4 section  .

Up until now, we have used the critical region approach in conducting our hypothesis tests. Now, let's take a look at an example in which we use what is called the P -value approach .

Among patients with lung cancer, usually, 90% or more die within three years. As a result of new forms of treatment, it is felt that this rate has been reduced. In a recent study of n = 150 lung cancer patients, y = 128 died within three years. Is there sufficient evidence at the \(\alpha = 0.05\) level, say, to conclude that the death rate due to lung cancer has been reduced?

The sample proportion is:

\(\hat{p}=\dfrac{128}{150}=0.853\)

The null and alternative hypotheses are:

\(H_0 \colon p = 0.90\) and \(H_A \colon p < 0.90\)

The test statistic is, therefore:

\(Z=\dfrac{\hat{p}-p_0}{\sqrt{\dfrac{p_0(1-p_0)}{n}}}=\dfrac{0.853-0.90}{\sqrt{\dfrac{0.90(0.10)}{150}}}=-1.92\)

And, the rejection region is:

Since the test statistic Z = −1.92 < −1.645, we reject the null hypothesis. There is sufficient evidence at the \(\alpha = 0.05\) level to conclude that the rate has been reduced.

Example 9-4 (continued) Section  

What if we set the significance level \(\alpha\) = P (Type I Error) to 0.01? Is there still sufficient evidence to conclude that the death rate due to lung cancer has been reduced?

In this case, with \(\alpha = 0.01\), the rejection region is Z ≤ −2.33. That is, we reject if the test statistic falls in the rejection region defined by Z ≤ −2.33:

Because the test statistic Z = −1.92 > −2.33, we do not reject the null hypothesis. There is insufficient evidence at the \(\alpha = 0.01\) level to conclude that the rate has been reduced.

In the first part of this example, we rejected the null hypothesis when \(\alpha = 0.05\). And, in the second part of this example, we failed to reject the null hypothesis when \(\alpha = 0.01\). There must be some level of \(\alpha\), then, in which we cross the threshold from rejecting to not rejecting the null hypothesis. What is the smallest \(\alpha \text{ -level}\) that would still cause us to reject the null hypothesis?

We would, of course, reject any time the critical value was smaller than our test statistic −1.92:

That is, we would reject if the critical value were −1.645, −1.83, and −1.92. But, we wouldn't reject if the critical value were −1.93. The \(\alpha \text{ -level}\) associated with the test statistic −1.92 is called the P -value . It is the smallest \(\alpha \text{ -level}\) that would lead to rejection. In this case, the P -value is:

P ( Z < −1.92) = 0.0274

So far, all of the examples we've considered have involved a one-tailed hypothesis test in which the alternative hypothesis involved either a less than (<) or a greater than (>) sign. What happens if we weren't sure of the direction in which the proportion could deviate from the hypothesized null value? That is, what if the alternative hypothesis involved a not-equal sign (≠)? Let's take a look at an example.

What if we wanted to perform a " two-tailed " test? That is, what if we wanted to test:

\(H_0 \colon p = 0.90\) versus \(H_A \colon p \ne 0.90\)

at the \(\alpha = 0.05\) level?

Let's first consider the critical value approach . If we allow for the possibility that the sample proportion could either prove to be too large or too small, then we need to specify a threshold value, that is, a critical value, in each tail of the distribution. In this case, we divide the " significance level " \(\alpha\) by 2 to get \(\alpha/2\):

That is, our rejection rule is that we should reject the null hypothesis \(H_0 \text{ if } Z ≥ 1.96\) or we should reject the null hypothesis \(H_0 \text{ if } Z ≤ −1.96\). Alternatively, we can write that we should reject the null hypothesis \(H_0 \text{ if } |Z| ≥ 1.96\). Because our test statistic is −1.92, we just barely fail to reject the null hypothesis, because 1.92 < 1.96. In this case, we would say that there is insufficient evidence at the \(\alpha = 0.05\) level to conclude that the sample proportion differs significantly from 0.90.

Now for the P -value approach . Again, needing to allow for the possibility that the sample proportion is either too large or too small, we multiply the P -value we obtain for the one-tailed test by 2:

That is, the P -value is:

\(P=P(|Z|\geq 1.92)=P(Z>1.92 \text{ or } Z<-1.92)=2 \times 0.0274=0.055\)

Because the P -value 0.055 is (just barely) greater than the significance level \(\alpha = 0.05\), we barely fail to reject the null hypothesis. Again, we would say that there is insufficient evidence at the \(\alpha = 0.05\) level to conclude that the sample proportion differs significantly from 0.90.

Let's close this example by formalizing the definition of a P -value, as well as summarizing the P -value approach to conducting a hypothesis test.

The P -value is the smallest significance level \(\alpha\) that leads us to reject the null hypothesis.

Alternatively (and the way I prefer to think of P -values), the P -value is the probability that we'd observe a more extreme statistic than we did if the null hypothesis were true.

If the P -value is small, that is, if \(P ≤ \alpha\), then we reject the null hypothesis \(H_0\).

Note! Section  

By the way, to test \(H_0 \colon p = p_0\), some statisticians will use the test statistic:

\(Z=\dfrac{\hat{p}-p_0}{\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}}\)

rather than the one we've been using:

\(Z=\dfrac{\hat{p}-p_0}{\sqrt{\dfrac{p_0(1-p_0)}{n}}}\)

One advantage of doing so is that the interpretation of the confidence interval — does it contain \(p_0\)? — is always consistent with the hypothesis test decision, as illustrated here:

For the sake of ease, let:

\(se(\hat{p})=\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}\)

Two-tailed test. In this case, the critical region approach tells us to reject the null hypothesis \(H_0 \colon p = p_0\) against the alternative hypothesis \(H_A \colon p \ne p_0\):

if \(Z=\dfrac{\hat{p}-p_0}{se(\hat{p})} \geq z_{\alpha/2}\) or if \(Z=\dfrac{\hat{p}-p_0}{se(\hat{p})} \leq -z_{\alpha/2}\)

which is equivalent to rejecting the null hypothesis:

if \(\hat{p}-p_0 \geq z_{\alpha/2}se(\hat{p})\) or if \(\hat{p}-p_0 \leq -z_{\alpha/2}se(\hat{p})\)

if \(p_0 \geq \hat{p}+z_{\alpha/2}se(\hat{p})\) or if \(p_0 \leq \hat{p}-z_{\alpha/2}se(\hat{p})\)

That's the same as saying that we should reject the null hypothesis \(H_0 \text{ if } p_0\) is not in the \(\left(1-\alpha\right)100\%\) confidence interval!

Left-tailed test. In this case, the critical region approach tells us to reject the null hypothesis \(H_0 \colon p = p_0\) against the alternative hypothesis \(H_A \colon p < p_0\):

if \(Z=\dfrac{\hat{p}-p_0}{se(\hat{p})} \leq -z_{\alpha}\)

if \(\hat{p}-p_0 \leq -z_{\alpha}se(\hat{p})\)

if \(p_0 \geq \hat{p}+z_{\alpha}se(\hat{p})\)

That's the same as saying that we should reject the null hypothesis \(H_0 \text{ if } p_0\) is not in the upper \(\left(1-\alpha\right)100\%\) confidence interval:

\((0,\hat{p}+z_{\alpha}se(\hat{p}))\)

What is The Null Hypothesis & When Do You Reject The Null Hypothesis

Julia Simkus

Editor at Simply Psychology

BA (Hons) Psychology, Princeton University

Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.

Learn about our Editorial Process

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

A null hypothesis is a statistical concept suggesting no significant difference or relationship between measured variables. It’s the default assumption unless empirical evidence proves otherwise.

The null hypothesis states no relationship exists between the two variables being studied (i.e., one variable does not affect the other).

The null hypothesis is the statement that a researcher or an investigator wants to disprove.

Testing the null hypothesis can tell you whether your results are due to the effects of manipulating ​ the dependent variable or due to random chance. 

How to Write a Null Hypothesis

Null hypotheses (H0) start as research questions that the investigator rephrases as statements indicating no effect or relationship between the independent and dependent variables.

It is a default position that your research aims to challenge or confirm.

For example, if studying the impact of exercise on weight loss, your null hypothesis might be:

There is no significant difference in weight loss between individuals who exercise daily and those who do not.

Examples of Null Hypotheses

When Do We Reject The Null Hypothesis? 

We reject the null hypothesis when the data provide strong enough evidence to conclude that it is likely incorrect. This often occurs when the p-value (probability of observing the data given the null hypothesis is true) is below a predetermined significance level.

If the collected data does not meet the expectation of the null hypothesis, a researcher can conclude that the data lacks sufficient evidence to back up the null hypothesis, and thus the null hypothesis is rejected. 

Rejecting the null hypothesis means that a relationship does exist between a set of variables and the effect is statistically significant ( p > 0.05).

If the data collected from the random sample is not statistically significance , then the null hypothesis will be accepted, and the researchers can conclude that there is no relationship between the variables. 

You need to perform a statistical test on your data in order to evaluate how consistent it is with the null hypothesis. A p-value is one statistical measurement used to validate a hypothesis against observed data.

Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis.

The level of statistical significance is often expressed as a  p  -value between 0 and 1. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.

Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01) as general guidelines to decide if you should reject or keep the null.

When your p-value is less than or equal to your significance level, you reject the null hypothesis.

In other words, smaller p-values are taken as stronger evidence against the null hypothesis. Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis.

In this case, the sample data provides insufficient data to conclude that the effect exists in the population.

Because you can never know with complete certainty whether there is an effect in the population, your inferences about a population will sometimes be incorrect.

When you incorrectly reject the null hypothesis, it’s called a type I error. When you incorrectly fail to reject it, it’s called a type II error.

Why Do We Never Accept The Null Hypothesis?

The reason we do not say “accept the null” is because we are always assuming the null hypothesis is true and then conducting a study to see if there is evidence against it. And, even if we don’t find evidence against it, a null hypothesis is not accepted.

A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist. 

It is risky to conclude that the null hypothesis is true merely because we did not find evidence to reject it. It is always possible that researchers elsewhere have disproved the null hypothesis, so we cannot accept it as true, but instead, we state that we failed to reject the null. 

One can either reject the null hypothesis, or fail to reject it, but can never accept it.

Why Do We Use The Null Hypothesis?

We can never prove with 100% certainty that a hypothesis is true; We can only collect evidence that supports a theory. However, testing a hypothesis can set the stage for rejecting or accepting this hypothesis within a certain confidence level.

The null hypothesis is useful because it can tell us whether the results of our study are due to random chance or the manipulation of a variable (with a certain level of confidence).

A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis.

Rejecting the null hypothesis sets the stage for further experimentation to see if a relationship between two variables exists. 

Hypothesis testing is a critical part of the scientific method as it helps decide whether the results of a research study support a particular theory about a given population. Hypothesis testing is a systematic way of backing up researchers’ predictions with statistical analysis.

It helps provide sufficient statistical evidence that either favors or rejects a certain hypothesis about the population parameter. 

Purpose of a Null Hypothesis 

• The primary purpose of the null hypothesis is to disprove an assumption. 
• Whether rejected or accepted, the null hypothesis can help further progress a theory in many scientific cases.
• A null hypothesis can be used to ascertain how consistent the outcomes of multiple studies are.

Do you always need both a Null Hypothesis and an Alternative Hypothesis?

The null (H0) and alternative (Ha or H1) hypotheses are two competing claims that describe the effect of the independent variable on the dependent variable. They are mutually exclusive, which means that only one of the two hypotheses can be true. 

While the null hypothesis states that there is no effect in the population, an alternative hypothesis states that there is statistical significance between two variables. 

The goal of hypothesis testing is to make inferences about a population based on a sample. In order to undertake hypothesis testing, you must express your research hypothesis as a null and alternative hypothesis. Both hypotheses are required to cover every possible outcome of the study. 

What is the difference between a null hypothesis and an alternative hypothesis?

The alternative hypothesis is the complement to the null hypothesis. The null hypothesis states that there is no effect or no relationship between variables, while the alternative hypothesis claims that there is an effect or relationship in the population.

It is the claim that you expect or hope will be true. The null hypothesis and the alternative hypothesis are always mutually exclusive, meaning that only one can be true at a time.

What are some problems with the null hypothesis?

One major problem with the null hypothesis is that researchers typically will assume that accepting the null is a failure of the experiment. However, accepting or rejecting any hypothesis is a positive result. Even if the null is not refuted, the researchers will still learn something new.

Why can a null hypothesis not be accepted?

We can either reject or fail to reject a null hypothesis, but never accept it. If your test fails to detect an effect, this is not proof that the effect doesn’t exist. It just means that your sample did not have enough evidence to conclude that it exists.

We can’t accept a null hypothesis because a lack of evidence does not prove something that does not exist. Instead, we fail to reject it.

Failing to reject the null indicates that the sample did not provide sufficient enough evidence to conclude that an effect exists.

If the p-value is greater than the significance level, then you fail to reject the null hypothesis.

Is a null hypothesis directional or non-directional?

A hypothesis test can either contain an alternative directional hypothesis or a non-directional alternative hypothesis. A directional hypothesis is one that contains the less than (“<“) or greater than (“>”) sign.

A nondirectional hypothesis contains the not equal sign (“≠”).  However, a null hypothesis is neither directional nor non-directional.

A null hypothesis is a prediction that there will be no change, relationship, or difference between two variables.

The directional hypothesis or nondirectional hypothesis would then be considered alternative hypotheses to the null hypothesis.

Gill, J. (1999). The insignificance of null hypothesis significance testing.  Political research quarterly ,  52 (3), 647-674.

Krueger, J. (2001). Null hypothesis significance testing: On the survival of a flawed method.  American Psychologist ,  56 (1), 16.

Masson, M. E. (2011). A tutorial on a practical Bayesian alternative to null-hypothesis significance testing.  Behavior research methods ,  43 , 679-690.

Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy.  Psychological methods ,  5 (2), 241.

Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test.  Psychological bulletin ,  57 (5), 416.

The p value – definition and interpretation of p-values in statistics

This article examines the most common statistic reported in scientific papers and used in applied statistical analyses – the p -value . The article goes through the definition illustrated with examples, discusses its utility, interpretation, and common misinterpretations of observed statistical significance and significance levels. It is structured as follows:

What does ‘ p ‘ in ‘ p -value’ stand for?

What does p measure and how to interpret it.

• A p-value only makes sense under a specified null hypothesis

How to calculate a p -value?

A practical example, p -values as convenient summary statistics.

• Quantifying the relative uncertainty of data

Easy comparison of different statistical tests

• p -value interpretation in outcomes of experiments (randomized controlled trials)
• p -value interpretation in regressions and correlations of observational data

Mistaking statistical significance with practical significance

Treating the significance level as likelihood for the observed effect, treating p -values as likelihoods attached to hypotheses, a high p -value means the null hypothesis is true, lack of statistical significance suggests a small effect size, p -value definition and meaning.

The technical definition of the p -value is (based on [4,5,6]):

A p -value is the probability of the data-generating mechanism corresponding to a specified null hypothesis to produce an outcome as extreme or more extreme than the one observed.

However, it is only straightforward to understand for those already familiar in detail with terms such as ‘probability’, ‘null hypothesis’, ‘data generating mechanism’, ‘extreme outcome’. These, in turn, require knowledge of what a ‘hypothesis’, a ‘statistical model’ and ‘statistic’ mean, and so on. While some of these will be explained on a cursory level in the following paragraphs, those looking for deeper understanding should consider consulting the following glossary definitions: statistical model , hypothesis , null hypothesis , statistic .

A slightly less technical and therefore more accessible definition is:

A p -value quantifies how likely it is to erroneously reject a specific statistical hypothesis, were it true, based on a given set of data.

Let us break these down and examine several examples to make both of these definitions make sense.

p stands for p robability where probability means the frequency with which an event occurs under certain assumptions. The most common example is the frequency with which a coin lands heads under the assumption that it is equally balanced (a fair coin toss ). That frequency is 0.5 (50%).

Capital ‘P’ stands for probability in general, whereas lowercase ‘ p ‘ refers to the probability of a particular data realization. To expand on the coin toss example: P would stand for the probability of heads in general, whereas p could refer to the probability of landing a series of five heads in a row, or the probability of landing less than or equal to 38 heads out of 100 coin flips.

Given that it was established that p stands for probability, it is easy to figure out it measures a sort of probability.

In everyday language the term ‘probability’ might be used as synonymous to ‘chance’, ‘likelihood’, ‘odds’, e.g. there is 90% probability that it will rain tomorrow. However, in statistics one cannot speak of ‘probability’ without specifying a mechanism which generates the observed data. A simple example of such a mechanism is a device which produces fair coin tosses. A statistical model based on this data-generating mechanism can be put forth and under that model the probability of 38 or less heads out of 100 tosses can be estimated to be 1.05%, for example by using a binomial calculator . The p -value against the model of a fair coin would be ~0.01 (rounding it to 0.01 from hereon for the purposes of the article).

The way to interpret that p -value is: observing 38 heads or less out of the 100 tosses could have happened in only 1% of infinitely many series of 100 fair coin tosses. The null hypothesis in this case is defined as the coin being fair, therefore having a 50% chance for heads and 50% chance for tails on each toss.

Assuming the null hypothesis is true allows the comparison of the observed data to what would have been expected under the null. It turns out the particular observation of 38/100 heads is a rather improbable and thus surprising outcome under the assumption of the null hypothesis. This is measured by the low p -value which also accounts for more extreme outcomes such as 37/100, 36/100, and so on all the way to 0/100.

If one had a predefined level of statistical significance at 0.05 then one would claim that the outcome is statistically significant since it’s p -value of 0.01 meets the 0.05 significance level (0.01 ≤ 0.05). A visual representation of the relationship between p -values, significance level ( p -value threshold), and statistical significance of an outcome is illustrated visually in this graph:

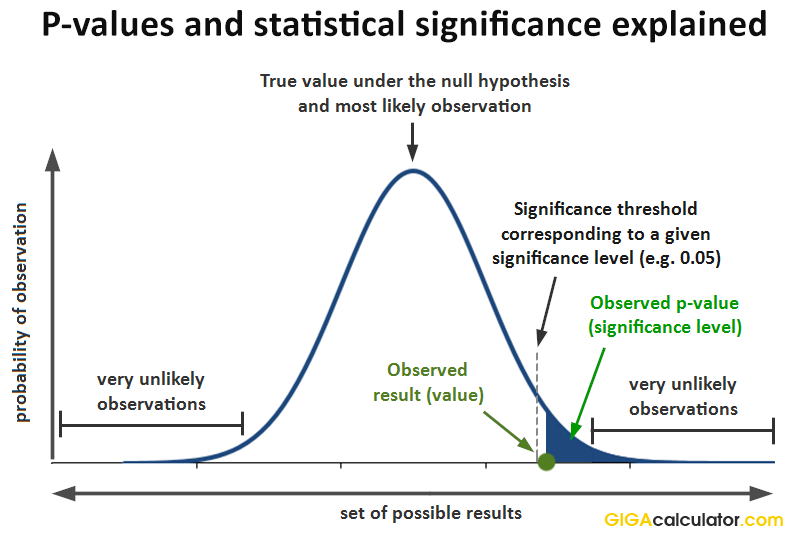
In fact, had the significance threshold been at any value above 0.01, the outcome would have been statistically significant, therefore it is usually said that with a p -value of 0.01, the outcome is statistically significant at any level above 0.01 .

Continuing with the interpretation: were one to reject the null hypothesis based on this p -value of 0.01, they would be acting as if a significance level of 0.01 or lower provides sufficient evidence against the hypothesis of the coin being fair. One could interpret this as a rule for a long-run series of experiments and inferences . In such a series, by using this p -value threshold one would incorrectly reject the fair coin hypothesis in at most 1 out of 100 cases, regardless of whether the coin is actually fair in any one of them. An incorrect rejection of the null is often called a type I error as opposed to a type II error which is to incorrectly fail to reject a null.

A more intuitive interpretation proceeds without reference to hypothetical long-runs. This second interpretation comes in the form of a strong argument from coincidence :

• there was a low probability (0.01 or 1%) that something would have happened assuming the null was true
• it did happen so it has to be an unusual (to the extent that the p -value is low) coincidence that it happened
• this warrants the conclusion to reject the null hypothesis

( source ). It stems from the concept of severe testing as developed by Prof. Deborah Mayo in her various works [1,2,3,4,5] and reflects an error-probabilistic approach to inference.

A p -value only makes sense under a specified null hypothesis

It is important to understand why a specified ‘null hypothesis’ should always accompany any reported p -value and why p-values are crucial in so-called Null Hypothesis Statistical Tests (NHST) . Statistical significance only makes sense when referring to a particular statistical model which in turn corresponds to a given null hypothesis. A p -value calculation has a statistical model and a statistical null hypothesis defined within it as prerequisites, and a statistical null is only interesting because of some tightly related substantive null such as ‘this treatment improves outcomes’. The relationship is shown in the chart below:

In the coin example, the substantive null that is interesting to (potentially) reject is the claim that the coin is fair. It translates to a statistical null hypothesis (model) with the following key properties:

• heads having 50% chance and tails having 50% chance, on each toss
• independence of each toss from any other toss. The outcome of any given coin toss does not depend on past or future coin tosses.
• homogeneity of the coin behavior over time (the true chance does not change across infinitely many tosses)
• a binomial error distribution

The resulting p -value of 0.01 from the coin toss experiment should be interpreted as the probability only under these particular assumptions.

What happens, however, if someone is interested in rejecting the claim that the coin is somewhat biased against heads? To be precise: the claim that it has a true frequency of heads of 40% or less (hence 60% for tails) is the one they are looking to deny with a certain evidential threshold.

The p -value needs to be recalculated under their null hypothesis so now the same 38 heads out of 100 tosses result in a p -value of ~0.38 ( calculation ). If they were interested in rejecting such a null hypothesis, then this data provide poor evidence against it since a 38/100 outcome would not be unusual at all if it were in fact true (p ≤ 0.38 would occur with probability 38%).

Similarly, the p -value needs to be recalculated for a claim of bias in the other direction, say that the coin produces heads with a frequency of 60% or more. The probability of observing 38 or fewer out of 100 under this null hypothesis is so extremely small ( p -value ~= 0.000007364 or 7.364 x 10 -6 in standard form , calculation ) that maintaining a claim for 60/40 bias in favor of heads becomes near-impossible for most practical purposes.

A p -value can be calculated for any frequentist statistical test. Common types of statistical tests include tests for:

• absolute difference in proportions;
• absolute difference in means;
• relative difference in means or proportions;
• goodness-of-fit;
• homogeneity
• independence
• analysis of variance (ANOVA)

and others. Different statistics would be computed depending on the error distribution of the parameter of interest in each case, e.g. a t value, z value, chi-square (Χ 2 ) value, f -value, and so on.

p -values can then be calculated based on the cumulative distribution functions (CDFs) of these statistics whereas pre-test significance thresholds (critical values) can be computed based on the inverses of these functions. You can try these by plugging different inputs in our critical value calculator , and also by consulting its documentation.

In its generic form, a p -value formula can be written down as:

p = P(d(X) ≥ d(x 0 ); H 0 )

where P stands for probability, d(X) is a test statistic (distance function) of a random variable X , x 0 is a typical realization of X and H 0 is the selected null hypothesis. The semi-colon means ‘assuming’. The distance function is the aforementioned cumulative distribution function for the relevant error distribution. In its generic form a distance function equation can be written as:

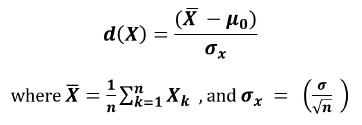
X -bar is the arithmetic mean of the observed values, μ 0 is a hypothetical or expected mean to which X is compared, and n is the sample size. The result of a distance function will often be expressed in a standardized form – the number of standard deviations between the observed value and the expected value.

The p -value calculation is different in each case and so a different formula will be applied depending on circumstances. You can see examples in the p -values reported in our statistical calculators, such as the statistical significance calculator for difference of means or proportions , the Chi-square calculator , the risk ratio calculator , odds ratio calculator , hazard ratio calculator , and the normality calculator .

A very fresh (as of late 2020) example of the application of p -values in scientific hypothesis testing can be found in the recently concluded COVID-19 clinical trials. Multiple vaccines for the virus which spread from China in late 2019 and early 2020 have been tested on tens of thousands of volunteers split randomly into two groups – one gets the vaccine and the other gets a placebo. This is called a randomized controlled trial (RCT). The main parameter of interest is the difference between the rates of infections in the two groups. An appropriate test is the t-test for difference of proportions, but the same data can be examined in terms of risk ratios or odds ratio.

The null hypothesis in many of these medical trials is that the vaccine is at least 30% efficient. A statistical model can be built about the expected difference in proportions if the vaccine’s efficiency is 30% or less, and then the actual observed data from a medical trial can be compared to that null hypothesis. Most trials set their significance level at the minimum required by the regulatory bodies (FDA, EMA, etc.), which is usually set at 0.05 . So, if the p -value from a vaccine trial is calculated to be below 0.05, the outcome would be statistically significant and the null hypothesis of the vaccine being less than or equal to 30% efficient would be rejected.

Let us say a vaccine trial results in a p -value of 0.0001 against that null hypothesis. As this is highly unlikely under the assumption of the null hypothesis being true, it provides very strong evidence against the hypothesis that the tested treatment has less than 30% efficiency.

However, many regulators stated that they require at least 50% proven efficiency. They posit a different null hypothesis and so the p -value presented before these bodies needs to be calculated against it. This p -value would be somewhat increased since 50% is a higher null value than 30%, but given that the observed effects of the first vaccines to finalize their trials are around 95% with 95% confidence interval bounds hovering around 90%, the p -value against a null hypothesis stating that the vaccine’s efficiency is 50% or less is likely to still be highly statistically significant, say at 0.001 . Such an outcome is to be interpreted as follows: had the efficiency been 50% or below, such an extreme outcome would have most likely not been observed, therefore one can proceed to reject the claim that the vaccine has efficiency of 50% or less with a significance level of 0.001 .

While this example is fictitious in that it doesn’t reference any particular experiment, it should serve as a good illustration of how null hypothesis statistical testing (NHST) operates based on p -values and significance thresholds.

The utility of p -values and statistical significance

It is not often appreciated how much utility p-values bring to the practice of performing statistical tests for scientific and business purposes.

Quantifying relative uncertainty of data

First and foremost, p -values are a convenient expression of the uncertainty in the data with respect to a given claim. They quantify how unexpected a given observation is, assuming some claim which is put to the test is true. If the p-value is low the probability that it would have been observed under the null hypothesis is low. This means the uncertainty the data introduce is high. Therefore, anyone defending the substantive claim which corresponds to the statistical null hypothesis would be pressed to concede that their position is untenable in the face of such data.

If the p-value is high, then the uncertainty with regard to the null hypothesis is low and we are not in a position to reject it, hence the corresponding claim can still be maintained.

As evident by the generic p -value formula and the equation for a distance function which is a part of it, a p -value incorporates information about:

• the observed effect size relative to the null effect size
• the sample size of the test
• the variance and error distribution of the statistic of interest

It would be much more complicated to communicate the outcomes of a statistical test if one had to communicate all three pieces of information. Instead, by way of a single value on the scale of 0 to 1 one can communicate how surprising an outcome is. This value is affected by any change in any of these variables.

This quality stems from the fact that assuming that a p -value from one statistical test can easily and directly be compared to another. The minimal assumptions behind significance tests mean that given that all of them are met, the strength of the statistical evidence offered by data relative to a null hypothesis of interest is the same in two tests if they have approximately equal p -values.

This is especially useful in conducting meta-analyses of various sorts, or for combining evidence from multiple tests.

p -value interpretation in outcomes of experiments

When a p -value is calculated for the outcome of a randomized controlled experiment, it is used to assess the strength of evidence against a null hypothesis of interest, such as that a given intervention does not have a positive effect. If H 0 : μ 0 ≤ 0% and the observed effect is μ 1 = 30% and the calculated p -value is 0.025, this can be used to reject the claim H 0 : μ 0 ≤ 0% at any significance level ≥ 0.025. This, in turn, allows us to claim that H 1 , a complementary hypothesis called the ‘alternative hypothesis’, is in fact true. In this case since H 0 : μ 0 ≤ 0% then H 1 : μ 1 > 0% in order to exhaust the parameter space, as illustrated below:

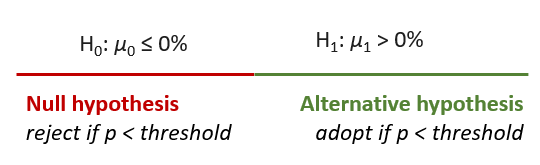
A claim as the above corresponds to what is called a one-sided null hypothesis . There could be a point null as well, for example the claim that an intervention has no effect whatsoever translates to H 0 : μ 0 = 0%. In such a case the corresponding p -value refers to that point null and hence should be interpreted as rejecting the claim of the effect being exactly zero. For those interested in the differences between point null hypotheses and one-sided hypotheses the articles on onesided.org should be an interesting read. TLDR: most of the time you’d want to reject a directional claim and hence a one-tailed p -value should be reported [8] .

These finer points aside, after observing a low enough p -value, one can claim the rejection of the null and hence the adoption of the complementary alternative hypothesis as true. The alternative hypothesis is simply a negation of the null and is therefore a composite claim such as ‘there is a positive effect’ or ‘there is some non-zero effect’. Note that any inference about a particular effect size within the alternative space has not been tested and hence claiming it has probability equal to p calculated against a zero effect null hypothesis (a.k.a. the nil hypothesis) does not make sense.

p – value interpretation in regressions and correlations of observational data

When performing statistical analyses of observational data p -values are often calculated for regressors in addition to regression coefficients and for the correlation in addition to correlation coefficients. A p -value falling below a specific statistical significance threshold measures how surprising the observed correlation or regression coefficient would be if the variable of interest is in fact orthogonal to the outcome variable. That is – how likely would it be to observe the apparent relationship, if there was no actual relationship between the variable and the outcome variable.

Our correlation calculator outputs both p -values and confidence intervals for the calculated coefficients and is an easy way to explore the concept in the case of correlations. Extrapolating to regressions is then straightforward.

Misinterpretations of statistically significant p -values

There are several common misinterpretations [7] of p -values and statistical significance and no calculator can save one from falling for them. The following errors are often committed when a result is seen as statistically significant.

A result may be highly statistically significant (e.g. p -value 0.0001) but it might still have no practical consequences due to a trivial effect size. This often happens with overpowered designs, but it can also happen in a properly designed statistical test. This error can be avoided by always reporting the effect size and confidence intervals around it.

Observing a highly significant result, say p -value 0.01 does not mean that the likelihood that the observed difference is the true difference. In fact, that likelihood is much, much smaller. Remember that statistical significance has a strict meaning in the NHST framework.

For example, if the observed effect size μ 1 from an intervention is 20% improvement in some outcome and a p -value against the null hypothesis of μ 0 ≤ 0% has been calculated to be 0.01, it does not mean that one can reject μ 0 ≤ 20% with a p -value of 0.01. In fact, the p -value against μ 0 ≤ 20% would be 0.5, which is not statistically significant by any measure.

To make claims about a particular effect size it is recommended to use confidence intervals or severity, or both.

For example, stating that a p -value of 0.02 means that there is 98% probability that the alternative hypothesis is true or that there is 2% probability that the null hypothesis is true . This is a logical error.

By design, even if the null hypothesis is true, p -values equal to or lower than 0.02 would be observed exactly 2% of the time, so one cannot use the fact that a low p -value has been observed to argue there is only 2% probability that the null hypothesis is true. Frequentist and error-statistical methods do not allow one to attach probabilities to hypotheses or claims, only to events [4] . Doing so requires an exhaustive list of hypotheses and prior probabilities attached to them which goes firmly into decision-making territory. Put in Bayesian terms, the p -value is not a posterior probability.

Misinterpretations of statistically non-significant outcomes

Statistically non-significant p-values – that is, p is greater than the specified significance threshold α (alpha), can lead to a different set of misinterpretations. Due to the ubiquitous use of p -values, these are committed often as well.

Treating a high p -value / low significance level as evidence, by itself, that the null hypothesis is true is a common mistake. For example, after observing p = 0.2 one may claim this is evidence that there is no effect, e.g. no difference between two means, is a common mistake.

However, it is trivial to demonstrate why it is wrong to interpret a high p -value as providing support for the null hypothesis. Take a simple experiment in which one measures only 2 (two) people or objects in the control and treatment groups. The p -value for this test of significance will surely not be statistically significant. Does that mean that the intervention is ineffective? Of course not, since that claim has not been tested severely enough. Using a statistic such as severity can completely eliminate this error [4,5] .

A more detailed response would say that failure to observe a statistically significant result, given that the test has enough statistical power, can be used to argue for accepting the null hypothesis to the extent warranted by the power and with reference to the minimum detectable effect for which it was calculated. For example, if the statistical test had 99% power to detect an effect of size μ 1 at level α and it failed, then it could be argued that it is quite unlikely that there exists and effect of size μ 1 or greater as in that case one would have most likely observed a significant p -value.

This is a softer version of the above mistake wherein instead of claiming support for the null hypothesis, a low p -value is taken, by itself, as indicating that the effect size must be small.

This is a mistake since the test might have simply lacked power to exclude many effects of meaningful size. Examining confidence intervals and performing severity calculations against particular hypothesized effect sizes would be a way to avoid this issue.

References:

[1] Mayo, D.G. 1983. “An Objective Theory of Statistical Testing.” Synthese 57 (3): 297–340. DOI:10.1007/BF01064701. [2] Mayo, D.G. 1996 “Error and the Growth of Experimental Knowledge.” Chicago, Illinois: University of Chicago Press. DOI:10.1080/106351599260247. [3] Mayo, D.G., and A. Spanos. 2006. “Severe Testing as a Basic Concept in a Neyman–Pearson Philosophy of Induction.” The British Journal for the Philosophy of Science 57 (2): 323–357. DOI:10.1093/bjps/axl003. [4] Mayo, D.G., and A. Spanos. 2011. “Error Statistics.” Vol. 7, in Handbook of Philosophy of Science Volume 7 – Philosophy of Statistics , by D.G., Spanos, A. et al. Mayo, 1-46. Elsevier. [5] Mayo, D.G. 2018 “Statistical Inference as Severe Testing.” Cambridge: Cambridge University Press. ISBN: 978-1107664647 [6] Georgiev, G.Z. (2019) “Statistical Methods in Online A/B Testing”, ISBN: 978-1694079725 [7] Greenland, S. et al. (2016) “Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations”, European Journal of Epidemiology 31:337–350; DOI:10.1007/s10654-016-0149-3 [8] Georgiev, G.Z. (2018) “Directional claims require directional (statistical) hypotheses” [online, accessed on Dec 07, 2020, at https://www.onesided.org/articles/directional-claims-require-directional-hypotheses.php]

An applied statistician, data analyst, and optimizer by calling, Georgi has expertise in web analytics, statistics, design of experiments, and business risk management. He covers a variety of topics where mathematical models and statistics are useful. Georgi is also the author of “Statistical Methods in Online A/B Testing”.

Recent Articles

• Mastering Formulas in Baking: Baker’s Math, Kitchen Conversions, + More
• Margin vs. Markup: Decoding Profitability in Simple Terms
• How Much Do I Have to Earn Per Hour to Afford the Cost of Living?
• How to Calculate for VAT When Traveling Abroad
• Mathematics in the Kitchen
• Search GIGA Articles
• Cybersecurity
• Home & Garden
• Mathematics

• Quality Improvement
• Talk To Minitab

How to Correctly Interpret P Values

Topics: Hypothesis Testing

The P value is used all over statistics, from t-tests to regression analysis . Everyone knows that you use P values to determine statistical significance in a hypothesis test . In fact, P values often determine what studies get published and what projects get funding.

Despite being so important, the P value is a slippery concept that people often interpret incorrectly. How do you interpret P values?

In this post, I'll help you to understand P values in a more intuitive way and to avoid a very common misinterpretation that can cost you money and credibility.

What Is the Null Hypothesis in Hypothesis Testing?

In every experiment, there is an effect or difference between groups that the researchers are testing. It could be the effectiveness of a new drug, building material, or other intervention that has benefits. Unfortunately for the researchers, there is always the possibility that there is no effect, that is, that there is no difference between the groups. This lack of a difference is called the null hypothesis , which is essentially the position a devil’s advocate would take when evaluating the results of an experiment.

To see why, let’s imagine an experiment for a drug that we know is totally ineffective. The null hypothesis is true: there is no difference between the experimental groups at the population level.

Despite the null being true, it’s entirely possible that there will be an effect in the sample data due to random sampling error. In fact, it is extremely unlikely that the sample groups will ever exactly equal the null hypothesis value. Consequently, the devil’s advocate position is that the observed difference in the sample does not reflect a true difference between populations .

What Are P Values?

• High P values: your data are likely with a true null.
• Low P values: your data are unlikely with a true null.

A low P value suggests that your sample provides enough evidence that you can reject the null hypothesis for the entire population.

How Do You Interpret P Values?

For example, suppose that a vaccine study produced a P value of 0.04. This P value indicates that if the vaccine had no effect, you’d obtain the observed difference or more in 4% of studies due to random sampling error.

P values address only one question: how likely are your data, assuming a true null hypothesis? It does not measure support for the alternative hypothesis. This limitation leads us into the next section to cover a very common misinterpretation of P values.

hbspt.cta._relativeUrls=true;hbspt.cta.load(3447555, '16128196-352b-4dd2-8356-f063c37c5b2a', {"useNewLoader":"true","region":"na1"});

P values are not the probability of making a mistake.

Incorrect interpretations of P values are very common. The most common mistake is to interpret a P value as the probability of making a mistake by rejecting a true null hypothesis (a Type I error ).

There are several reasons why P values can’t be the error rate.

First, P values are calculated based on the assumptions that the null is true for the population and that the difference in the sample is caused entirely by random chance. Consequently, P values can’t tell you the probability that the null is true or false because it is 100% true from the perspective of the calculations.

Second, while a low P value indicates that your data are unlikely assuming a true null, it can’t evaluate which of two competing cases is more likely:

• The null is true but your sample was unusual.
• The null is false.

Determining which case is more likely requires subject area knowledge and replicate studies.

Let’s go back to the vaccine study and compare the correct and incorrect way to interpret the P value of 0.04:

• Correct: Assuming that the vaccine had no effect, you’d obtain the observed difference or more in 4% of studies due to random sampling error.  
• Incorrect: If you reject the null hypothesis, there’s a 4% chance that you’re making a mistake.

To see a graphical representation of how hypothesis tests work, see my post: Understanding Hypothesis Tests: Significance Levels and P Values .

What Is the True Error Rate?

If a P value is not the error rate, what the heck is the error rate? (Can you guess which way this is heading now?)

Sellke et al.* have estimated the error rates associated with different P values. While the precise error rate depends on various assumptions (which I discuss here ), the table summarizes them for middle-of-the-road assumptions.

Do the higher error rates in this table surprise you? Unfortunately, the common misinterpretation of P values as the error rate creates the illusion of substantially more evidence against the null hypothesis than is justified. As you can see, if you base a decision on a single study with a P value near 0.05, the difference observed in the sample may not exist at the population level. That can be costly!

Now that you know how to interpret P values, read my five guidelines for how to use P values and avoid mistakes .

You can also read my rebuttal to an academic journal that actually banned P values !

An exciting study about the reproducibility of experimental results was published in August 2015. This study highlights the importance of understanding the true error rate. For more information, read my blog post: P Values and the Replication of Experiments .

The American Statistical Association speaks out on how to use p-values!

*Thomas SELLKE, M. J. BAYARRI, and James O. BERGER, Calibration of p Values for Testing Precise Null Hypotheses, The American Statistician, February 2001, Vol. 55, No. 1

You Might Also Like

• Trust Center

© 2023 Minitab, LLC. All Rights Reserved.

• Terms of Use
• Privacy Policy
• Cookies Settings

• Prompt Library
• DS/AI Trends
• Stats Tools
• Interview Questions
• Generative AI
• Machine Learning
• Deep Learning

P-Value & Hypothesis Testing: Examples

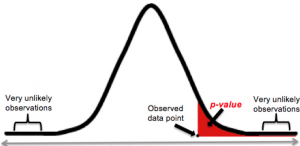
Many describe p-value as the probability that the null hypothesis holds good. That is an incorrect definition. The concept of p-value is understood differently by different people and is considered as one of the most used & abused concepts in statistics, mostly in relation to hypothesis testing. In this blog post, you will learn the P-VALUE concepts with multiple different examples. It is extremely important to get a good understanding of P-value if you are starting to learn data science / machine learning as the concepts of P-value are key to hypothesis testing .

Before getting into the description of p-value, let’s quickly go through the hypothesis testing concepts to get a good understanding.

Table of Contents

What is Hypothesis Testing?

Hypothesis testing can be defined as the statistical framework which can be used to test whether the claim made about anything is true or otherwise. Take a look at the examples of the following claim. This will require hypothesis testing.

• Students of class X studying for more than 6 hours a day on average secures more than 75% marks.
• Anyone walking more than 4 km for 30 consecutive days will lose more than 2 kg weight.

Hypothesis testing requires the formulation of the null hypothesis  and the  alternate hypothesis.  The null hypothesis represents the default state of belief in the real world. For example, the coin is fair. Or, the dice is fair. The alternate hypothesis represents something different and unexpected. The following represent key steps in hypothesis testing. Note the usage of p-value:

• Formulate the null and alternative hypotheses.
• Define the test statistic (such as z-value, or, t-value) that summarizes the strength of evidence against the null hypothesis.
• Determine the appropriate level of significance (0.1, 0.05, or 0.01)
• Compute the p-value that quantifies the probability of having obtained a comparable or more extreme value of the test statistic given that the null hypothesis is true.
• Based on the p-value and level of significance , decide whether the test outcome is statistically significant and hence reject the null hypothesis or otherwise.

A detailed explanation is provided in one of my related posts titled  hypothesis testing explained with examples .

What is P-VALUE?

In hypothesis testing, once the test statistics are determined to evaluate the null hypothesis, the next step is to compute the probability of observing a test statistic as extreme, under the assumption that the null hypothesis Ho is true. This probability is called the P-value. If the value of p-value is smaller than the level of significance, it provides evidence against the null hypothesis. For example, let’s say we are testing the claim that the students studying more than 6 hours on average get more than 75% marks. Here are the steps followed:

• The null hypothesis is that there is no relationship between students for more than 6 hours a day on average and them getting more than 75% marks.
• The data sample for 30 students is gathered.
• Test statistics is t-value and the level of significance is set as 0.05.
• The mean of 30 students is found to be 79% with a standard deviation of 4%
• T-value comes out to be +5.48.
• P-value comes out to be less than 0.00001.
• As the p-value is less than the significance level of 0.05, the test outcome is statistically significant.
• The null hypothesis can thus be rejected. Thus, based on the evidence, the claim can be accepted that students studying more than 6 hours a day on average score more than 75%.

The p-value can be defined as the probability of obtaining test statistics more extreme than the ones observed if we repeated the experiment many many times, provided the null hypothesis holds good.

It is measured using techniques such as determining the test statistics such as Z, T, or chi-square and calculating P-value using the related distribution tables such as z-distribution, t-distribution, or chi-square distribution respectively. The distribution of the test statistic for null hypothesis testing will depend on the details of what type of null hypothesis is being tested, and what type of test statistic is used. In general, most commonly-used test statistics follow a well-known statistical distribution under the null hypothesis — such as a normal distribution, at-distribution, a χ2-distribution, or an F-distribution.

P-VALUE explained with Examples

The examples below do not take into consideration the test statistics and p-value for explaining whether the null hypothesis can be rejected or otherwise. These examples however intend to explain the concepts regarding the p-value and the notion regarding rejecting or failing to reject the null hypothesis.

Let’s take a quick example to understand the concept of P-value. Given the co-ed school consisting of both boys and girls students, let’s test the hypothesis that the boys on average always score a greater percentage of marks than girls in the school . In order to test the hypothesis, as a first step, we will need to formulate the null and alternate hypotheses .

• Null hypothesis: The null hypothesis is the fact that it is not true that boys on average always score a greater percentage of marks than girls.
• Alternate hypothesis: The alternate hypothesis is that the boys on average always score a greater percentage of marks than girls. As part of the test, several random samples of 30 students are taken comprising of both boys.

Out of 10 different samples of 30 students taken comprising of both boys and girls, in 6 samples, the boys on average were found to score a greater percentage of marks than girls. Do we have enough evidence to reject the null hypothesis? It does not look like that. In case, out of 10 samples, in 9 samples, the boys would have been found to score the greater marks than girls, this would not have been a likely result given the null hypothesis is true. Thus, we would have rejected the null hypothesis in favor of the alternate hypothesis – the claim we made in the beginning. However, given that only 6 samples are found where the boys on average scored greater marks than girls, we do have some evidence but not enough to reject the null hypothesis. In this scenario, we will fail to reject the null hypothesis.

The P-VALUE is used to represent whether the outcome of a hypothesis test is statistically significant enough to be able to reject the null hypothesis. It lies between 0 and 1.

The threshold value below which the P-VALUE becomes statistically significant is usually set to be 0.05. The threshold value is called the level of significance and is a function of confidence level.  One could choose to set different threshold values (such as 0.025 or 0.01) based on the confidence level based on which one could choose to reject the null hypothesis. A detailed explanation on significance level is provided in one of my related posts titled Level of significance and hypothesis testing .

The following diagram represents the p-value of the test statistics as the area of the shaded region (with red).

Figure 1. P-Value

P-Value Explained using Null Hypothesis: The Coin is Fair

In case a coin is fair, it is expected that the probability of heads and tails being rolled out is around (or near to) 50%. In order to prove the claim for the population, multiple different experiments with samples representing 10 tosses of coins are done. The null hypothesis is that the coin is fair. The alternate hypothesis is that the coin is unfair. The following represents the test outcomes and interpretation related to when the hypothesis can be rejected.

In the above example, the tests with a number of heads counted as 9 and 1 (red) in a random sample of 10 tosses are at an extreme level. The test outcomes look to be significant enough to indicate that the test results do not look to have happened by chance and that it is incorrect to claim that the coin is fair.  In such cases, the P-Value may/will turn out to be lesser than 0.05. Given that the level of significance is set to be 0.05, the P-value can be used to indicate that the null hypothesis can be rejected. Thus, one could reject the null hypothesis.

P-Value Explained using Null Hypothesis: The Dice is Fair

In case the dice is fair, it is expected that the probability of getting 6 when the dice is rolled out is around (or near to) 16.67% (Expected value – the probability of 1/6). In order to prove the claim for the population, multiple different experiments with samples representing 50 tosses of dice are done. The null hypothesis is that the dice are fair. The alternate hypothesis is that the dice are unfair. The following represents the test outcomes and interpretation related to when the hypothesis can be rejected.

In the above example, the tests with a number of 6s counted as 3 and 48 (red) in a random sample of 50 tosses are at an extreme level. The test outcomes look to be significant enough to indicate that the test results do not look to have happened by chance and that it is incorrect to claim that the dice are fair.  In such cases, the P-Value may/will turn out to be lesser than 0.05. Given that the level of significance is set to be 0.05, the P-value can be used to indicate that the null hypothesis can be rejected. Thus, one could reject the null hypothesis.

• P-Value (Wikipedia)

In this post, you learned about what is P-Value with the help of examples . Understanding P-Value is important for Data Scientists as it is used for hypothesis testing related to whether there is a relationship between a response variable and predictor variables. Hope you liked the details presented in the post. Please leave your comments or feel free to suggest.

Recent Posts

• Self-Supervised Learning: Concepts, Examples - August 20, 2024
• MSE vs RMSE vs MAE vs MAPE vs R-Squared: When to Use? - August 18, 2024
• K-Fold Cross Validation in Machine Learning – Python Example - August 16, 2024

Ajitesh Kumar

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

• Search for:

ChatGPT Prompts (250+)

• Generate Design Ideas for App
• Expand Feature Set of App
• Create a User Journey Map for App
• Generate Visual Design Ideas for App
• Generate a List of Competitors for App
• Self-Supervised Learning: Concepts, Examples
• MSE vs RMSE vs MAE vs MAPE vs R-Squared: When to Use?
• K-Fold Cross Validation in Machine Learning – Python Example
• Gradient Boosting Machines (GBM): Concepts, Examples
• Random Forest Classifier – Sklearn Python Example

Data Science / AI Trends

• • Prepend any arxiv.org link with talk2 to load the paper into a responsive chat application
• • Custom LLM and AI Agents (RAG) On Structured + Unstructured Data - AI Brain For Your Organization
• • Guides, papers, lecture, notebooks and resources for prompt engineering
• • Common tricks to make LLMs efficient and stable
• • Machine learning in finance

Free Online Tools

• Create Scatter Plots Online for your Excel Data
• Histogram / Frequency Distribution Creation Tool
• Online Pie Chart Maker Tool
• Z-test vs T-test Decision Tool
• Independent samples t-test calculator

Recent Comments

I found it very helpful. However the differences are not too understandable for me

Very Nice Explaination. Thankyiu very much,

in your case E respresent Member or Oraganization which include on e or more peers?

Such a informative post. Keep it up

Thank you....for your support. you given a good solution for me.

• Math Article

In Statistics, the researcher checks the significance of the observed result, which is known as test static . For this test, a hypothesis test is also utilized. The P-value  or probability value concept is used everywhere in statistical analysis. It determines the statistical significance and the measure of significance testing. In this article, let us discuss its definition, formula, table, interpretation and how to use P-value to find the significance level etc. in detail.

Table of Contents:

P-value Definition

The P-value is known as the probability value. It is defined as the probability of getting a result that is either the same or more extreme than the actual observations. The P-value is known as the level of marginal significance within the hypothesis testing that represents the probability of occurrence of the given event. The P-value is used as an alternative to the rejection point to provide the least significance at which the null hypothesis would be rejected. If the P-value is small, then there is stronger evidence in favour of the alternative hypothesis.

P-value Table

The P-value table shows the hypothesis interpretations:

Generally, the level of statistical significance is often expressed in p-value and the range between 0 and 1. The smaller the p-value, the stronger the evidence and hence, the result should be statistically significant. Hence, the rejection of the null hypothesis is highly possible, as the p-value becomes smaller.

Let us look at an example to better comprehend the concept of P-value.

Let’s say a researcher flips a coin ten times with the null hypothesis that it is fair. The total number of heads is the test statistic, which is two-tailed. Assume the researcher notices alternating heads and tails on each flip (HTHTHTHTHT). As this is the predicted number of heads, the test statistic is 5 and the p-value is 1 (totally unexceptional).

Assume that the test statistic for this research was the “number of alternations” (i.e., the number of times H followed T or T followed H), which is two-tailed once again. This would result in a test statistic of 9, which is extremely high and has a p-value of 1/2 8 = 1/256, or roughly 0.0039. This would be regarded as extremely significant, much beyond the 0.05 level. These findings suggest that the data set is exceedingly improbable to have happened by random in terms of one test statistic, yet they do not imply that the coin is biased towards heads or tails.

The data have a high p-value according to the first test statistic, indicating that the number of heads observed is not impossible. The data have a low p-value according to the second test statistic, indicating that the pattern of flips observed is extremely unlikely. There is no “alternative hypothesis,” (therefore only the null hypothesis can be rejected), and such evidence could have a variety of explanations – the data could be falsified, or the coin could have been flipped by a magician who purposefully swapped outcomes.

This example shows that the p-value is entirely dependent on the test statistic used and that p-values can only be used to reject a null hypothesis, not to explore an alternate hypothesis.

P-value Formula

We Know that P-value is a statistical measure, that helps to determine whether the hypothesis is correct or not. P-value is a number that lies between 0 and 1. The level of significance(α) is a predefined threshold that should be set by the researcher. It is generally fixed as 0.05. The formula for the calculation for P-value is

Step 1: Find out the test static Z is

P0 = assumed population proportion in the null hypothesis

N = sample size

Step 2: Look at the Z-table to find the corresponding level of P from the z value obtained.

P-Value Example

An example to find the P-value is given here.

Question: A statistician wants to test the hypothesis H 0 : μ = 120 using the alternative hypothesis Hα: μ > 120 and assuming that α = 0.05. For that, he took the sample values as

n =40, σ = 32.17 and x̄ = 105.37. Determine the conclusion for this hypothesis?

We know that,

Now substitute the given values

Now, using the test static formula, we get

t = (105.37 – 120) / 5.0865

Therefore, t = -2.8762

Using the Z-Score table , we can find the value of P(t>-2.8762)

From the table, we get

P (t<-2.8762) = P(t>2.8762) = 0.003

If P(t>-2.8762) =1- 0.003 =0.997

P- value =0.997 > 0.05

Therefore, from the conclusion, if p>0.05, the null hypothesis is accepted or fails to reject.

Hence, the conclusion is “fails to reject H 0. ”

Frequently Asked Questions on P-Value

What is meant by p-value.

The p-value is defined as the probability of obtaining the result at least as extreme as the observed result of a statistical hypothesis test, assuming that the null hypothesis is true.

What does a smaller P-value represent?

The smaller the p-value, the greater the statistical significance of the observed difference, which results in the rejection of the null hypothesis in favour of alternative hypotheses.

What does the p-value greater than 0.05 represent?

If the p-value is greater than 0.05, then the result is not statistically significant.

Can the p-value be greater than 1?

P-value means probability value, which tells you the probability of achieving the result under a certain hypothesis. Since it is a probability, its value ranges between 0 and 1, and it cannot exceed 1.

What does the p-value less than 0.05 represent?

If the p-value is less than 0.05, then the result is statistically significant, and hence we can reject the null hypothesis in favour of the alternative hypothesis.

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

P-value Formula 

The P-value formula is short for probability value. P-value defines the probability of getting a result that is either the same or more extreme than the other actual observations. The P-value represents the probability of occurrence of the given event. The P-value formula is used as an alternative to the rejection point to provide the least significance for which the null hypothesis would be rejected. The smaller the P-value, the stronger is the evidence in favor of the alternative hypothesis given observed frequency and expected frequency. 

What is P-value Formula?

P-value is an important statistical measure, that helps to determine whether the hypothesis is correct or not. P-value always only lies between 0 and 1. The level of significance(α) is a predefined threshold that should be set by the researcher. It is generally fixed as 0.05. The formula for the calculation for P-value is:

Step 1: Find out the test static Z is

\(Z = \frac{\hat{p}-p 0}{\sqrt{\frac{p 0(1-p 0)}{n}}}\)

• \(\hat{p}=\)Sample Proportion
• \(\mathrm{P0}=\) assumed population proportion in the null hypothesis
• N = sample size

Step 2: Look at the Z-table to find the corresponding level of P from the z value obtained.

P-value Formula

The formula to calculate the P-value is:

\(\hat{p}=\)Sample Proportion \(\mathrm{P0}=\) assumed population proportion in the null hypothesis

P-value Table

The below-mentioned P-value table helps in determining the hypothesis according to the p-value. 

P-value ≤ 0.05	It indicates the null hypothesis is very unlikely.   It indicates the null hypothesis is very likely. Book a Free Trial Class Examples Using P-value Formula  Example 1: A statistician is testing the hypothesis H0: μ = 120 using the approach of alternative hypothesis Hα: μ > 120 and assuming that α = 0.05. The sample values that he took are as n =40, σ = 32.17 and x̄ = 105.37. What is the conclusion for this hypothesis? We know that, \(\sigma_{\bar{x}}=\dfrac{\sigma}{\sqrt{n}}\) Now substitute the given values \(\sigma_{\bar{x}}=\dfrac{32.17}{\sqrt{40}}=5.0865\) As per the test static formula, we get t = (105.37 – 120) / 5.0865 Therefore, t = -2.8762 Using the Z-Score table, finding the value of P(t > -2.8762) P (t < -2.8762) = P(t > 2.8762) = 0.003 If P(t > -2.8762) =1 - 0.003 =0.997 P- value =0.997 > 0.05 As the value of p > 0.05, the null hypothesis is accepted. Therefore, the null hypothesis is accepted. Example 2: P-value is 0.3105. If the level of significance is 5%, find if we can reject the null hypothesis. Solution: Looking at the P-value table, the p-value of 0.3105 is greater than the level of significance of 0.05 (5%), we fail to reject the null hypothesis. Example 3: P-value is 0.0219. If the level of significance is 5%, find if we can reject the null hypothesis. Solution: Looking at the P-value table,   the p-value of 0.0219 is less than the level of significance of 0.05, we reject the null hypothesis. FAQs on P-value Formula  What is meant by p-value formula. The P-value formula is short for probability value. P-value defines the probability of getting a result that is either the same or more extreme than the other actual observations. The P-value represents the probability of occurrence of the given event. The formula to calculate the p-value is: \(Z = \frac{\hat{p}-p 0}{\sqrt{\frac{p 0(1-p 0)}{n}}}\) What is the Formula to Calculate the P-value? What is the p-value formula table . The P-value formula table is:  Using the P-value Formula Table, Check if the Hypothesis is Rejected or not when the P-value is 0.354 with 5% Level of Significance. Looking at the table, the p-value of 0.354 is greater than the level of significance of 0.05 (5%), we fail to reject the null hypothesis. Skip to secondary menu Skip to main content Skip to primary sidebar Statistics By Jim Making statistics intuitive P-Values, Error Rates, and False Positives By Jim Frost 41 Comments In my post about how to interpret p-values , I emphasize that p-values are not an error rate. The number one misinterpretation of p-values is that they are the probability of the null hypothesis being correct. The correct interpretation is that p-values indicate the probability of observing your sample data, or more extreme, when you assume the null hypothesis is true. If you don’t solidly grasp that correct interpretation, please take a moment to read that post first. Hopefully, that’s clear. Unfortunately, one part of that blog post confuses some readers. In that post, I explain how p-values are not a probability, or error rate, of a hypothesis. I then show how that misinterpretation is dangerous because it overstates the evidence against the null hypothesis. The logical question is, if p-values aren’t an error rate, how can you report those higher false positive rates (an error rate)? That’s a reasonable question and it’s the topic of this post! A Quick Note about This Post This post might be a bit of a mind-bender. P-values are already confusing! And in this post, we look at p-values differently using a different branch of statistics and methodology. I’ve hesitated writing this post because it feels like a deep, dark rabbit hole! However, the ideas from this exploration of p-values have strongly influenced how I view and use p-values. While I’m writing this post after other posts and an entire book chapter about p-values, the line of reasoning I present here strongly influenced how I wrote that earlier content. Buckle up! Frequentist Statistics Before calculating the false positive rate, you need to understand frequentist statistics, also known as frequentist inference. Frequentist statistics are what you learned, or are learning, in your Introduction to Statistics course. This methodology is a type of inferential statistics containing the familiar hypothesis testing framework where you compare your p-values to the significance level to determine statistical significance. It also includes using confidence intervals to estimate effects. Frequentist inference focuses on frequencies that make it possible to use samples to draw conclusions about entire populations. The frequencies in question are the sampling distributions of test statistics. That goes beyond the scope of this post but click the related posts links below for the details. Frequentist methodology treats population parameters , such as the population mean (µ), as fixed but unknown characteristics. There are no probabilities associated with them. The null and alternative hypotheses are statements about population parameters. Consequently, frequentists can’t say that there is such and such probability that the null hypothesis is correct. It either is correct or incorrect, but you don’t know the answer. The relevant point here is that when you stick strictly to frequentist statistics, there is no way to calculate the probability that a hypothesis is correct. Related posts : How Hypothesis Tests Work , How t-Tests Work , How F-tests Work in ANOVA , and How the Chi-Squared Test of Independence Works Why Can’t Frequentists Calculate those Probabilities? There are mathematical reasons for that but let’s look at it intuitively. In frequentist inference, you take a single, random sample and draw conclusions about the population. The procedure does not use other information from the outside world or other studies. It’s all based on that single sample with no broader context. In that setting, it’s just not possible to know the probability that a hypothesis is correct without incorporating other information. There’s no way to tell whether your sample is unusual or representative. Frequentist methods have no way to include such information and, therefore, cannot calculate the probability that a hypothesis is correct. However, Bayesian statistics and simulation studies include additional information. Those are large areas of study, so I’ll only discuss the points relevant to our discussion. Bayesian Statistics Bayesian statistics can incorporate an entire framework of evidence that resides outside the sample. Does the overall fact pattern support a particular hypothesis? Does the larger picture indicate that a hypothesis is more likely to be correct before starting your study? This additional information helps you calculate probabilities for a hypothesis because it’s not limited to a single sample. Simulation Studies When you perform a study in the real world, you do it just once. However, simulation studies allow statisticians to perform simulated studies thousands of times while changing the conditions. Importantly, you know the correct results, enabling you to calculate error rates, such as the false positive rate. Using frequentist methods, you can’t calculate error rates for hypotheses. There is no way to take a p-value and convert it to an error rate. It’s just not possible with the math behind frequentist statistics. However, by incorporating Bayesian and simulation methods, we can estimate error rates for p-values. Simulation Studies and False Positives In my post about interpreting p-values, I quote the results from Sellke et al. He used a Bayesian approach. But let’s start with simulation studies and see how they can help us understand the false positive rate. For this, we’ll look at the work of David Colquhoun, a professor in biostatistics, who lays it out here . Factors that influence the false-positive rate include the following: Prevalence of real effects (higher is good) Power (higher is good) Significance level (lower is good) “Good” indicates the conditions under which hypothesis tests are less likely to produce false positives. Click the links to learn more about each concept. The prevalence of real effects indicates the probability that an effect exists in the population before conducting your study. More on that later! Let’s see how to calculate the false positive rate for a particular set of conditions. Our scenario uses the following conditions: Prevalence of real effects = 0.1 Significance level (alpha) = 0.05 Power = 80% We’ll “perform” 1000 hypothesis tests under these conditions. In this scenario, the total number of positive test results are 45 + 80 = 125. However, 45 of those positives are false. Consequently, the false positive rate is: Mathematically, calculate the false positive rate using the following: Where alpha is your significance level and P(real) is the prevalence of real effects. Simulation studies for P-values The previous example and calculation incorporate the significance level to derive the false positive rate. However, we’re interested in p-values. That’s were the simulation studies come in! Using simulation methodology, Colquhoun runs studies many times and sets the values of the parameters above. He then focuses on the simulated studies that produce p-values between 0.045 and 0.05 and evaluates how many are false positives. For these studies, he estimates a false positive rate of at least 26%. The 26% error rate assumes the prevalence of real effects is 0.5, and power is 80%. Decreasing the prevalence to 0.1 causes the false positive rate to jump to 76%. Yikes! Let’s examine the prevalence of real effects more closely. As you saw, it can dramatically influence the error rate! P-Values and the Bayesian Prior Probability The property that Colquhoun names the prevalence of real effects (P(real)) is what the Bayesian approach refers to as the prior probability. It is the proportion of studies where a similar effect is present. In other words, the alternative hypothesis is correct. The researchers don’t know this, of course, but sometimes you have an idea. You can think of it as the plausibility of the alternative hypothesis. When your alternative hypothesis is implausible, or similar studies have rarely found an effect, the prior probability (P(real)) is low. For instance, a prevalence of 0.1 signifies that 10% of comparable alternative hypotheses were correct, while 90% of the null hypotheses were accurate (1 – 0.1 = 0.9). In this case, the alternative hypothesis is unusual, untested, or otherwise unlikely to be correct. When your alternative hypothesis is consistent with current theory, has a recognized process for producing the effect, or prior studies have already found significant results, the prior probability is higher. For instance, a prevalence of 0.90 suggests that the alternative is correct 90% of the time, while the null is right only 10% of the time. Your alternative hypothesis is plausible. When the prior probability is 0.5, you have a 50/50 chance that either the null or alternative hypothesis is correct at the beginning of the study. You never know this prior probability for sure, but theory, previous studies, and other information can give you clues. For this blog post, I’ll assess prior probabilities to see how they impact our interpretation of P values. Specifically, I’ll focus on the likelihood that the null hypothesis is correct (1 – P(real)) at the start of the study. When you have a high probability that the null is right, your alternative hypothesis is unlikely. Moving from the Prior Probability to the Posterior Probability From a Bayesian perspective, studies begin with varying probabilities that the null hypothesis is correct, depending on the alternative hypothesis’s plausibility. This prior probability affects the likelihood the null is valid at the end of the study, the posterior probability. If P(real) = 0.9, there is only a 10% probability that the null is correct at the start. Therefore, the chance that the hypothesis test rejects a true null at the end of the study cannot be greater than 10%. However, if the study begins with a 90% probability that the null is right, the likelihood of rejecting a true null escalates because there are more true nulls. The following table uses Colquhoun and Sellke  et al.’s calculations . Lower prior probabilities are associated with lower posterior probabilities. Additionally, notice how the likelihood that the null is correct decreases from the prior probability to the posterior probability. The precise value of the p-value affects the size of that decrease. Smaller p-values cause a larger decline. Finally, the posterior probability is also the false positive rate in this context because of the following: the low p-values cause the hypothesis test to reject the null. the posterior probability indicates the likelihood that the null is correct even though the hypothesis test rejected it. 0.5 0.05 0.289 0.5 0.01 0.110 0.5 0.001 0.018 0.33 0.05 0.12 0.9 0.05 0.76 Safely Using P-values Many combinations of factors affect the likelihood of rejecting a true null. Don’t try to remember these combinations and false-positive rates. When conducting a study, you probably will have only a vague sense of the prior probability that your null is true! Or maybe no sense of that probability at all! Just keep these two big takeaways in mind: A single study that produces statistically significant test results can provide weak evidence that the null is false, especially when the P value is close to 0.05. Different studies can produce the same p-value but have vastly different false-positive rates. You need to understand the plausibility of the alternative hypothesis. Carl Sagan’s quote embodies the second point, “Extraordinary claims require extraordinary evidence.” Suppose a new study has surprising results that astound scientists. It even has a significant p-value! Don’t trust the alternative hypothesis until another study replicates the results! As the last row of the table shows, a study with an implausible alternative hypothesis and a significant p-value can still have an error rate of 76%! I can hear some of you wondering. Ok, both Bayesian methodology and simulation studies support these points about p-values. But what about empirical research? Does this happen in the real world? A study that looks at the reproducibility of results from real experiments supports it all. Read my post about p-values and the reproducibility of experimental results . I know this post might make p-values seem more confusing. But don’t worry!  I have another post that provides simple recommendations to help you navigate P values. Read my post: Five P-value Tips to Avoid Being Fooled by False Positives . Share this: Reader Interactions July 26, 2024 at 9:47 am Hi Jim, thank you for this very important work of explanation. I have fallen into the rabbit hole of the relationship between p-values and error rates because of some literature review I have been doing in sports science. In this field, researchers often use ANOVA to compare the effect of different training regimens on certain physical ability metrics such as endurance. To test endurance, they come up with tests for which they often don’t evaluate the test-retest reliability. My initial inquiry was: how often can an ANOVA incorrectly detect a difference with p <= 0.05 as a function of test-retest reliabiliyt (measured using an ICC), in other words, how is the error rate affected by measurement (un)reliability? I ended up finding a paper by Westfall and Yarkoni (2016) on the effect of reliability on controlling for confounding variables, but I don't think this translates to my inquiry. That is how I ended up reading your blog posts on p-values which have been very illuminating. However I believe the work you shared doesn't take into account measurement reliability. Would you happen to have some thoughts or references to share on the impact of measurement reliability on the rate of false positives (type I error rate) in ANOVA? Thank you very much. August 1, 2024 at 7:56 pm All hypothesis tests, including ANOVA, assume that measurement error is small compared to the sampling error. If you can’t make that assumption, it raises questions about the results. Hypothesis testing does not account for measurement error, just sampling error. I don’t know of a way to factor in measurement error to the results. It’s not standard practice. Ideally, the researchers would have conducted an assessment of their measurements to make that determination. Unfortunately, I don’t have references on hand. But, if you have concerns about the data’s reliability, that is potentially a legitimate problem and I’d encourage you to look into it more. Sorry I can’t be more helpful with a reference though. June 12, 2022 at 2:55 am Yes but I am not looking for the error rate after the simulation is done. I need a way to control the error rate before the algorithm run. And intuitively there must be a way to do it with a threshold p Value on which you base the decision. The lower the pValue threshold, the better for error rate. I am looking for a way to calculate the function that retrieve error rate from this “beforehand chosen pValue threshold”. The only way I can think for now is to run the simulation with different critical values, observe error rate, and interpolate points to get a continuous function. So I was hoping that you had a better idea. June 9, 2022 at 2:57 am Thanks for this blog. I am not a mathematician, just a computer scientist. Thus I may misunderstand but you seem to say that we cant compute error rate from value. My problem is as follow. I have a set of inputs that follow random distributions. By design, all the distribution are equals except for one that is have a bigger mean (very litle difference). All have same variance. I try to find the quickest way (in amount of try) to isolate this particular input with user given probability x. One of my approach is based on critical pvalues over the difference of the best set of data compared with all the others. I stop when the difference reach a predefined pValue. I was really surprised by the difference between error rate and pvalue observe: pvalue = 0.0025 => 0.14 error rate. This is why I came here to try to understand. It’s clear thanks to you now that this is to be expected, but I still cant grasp that there is no way to link the two values when you control every parameter. Since I am doing simulation, I control every parameter. The prevalence of effect is one. This is really bogging me (I find it counterintuitive), that I cant control x with pValues, but I can using an other interval of trust technique. Specially because the pvalue method go a bit faster: pvalues: (x = 0.859: numberOfTry=127.881) intérvals: (x=0.864, numberOfTry=134.649 So my question is: Is there really nothing to do to anticipate error rate from critical pValue for my specific use case? Do you have recommendation on the best way to resolve my problem ? Ps: the interval technique finish when both sets of data interval and all the other data interval become disjoint. June 12, 2022 at 1:07 am Please understand that when I say you can’t link p-values to error rates, I’m referring to real studies using real data. In those cases, you only get one sample and you don’t know (and can’t control) the population parameters. However, when you’re performing simulation studies, you certainly do control the population parameters and can draw repeated samples from the populations as you define them. In those cases, yes, you can certainly know the error rates because you know all the necessary information. However, in real world studies, you don’t have all that necessary info. That’s a huge difference! March 3, 2022 at 12:40 pm Thanks again, Jim. I have 3 comments: First, you said that the probabilities of the following four events do not sum to 1. I think they DO sum to 1 — it is just that two of them will have probability zero, because, as you said, either the null is true or it is false. So, point taken. 1. Reject a true null hypothesis. 2. Reject a false null hypothesis. 3. Fail to reject a true null hypothesis. 4. Fail to reject a false null hypothesis. Second, I guess I still don’t understand the definition of a Type I error rate, if you say it is hard to determine. I completely understand that the error rate is not equal to the P-value, even though it is in fact a probability — but how is that probability defined? Given what you have written, I don’t see how it is different than alpha. Finally, I was talking about these ideas with a friend, and he referred me to this interesting article. Evidently I am not alone in thinking that Type I errors don’t occur. See page 1000. https://www.sjsu.edu/faculty/gerstman/misc/Cohen1994.pdf The author makes a point that I had never seen before. We are all familiar with this logic: If A, then B; it follows that if B isn’t true, we assume A isn’t true. In our context, ff the null is true, we won’t get this data; we got this data, so the null is false. He then points out how this isn’t quite right, and it is more accurate to say: If the null is true, we probably don’t get this data. We then conclude that if we got this data, the null is probably false. But this is very bad logic, as shown in this example: If a person is an American, he is probably not a member of Congress. Since this person is a member of Congress, he is probably not an American. Such logic falls into the same trap of thinking that Prob(getting this sample data, given that the null is true) is equal to Prob(the null is true, given this sample data). March 3, 2022 at 2:10 pm We’re getting to the point where we’re going around in circles a bit. If you have questions after this reply, please use my contact me form. I’ll try not to be too repetitive below because I’ve addressed several of these points already. I suppose you could say that all four should sum to 1. However, only two of them will be valid for any given test. In my list below, only 1 & 2 or 3 & 4 will be valid possibilities for a given test. And, again, you should be listing them in a logical order like the following where you correctly group complementary pairs. The order you use doesn’t emphasize the natural pairings. 1. Reject a true null: error rate = α 2. Failing to reject a true null: correct decision rate = 1 – α. 3. Failing to reject a false null: error rate = β 4. Reject a false null: correct decision rate = 1 – β (aka statistical power) While you could say the invalid pair has a probability that sums to zero, it doesn’t really make sense to consider, say, the probability of rejecting a true null for a test where the null is false. Of course, you don’t know the answer to that, but in theory that’s the case. But, if you want to consider one pair to have a probability of zero and the other pair to have a probability of 1, I suppose that works. Maybe it even clarifies how one pair is invalid. I focus on the interpretation of p-values . Click the link to read. I specifically cover what the probability represents. And read the following for graphical comparison between significance levels and p-values . I’ve already covered in detail in my previous replies why it’s not a problem if type I errors don’t exist. I have heard of this thinking before, but I don’t buy it personally. It’s easy enough to imagine a totally ineffective treatment where both populations are by definition the same. But, even if you assume that there is always some minimal effect, it’s not a problem for all the reasons I explained before. Then it just becomes a case of having a large enough sample size to detect meaningful effects and to produce a sufficiently precise confidence interval. That’s already built into the power analysis process. So, even if you’re right, it’s a not a problem. I do want to address your logic example. I actually addressed this idea in a previous reply. Yes, that is bad logic. And hypothesis testing specifically addresses that. That’s why when your results are not significant, we say that you “fail to reject the null.” You are NOT accepting the null. A non-significant hypothesis test isn’t proving that there is no effect (i.e., not proving the null is true). Instead, it’s saying that you have insufficient evidence to conclude that an effect exists in the population. Similar to your logic example, that is NOT the same as saying there is no effect. I’ve written a post about that topic exactly. I included in a previous reply, and I suggest you read it this time! 🙂 Failing to Reject the Null Hypothesis . February 25, 2022 at 12:07 pm Wait, one more post. Perhaps I just had an epiphany. By the error rate of “rejecting a true null”, do you mean the probability that the null is true, given that we rejected it? And this is what can be has high as 0.23 when P = .05 ? This is in contrast to the probability of a Type I error, alpha, which is the probability of rejecting a null, given that it is true? If this is what is meant, then my confusion is removed, and it explains why the error rate and alpha are not equal — they are different conditional probabilities. Of course these two probabilities are related to each other via Baye’s Theorem. By the way, if this is correct, then I change my initial objection from Type I errors hardly ever occurring to claim that the error rate is almost always 0, since the null is hardly ever true, unless we have some error tolerance built into the statement of the null :). March 1, 2022 at 1:16 am Type I errors can only occur when the null is true by definition. You’re rejecting a null that is true. That’s an error and can, obviously, only occur when the null is true. When the null is false, you can’t reject it incorrectly. The p-value error rate is also the same idea. You can only incorrectly reject the null when the null is true. So, yes, both cases are conditional on a true null. You can’t incorrectly reject a false null. As I write in my other reply, The type I error rate equals the significance level and applies to a range of p-values for a class of studies. For individual p-values from a single study, you need to use other methodologies just to estimate the false positive error rate. February 25, 2022 at 9:07 am Maybe we should continue, if you are willing, to do this via private email. I feel I have hijacked your thread here! So, I’ll just give one last response. My point was that those four scenarios partition the space of outcomes from experiments, so all four should add up to 1, and it doesn’t matter what order we list them. If we want to look at the probability that we make an error, in my list we can add them: P(error) = P(Case 1) + P(Case 4). In your list, you have written them as conditional probabilities, so they can’t be added. The probability of making an error is not α + β. This is why when errors type I and Type II errors are discussed, I think they should ALWAYS be described as conditional probabilities. To me, saying “rejecting a true null” is too likely to be interpreted as “rejecting and true null” rather than “rejecting | true null”. I’ve read your other pieces, and want to make sure I understand something. Above, you say the Type I error rate is simply α. However, in the article, you say the Type I error rate can be as high as 23% when P = 0.05. Does this just mean that apriori the error rate is α, but after you take your sample and get P=.05, you have new information, and the error rate has now climbed to 0.23? Thanks again. March 1, 2022 at 1:08 am I think this is a good discussion that others will benefit from. That’s why I always prefer discussion in the comments rather than via email! But that’s not correct thinking that those four scenarios should sum to 1. Perhaps we need to teach that better. However, the null hypothesis is either true or false. We don’t know the answer, but we do know that it’s one or the other. When the null is false, there is no chance of a false negative. And when the null is true, there is no chance of a false positive. I show two distribution curves in my post about the types of error. In actuality, only one of those curves exist, we just don’t know which one. As you say, they are conditional probabilities. Although, I think that’s baked right into the names as I’ve mentioned, but I can see the need to emphasize it. Getting to your questions about the error, there are a few complications! For one thing, the type I error rate equals the significance level (α), which applies to a range of p-values. Using frequentist methodology, there is no way to obtain an error rate for a single p-value from a study. However, using other methodologies, such as Bayesian statistics and simulation studies, you can estimate error rates for individual p-values. You do need to make some assumptions but it’s possible to come up with ballpark figures. And when I talk about error rates as high as 23% for a p-value of 0.05, it’s using those other methodologies. That’s why I consider a p-value around 0.05 (either above or below) to be fairly weak evidence on their own. I think I use an a priori probability of 0.5 for whether the null is true for the 23%. Obviously, the false positive rate will be higher when that probability is higher. But there was no reason to have assumed that a p-value of 0.05 should produce an error rate of 0.05 to begin with. That’s the common misinterpretation I discuss in my article about interpreting p-values. Many people link p-values to that type of error rate, but it’s just not true. And my point is that using conservative a priori probabilities, you can see that the true error rate is typically higher. Again, the Type I error rate equals the significance level, not an individual p-value. February 24, 2022 at 9:45 pm You wrote: “I still don’t quite understand what you’re saying about the vagueness of the Type I error rate. The type I error rate is the probability of rejecting a true null hypothesis. Therefore, by definition we’re talking about cases where the null hypothesis is correct.” This is what I meant. There are four non-overlapping possibilities, each with its own probability. 1. Reject a true null hypothesis. 2. Reject a false null hypothesis. 3. Fail to reject a true null hypothesis. 4. Fail to reject a false null hypothesis. It would be reasonable for one to conclude that the sum of these four probabilities is 1. However, when you say that the Type 1 error rate is the probability of rejecting a true null hypothesis, you actually mean the sum of the probabilities in 1 and 3 equals 1, and that the error rate is P(1)/( P(1) + P(3) ). February 25, 2022 at 3:05 am I guess if you write the list in that particular order, you’d need to sum non-adjacent items. Consequently, I wouldn’t list them in that order. It’s more logical to group them by whether the null hypothesis is true or not rather than by the rejection decision. But I do agree that we need to be clear when teaching this subject! 1. Reject a true null: error rate = α 2. Failing to reject a true null: correct decision rate = 1 – α. 3. Failing to reject a false null: error rate = β 4. Reject a false null: correct decision rate = 1 – β (aka statistical power) For more information on this topic, read my post about the two types of error in hypothesis testing . In that post, I put these in a table and I also show them on sampling distributions. February 24, 2022 at 8:10 am I completely resonate with what you say here. In fact, I’ve long thought that hypotheses should actually have an error tolerance built into them that somehow includes the effect size that is considered negligible. For example, it should be stated as an interval: mu = 100 +/- 1, if all values of mu in that range would be considered indistinguishable in any practical sense for the given context. Of course, this would make the calculation of the P-value a bit more complicated, and one would have to assume some type of distribution of the values of the parameter (probably normal or uniform) within the interval, but with technology this wouldn’t be a problem. I have never actually taken the step to see what effect such an approach would have on the P-values. Maybe none. Finally, I didn’t mean to imply that I think the definition of a Type I error is vague — I agree it is well-defined. What I meant is that I think that when the probability of a Type I error is discussed, we could all do a better job of clarifying that the sample space is all experiments for which the null is true. (Of course, that gets me back to my earlier issue, because I think the sample space is so small!) Thank you again for your responses. I want to read some of your other articles. I’m a mathematician who teaches statistics, and this is all very helpful to me. February 24, 2022 at 5:15 pm There is actually a standard way of doing just that. It involves using confidence intervals to evaluate both the magnitude and precision of the estimate effect. For more details, read my post about practical vs statistical significance . The nice thing is that CI approach is entirely consistent with p-values. I still don’t quite understand what you’re saying about the vagueness of the Type I error rate. The type I error rate is the probability of rejecting a true null hypothesis. Therefore, by definition we’re talking about cases where the null hypothesis is correct. And, even if that sample space is small, it’s not really a problem. Thanks for the interesting discussion! February 23, 2022 at 9:54 pm Thank you for the comment. That is a good point about the possibility of the null hypothesis being true with an equal sign for two-sample tests when considering the effect of a bogus drug. I guess I was mostly thinking of one-sample tests with a fixed standard in the null. Having said that, in your example, yes, it is easy to believe in a theoretically worthless treatment. In practice, if every subject of the population were tested (i.e., our sample is the population), an effect would likely always be observed, however small it is. In this case, then, it seems we probably need to define exactly what we mean when we refer to a population. To make my case (that the null is never true), I would define the population as an actual group of subjects who could conceivably be tested, not as an idealized theoretical group of all possible subjects. It seems the logic is backwards to say “The treatment is worthless, so the parameter must exactly equal zero.” On my other point, I realize that “probability of rejecting a null hypothesis that is true” is the usual definition. But I find this to be vague, because it can logically be interpreted by students as the probability of the intersection of two events: (1) Rejecting the null, and (2) The null is true. That is a very different than the conditional probability of Rejecting the null given that the null is true. I do realize these comments of mine are a bit pedantic. However, they have troubled me for some time, so I appreciate having your ear for a moment! February 23, 2022 at 10:45 pm For the sake of discussion, let’s go beyond the question of whether the null can be true exactly or not but ponder only those cases where it’s not exactly true but close. We’ll assume those cases exist to one degree or another even if we’re not sure how often. In those cases, it’s still not a problem. If the null is always false to some degree, then you don’t need to worry about Type I errors because that deals with true nulls. Instead, you’re worrying about Type II errors (failing to reject a false null) because that is applicable to false nulls. An effect exists but the test is not catching it. That sounds like a problem, but it isn’t necessarily. If the true population effect exists but is trivial, it’s not a problem if you fail to detect it. When you fail to reject the null in that case, you’re not missing out on an important finding. In fact, when you perform a power analysis before a test, you need to know the minimum effect size that is not trivial. This process helps you obtain a large enough sample so you have reasonable chance of detecting an effect that you’d consider important if it exists. (It also prevents you from obtain such a large sample size that you’ll detect a trivial effect.) In this scenario, you just want to have a reasonable chance of detecting an effect that is important. If you fail to reject the null in this case, it doesn’t matter whether the null is true or minimally false. In a practical sense that doesn’t matter. And remember, failing to reject the null doesn’t mean you’re proving the null is true. You can read my article about why we use the convoluted wording of failing to reject the null . So, in the scenario you describe, you wouldn’t worry about type I errors, only type II. And in that context, you want to detect important effects but it’s fine to fail to detect trivial effects. And that comes down to power analysis. I probably made that as clear as mud, but I hope you get my point. To learn more about how and why a power analysis builds in the idea of a practically significant effect size, read my post about power analysis . Finally, I don’t think the definition of a type I error is vague at all (or type II). They’re very specific. “It’s an error if you reject a null hypothesis that is true.” That statement is true by definition and has very precise meaning in the context of a hypothesis test where you define the null hypothesis. It’s certainly true that students can misinterpret that but that’s a point of education rather than a vague definition. It is an interesting discussion! February 23, 2022 at 10:38 am Could you clarify what you mean by the error rate? I think you said it is the conditional probability of Rejecting the null, given that the null is true? However, the null hypothesis is actually NEVER true if when we write = we really mean equal. It might be very close to being true, or it might be true to the level of precision with which we can measure, but it won’t actually be true. (In the same way that no matter how many decimals someone gives me for the value of the number pi, the value they give will still not actually equal pi.) However, in our hypotheses, we do not stipulate the level of accuracy for which we need to agree that two numbers are equal. So, my question: How does it make sense to talk about the conditional probability of an event when the underlying condition never happens? February 23, 2022 at 8:55 pm That’s correct that the error rate, more specifically, the Type I error rate, is the probability of rejecting a null hypothesis that is true. However, I’d disagree that the null hypothesis is never true when using an equal sign. For example, imagine that you’re testing a medication that truly is worthless. It has no effect whatsoever. If you perform an experiment with a treatment and control group, the null hypothesis is that the outcomes for the treatment group equals the control group. If the medication truly has zero effect, then at the population level, the outcomes should be equal. Of course, your sample means are unlikely to be exactly equal due to random sampling error. However, I would agree that there are many cases where, using the medication example, it has some effect but not a practically meaningful effect. In that case, the null hypothesis is not correct. But that’s not a problem. If you reject the null hypothesis when the treatment group is marginally better than the control group, it’s not an error. The hypothesis test made the correct decision by rejecting the null. At that point, it becomes a distinction between statistical significance and practical significance (i.e., importance in the real world). So, what you’re asking about is a concern, but a different type of concern than what you mention. The null hypothesis using equals is just fine. The real concern is whether after rejecting the null if the effect is practically significant. February 23, 2021 at 2:40 pm Hi Jim, thank you for this explanation. I have one question. It is a probably a dumb question, but I am going to ask it anyway… Suppose I define the alpha as 5%. Does this mean that I have decided to reject the null hypothesis if p<0.05? Or when I define alpha as 5% I could use another threshold for the p-value? February 23, 2021 at 2:54 pm Hi Carolina, Yes, that’s correct! Technically, you reject the null if the p-value is less than or equal to 0.05 when you use an alpha of 0.05. So, basically what you said, but it’s less than or equal to. February 23, 2021 at 2:59 am I found this blogpost by googling for “significance false positive rate”. I noticed that what you call “false positive rate” is apparently called “false discovery rate” elsewhere. According to Wikipedia, the false positive rate is the number of false positives (FP) divided by the number of negatives (TN + FP). So FP is _not_ divided by the number of positives (TP + FP); doing this, you would get (according to Wikipedia) just the “false discovery rate”. https://en.wikipedia.org/wiki/False_positive_rate https://en.wikipedia.org/wiki/False_discovery_rate Now I fully understand that the p value is not the same as the false discovery rate, as you correctly show. But how is the p value related to the false positive rate (defined as FP/(TN + FP))? February 23, 2021 at 3:20 pm Hi Andreas, The False Discovery Rate (FDR) and the False Positive Rate (FPR) are synonymous in this context. In statistics, one concept will sometimes have several different names. For example, alpha, the significance level, and the Type I error rate all mean the same thing! As you have found, analysts from different backgrounds will sometimes use these terms differently. It does make it a bit confusing! That’s why it’s good practice to include the calculations, as I do in this post. Thanks for writing! January 12, 2021 at 10:33 am Many moons ago, when I was a junior electrical engineer, I wrote a white paper (for the US Navy). At the time, there was a big push to inject all sorts of Built-In Test (BIT) and Built-in Test Electronics (BITE) into avionics (i.e., aircraft weapon systems). The rapid pace of miniaturization of electronics made this a very attractive idea. In the paper I recommended we should slow down and inject BIT/E very judiciously, mainly for the reasons illustrated in your post. Specifically, if the actual failure rate of a weapon system is very low (i.e., the Prevalence of Real Effects is very small), and the Significance Level is too large, we will get a very high False Positive rate, which will result in the “pulling” of numerous “black boxes” for repair that don’t require maintenance. (BTW, this is what, in fact, happened. The incidence of “No Fault Found” on systems sent in for repair has gone up drastically.) And the Bayesian logic illustrated above is why certain medical diagnostic tests aren’t (or shouldn’t be) given to the general public: The prevalence in the general population is too low. The tests must be reserved for a sub-group of persons who are high risk for disease. Cheers, Joe January 12, 2021 at 3:15 pm Thanks so much for your insightful comment! These issues have real-world implications and I appreciate you sharing your experiences with us. Whenever anyone analyzes data, it’s crucial to know the underlying processes and subject area to understand correctly the implications, particularly when basing decisions on the analysis! December 9, 2020 at 9:34 am Hello Jim, I have been binge reading the blogs/articles written by you. It is very helpful. I have a question related to prevalence. Is the concept of prevalence applicable to all scenarios and end goals (for which the analysis is performed) similar to the way alpha and beta are. For example, in the example that is relate to change in per capita income (from 260 to 330), my understanding is that prevalence does not hold true, Is that correct? If not, how to interpret/understand prevalence in that example? Your inputs will be helpful. December 10, 2020 at 12:13 am In this context, the prevalence is the probability that the effect exists in the population. You’d need to be able to come up with some probability that the per capita income has changed from 260 to 330. I think coming up with a good estimate can often be difficult. It becomes easier as a track record develops. Is that size change typical or unusual in previous years? Does it fit other economic observations? Etc. Coming up with a rough estimate can help you evaluate p-values. November 23, 2020 at 8:55 am Thank you so much Jim. This was even better than what I expected when I asked you to explain: Sellke et al. I am going to suggest to all my fellow (Data) Scientists that this be a must read. November 24, 2020 at 12:25 am Thanks, Steven! I appreciate the kind words and sharing! November 23, 2020 at 8:36 am Looking forward to that. November 21, 2020 at 1:47 pm This is a nice post. The language is not just elementary, it also made complex concepts intuitively easier to grasp. I have read these concepts several times in many textbooks, for the first time I have a better understanding of the lay application behind the erstwhile difficult topics. November 21, 2020 at 12:24 am Thanks a lot Jim. It will be better, if you take this in the context of Panel data November 19, 2020 at 1:59 pm Jim, thank you. As always, so informative and you are constantly challenging me with different ways of approaching concepts. Have you or do you know of any studies that applies this approach to COVID testing? I’m thinking about recent news from Elon Musk in which he said he had 4 tests done in the same day, same test, same health professional. Two came back positive and two negative. Is there a substantial error rate on these tests? November 19, 2020 at 11:09 am Dear Sir My question is that I have a dep variable say X and a variable of interest Y with some control variables(Z) Now when I run following regressions 1) X at time t , Y & Z at t-1 2) X at time t , Y at t-1 & Z at t 3) X at time t , Y & Z at t The sign of my variable of interest changes(significance too). If there are not any theory to guide me with respect lag specification of variable of interest and control variables, which one from the above model should I use? What is the general principle November 21, 2020 at 12:08 am A good method for identify lags to include is to use the cross correlation function (CCF). This helps find lags of on time series that can predict the current value of your time series of interest. You can also use the autocorrelation function (ACF) and partial autocorrelation function (PACF) to identify lags within one time series. These functions simply look for correlations between observations of a time series that are separated by k time units. CCF is between different sets of time series data while ACF and PACF are within one set of time series data. I don’t currently have posts about these topics but they’re on my list! November 17, 2020 at 10:43 am Thanks so much for your great post. It’s always been tremendously helpful. I have one simple question about the difference between a significance level and a false positive rate. I have read your comment in one of your p-value posts: “When you’re talking significance levels and the Type I error rate, you’re talking about an entire class of studies. You can’t apply that to individual studies.” But, in this post, we simulated a test 1000 times, and in my humble opinion, it seemed like we treated 1000 tests as a kind of “a class of studies.” However, the false positive rate, 0.36, is still pretty different from the initial significance level setup, 0.05. I think this is a silly question, but could you please kindly clarify this? November 17, 2020 at 3:48 pm That’s a great question. And there’s a myriad of details details like that which are crucial to understand. That’s why it’s such a deep, dark rabbit hole! What you’re asking about gets to the heart of a major difference Frequentist and Bayesian statistics. Using Frequentist methodology, there’s no probability associated with the null hypothesis. It’s true or not true but you don’t know. The significance level is part of the Frequentist methodology. So, it can’t calculate a probability about whether the null is true. Instead, the significance level assumes the null hypothesis is true and goes from there. The significance level indicates the probability of the hypothesis producing significant results when the null is true. So, you don’t know whether the null is true or not, but you do know that IF it is true, your test is unlikely to be significant. Think of the significance level as a conditional probability based on the null being true. Compare that to the Bayesian approach, where you can have probabilities associated with the null hypothesis. The example I work through is akin to the Bayesian approach because we’re stating that the null has a 90% chance of being correct and a 10% chance of being incorrect. That’s a different scenario than Frequentist methodology where you assume the null is true. That’s why the numbers are different because they’re assessing different scenarios and assumptions. In a nutshell, yes, the 1000 tests can be a class of studies but this class includes cases where the null is both true and false at some assumed proportion. For significance levels, the class of studies contains only studies where the null hypothesis is true (e.g., 5% of all studies where the null is true). I hope that clarifies that point! November 17, 2020 at 10:32 am Idea! It is not necessary to use the notation α for the threshold (critical) value of the random variable P ̃_v=Pr[(T ̃≤-|t|│H_0 )+(T ̃≥+|t|│H_0 )] and call it the significance level. For it a different notation, for instance, p_crit should be used. There is no direct relationship between the observed p-value (p_val) and the probability of the null hypothesis P(H_0│data), just as there is no direct relationship between the critical p-value p_crit and the significance level α (the probability of a type I error)! November 17, 2020 at 3:49 pm I don’t follow your comment. Is this just your preference for the notation or something more? Alpha is the usual notation for this concept. November 17, 2020 at 3:40 am Very informative and useful. Thank you November 17, 2020 at 4:04 pm You’re very welcome! I’m glad it was helpful! Comments and Questions Cancel reply Stack Exchange Network Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. Q&A for work Connect and share knowledge within a single location that is structured and easy to search. Understanding p-values using an example Definition of p-values: A p-value is a probability that provides a measure of the evidence against the null hypothesis provided by the sample. Smaller p-values indicate more evidence against null hypothesis. Can someone please explain this in simpler terms or in a language easy to understand? I know there might already be tons of questions around understanding the interpretation of p-values, however I would ask the question in a very limited form and with the use of a specific example: A manufacturing company fills up can with mean weight of 3 pounds, the level of significance is assumed to be 0.01 H(0) : u >= 3 -- Null hypotheses H(a) : u < 3 -- Alternate hypotheses We are trying to perform a one tailed test for the case where the population standard deviation is known, so for a sample mean of 2.92 and a standard error of 0.03 , we get the z-score as -2.67 , giving us the probability (p-value) of 0.0038 or 0.38% that the sample mean would be equal to or lower than 2.92 . Since the probability of getting a sample mean equal or less than 2.92 is 0.38% , which is very small, doesn't it mean that we should accept the null hypotheses? As the chances of getting a mean of 2.92 from a sample is only 0.38%. Or am I completely missing something here? Edit - It has been three days now since I tried understanding hypothesis testing and I think I am almost there, I will try to articulate what I have understood so far and then let me know if there are still any gaps in my understanding p-values measure the likelihood of obtaining the sample mean that we obtained given that the null hypothesis is true. So for the example that I mentioned, the probability of obtaining a sample mean of 2.92 is 0.038 if that population's mean is 3 (as assumed by the null hypothesis). Now there could be two reasons for obtaining means of 2.92: The assumed population mean (i.e., the null hypothesis) is not correct, or the population mean is 3 but due to a sampling error / an unlikely sample we got a mean of 2.92. Now if we select statement 1, we run the chance of making type 1 error and this is where the level of significance comes into play. Using the level of significance we can see if we can reject the null hypothesis or cannot reject null hypothesis. hypothesis-testing statistical-significance $\begingroup$ You say the population standard deviation $\sigma$ is known. Can you provide the known value? The terminology "correction factor" is not familiar to me; can you give a formula for finding that? // The sample mean $\bar X = 2.92$ is below the hypothetical population mean $\mu_0 = 3.$ The issue is whether it is enough smaller to warrant rejecting the null hypothesis. $\endgroup$ –  BruceET Commented Apr 20, 2019 at 13:20 $\begingroup$ The population standard deviation is .18 and sample size is 36, hence the correction factor is 0.18/sqrt(36) equals 0.03 $\endgroup$ –  Rohit Saluja Commented Apr 20, 2019 at 13:24 3 $\begingroup$ Thanks for the additional information. The usual terminology is to call $\sigma/\sqrt{n}$ the 'standard error'. $\endgroup$ –  BruceET Commented Apr 20, 2019 at 13:27 $\begingroup$ @BruceET - the issue is if it is enough smaller to reject the null hypotheses, however the probability of sample mean of being less than or equal to 2.92 is only 0.0038, so can't we say that the probability of sample mean of less than 3 is very less hence we support null hypotheses. $\endgroup$ –  Rohit Saluja Commented Apr 20, 2019 at 13:39 4 Answers 4 Imagine you could measure the weight of all cans that the manufacturing company has ever made and the mean would be $2.87$ pounds. Then imagine you would take 10 cans randomly and see how much they weight. It is unlikely to get the exact mean of all cans ( $2.87$ pounds), hence you end up with a mean of $2.65$ , for example. If you would do that again and again - taking 10 cans and measuring the weight - you would get a distribution of means. The best guess about the true mean is the mean of the distribution you obtained. Extreme values like $1.9$ or $3.5$ pounds will be unlikely and even more extreme values will be even more unlikely. Doing significance tests usually means that you look how likely the mean you observed is if you assume that your sample was drawn from a population with mean zero. If the mean that you observed is very unlikely you would decide to discard the null hypothesis. The only difference between what I have said so far and your example is that you assume the null hypothesis a mean of $\ge 3$ . So the $0.38\%$ you report say that the probability of getting your mean of $2.92$ from a population with a mean of $\ge 3$ is so unlikely that you would discard the null hypothesis and accept the alternative hypothesis which is $<3$ . Your evidence indicate that the cans weight less than $3$ pounds. This means it is the opposite: having a $p$ of $0.38\%$ as you report doesn't mean you have to keep the null hypothesis because your result is so unlikely but it means that you can discard the null hypothesis because your data was very unlikely a randomly drawn sample from a population with a mean of $3$ (i.e., your data would be very unlikely given that the null hypothesis is true). $\begingroup$ Comments are not for extended discussion; this conversation has been moved to chat . $\endgroup$ –  gung - Reinstate Monica Commented Apr 23, 2019 at 14:51 Here is a figure that shows your problem on two scales: at left is the original scale in terms of pounds; at right is the standard of z-scale often used in testing. To begin, let's look at your problem in terms of the fixed significance level $\alpha = 0.01 = 1\%.$ In the right-hand panel, your $Z$ -score is shown at the heavy vertical bar at $-2.67.$ The "critical value" for a test at the 1% level is shown by the vertical dotted line at $-2.326,$ which cuts 1% of the probability from the lower tail of the standard normal distribution. Because the $Z$ -score is to the left of the critical value, one rejects the null hypothesis at level $\alpha = 1\%.$ The P-value is the probability under the standard normal curve to the left of the heavy blue line. That area is smaller than $1\%,$ so in terms of P-values, we reject $H_0$ when the P-value is smaller than $1\%.$ You can see that the left-hand plot is the same as the right-hand plot, except for scale. It is not possible to make a printed normal table for all possible normal distributions. By converting to $Z$ -scores we can always use a single printed table for the 'standard' normal distribution, which has mean 0 and standard deviation 1. If we were going to do this production-monitoring procedure repeatedly with $n = 36$ observations each time, then we could find the critical value on the 'pound' scale; it is at 2.581 pounds. (That's because $(2.581 - 3)/.18 = -2.236,$ where the $0.18$ is the standard error.) Then we could turn the testing job over to a non-statistician, with instructions: "If the average weight for 36 cans is less than 2.581 pounds, let me know because we aren't putting enough stuff in our cans." (Or if we can't even trust the non-statistician with averages, the criterion might be a total weight less than 92.92 pounds.) Since your question is actually quite precise, I would like to keep it rather concise. Definition of p-value: the p-value is the probability of the data (or even more extrem data) given the null hypothesis is actually true. If this probability is high, then there is no reason why we should reject the null hypothesis: the data is perfectly in line with the null hypothesis. If the p-value is small, then the data seems implausible given the null hypothesis. The more implausible the data, the stronger our evidence against the null. A level of significance of 0.01 means: to reject the null hypothesis, the probability of the data must be less than 1%. If the null hypothesis is actually true, we have therefore 1% chance to see data, which is so implausible that we would wrongly reject the null hypothesis. Regarding your example: there is only 0.38% chance to see this data, if the null hypothesis is true, which is below our threshold of significance. Hence, the data seems very unlikely, and therefore we conclude that we don't believe in the null hypothesis anymore. Assume the significance level is $\alpha$ , which when talking about the null hypothesis, we are usually looking at 5% or 1% and so on. In simple terms: p-value is the smallest $\alpha$ at which we reject the null hypothesis. So, when your p-value is 0.15, then we accept the null hypothesis when $\alpha$ is 5% (or our confidence interval is 90%). But change that to only have a confidence interval of 60% and you reject your null hypothesis. Similarly, when your p-value=0.0038, it means you accept the null hypothesis under any value smaller than < 0.38%. That's why you compare p-value with $\alpha$ and if p-value < $\alpha$ , you say that you cannot accept the null hypothesis. Your Answer Sign up or log in, post as a guest. Required, but never shown By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy . Not the answer you're looking for? Browse other questions tagged hypothesis-testing statistical-significance p-value or ask your own question . Featured on Meta We've made changes to our Terms of Service & Privacy Policy - July 2024 Bringing clarity to status tag usage on meta sites Hot Network Questions How soon to fire rude and chaotic PhD student? Does the overall mAh of the battery add up when batteries are parallel? how replicate this effect with geometry nodes How does a closed-cycle rocket engine keep the chamber pressure from stalling the pump turbine? Four out puzzle: Get rid of a six digit number in 4 moves What is the default font of report documentclass? How should I respond to a former student from my old institution asking for a reference? "Knocking it out of the park" sports metaphor American English vs British English? Is the Shroud of Turin about 2000 years old? MySQL 5.7: Is it relevant/risk to have external hosts in the mysql.Hosts column if "skip-networking" is enabled? Fast circular buffer Is there anything that stops the majority shareholder(s) from destroying company value? Why do combinatorists care about Kazhdan–Lusztig polynomials? Who gave God the name 'Jealous' as referred to in Exodus 34:14? SF novel where the story, or part of it, is narrated by two linked brains taking turns Reed-Solomon error count if errors cannot be corrected What sort of impact did the discovery that water could be broken down (via electrolysis) into gas have? Fitting 10 pieces of pizza in a box A binary sequence such that sum of every 10 consecutive terms is divisible by 3 is necessarily periodic? Highlight shortest path between two clickable graph vertices Why don't we observe protons deflecting in J.J. Thomson's experiment? One IO to control two LEDs. When one is lit, the other is not Can you successfully substitute pickled onions for baby onions in Coq Au Vin? Reference request: "Higher order eigentuples" as generalized eigenvectors? Recommended How physicians can fix media bias with science The assassination attempt is the straw that breaks the camel’s back. The “gaslighting” is over. The rules for truth by legacy media are never examined for objectivity. We do not have the Inquisition in the United States; we have the legacy media. One “fact-checker” measures truth by “Pinocchios.” There is a better way—hypothesis testing. Who better to know about hypothesis testing than a physician? What if the facts about how Medicare is represented by two media outlets are tested? Hypothesis testing follows four rules: 1. Identify the truth: The truth is out there. Truth-telling has nine phases, each representing a specific duty that pertains to an ideal storyteller. The initiation phase: The duty to collect all the facts. The acceptance phase: The duty to accept a fact verifiable by objective evidence. The rejection phase: The duty to reject an artifact not verifiable by objective evidence. The attribution phase: The duty to source the facts. The external review phase: The duty to examine the motives of others to influence facts. The internal review phase: The duty to examine a personal motive to influence facts. The discrimination phase: The duty to distinguish an opinion from a fact. Opinions, even a consensus by authorities, are not facts. The equanimity phase: The duty not to contaminate a fact with emotion. The analysis phase: The duty to use facts, and only facts, to arrive at a conclusion. 2. State the subject matter: It is the actual storyteller’s version of reality. The subject matter contains the same facts, but some may be subtly misrepresented, just enough to satisfy the conclusion. The subject matter is divided into the same nine phases as they pertain to the actual storyteller. 3. The Test: Each phase of the subject matter is compared to its counterpart in the truth. The comparison measures the “relative risk” resulting from the misrepresentation of a fact by the actual storyteller. If there is no difference, the relative risk equals 1.0. If there is a difference, the relative risk is greater than 1.0. A relative risk greater than 1.0 is a Risk of Bias. For the sake of transparency, the assignments of Risk of Bias are documented for anyone to see and, if need be, to dispute. A single sample of nine relative risks emerges representing each phase in the subject matter. Some are 1.0, and some are greater than 1.0. Because storytellers naturally tend to exaggerate a fact, producing a relative risk greater than 1.0, this discrepancy itself is not proof of a departure from the truth. Bias is intentional. For proof, the collective difference among the nine relative risks in all phases of the subject matter must be statistically significant. 4. Analysis: To determine a statistically significant difference, the sample is analyzed using the single-sample T-test, found in any statistical software. The level of significance, or alpha, is 0.05, which corresponds to 95 percent confidence. The population mean, or mu, is 1.0, which corresponds to the truth. The result is the p-value. If the p-value is equal to or greater than 0.05, there is no statistically significant difference between the subject matter and the truth. Although there may be a phase that contains an exaggeration, the risk of bias is not sufficient for it to misrepresent reality. Therefore, there is no bias. This is the null hypothesis. If the null hypothesis is retained, the subject matter is the null hypothesis. If the p-value is less than 0.05, there is a statistically significant difference. Therefore, there is quantifiable proof of bias. This is the alternate hypothesis. The alternate hypothesis is accepted by default. If the null hypothesis is rejected, the subject matter is the alternate hypothesis. Hypothesis testing, unlike “Pinocchios,” objectively makes a valid comparison between truth and facsimile. A Pinocchio, while quantitative, has no level of confidence. However, a p-value has a level of confidence of 95 percent. For a rational person, 95 percent confidence stands in stark contrast to a Pinocchio. As an example of hypothesis testing, the truth consists of the verifiable facts about Medicare that are publicly available in government documents. The subject matter consists of two media outlets’ versions of the truth. One storyteller is Fox News. The sample is 1.0, 1.0, 1.0, 1.0, 1.0, 1.5, 1.5, 2.0, 1.0, and the p-value is 0.051893. The collective risk of bias is not sufficient to misrepresent reality. The other storyteller is MSNBC. The sample is 1.5, 1.5, 1.5, 2.0, 1.5, 1.5, 1.5, 2.0, 2.0, and the p-value is 0.000022. The collective risk of bias is sufficient to misrepresent reality. The difference between the two p-values shows that MSNBC’s version of Medicare is 99.9 percent less reliable than Fox’s version. Howard Smith  is an obstetrics-gynecology physician. Why I won't let my wife see her EOBs anymore How compassionate communities can transform the lives of schizophrenia patients Tagged as: Mainstream media More by Howard Smith, MD The truth about medical lawsuits: What the numbers reveal The flaw with medical malpractice litigation, why most medical malpractice claims never see a courtroom, related posts. Social media: Striking a balance for physicians and parents I was trolled by another physician on social media. I am happy I did not respond. Are negative news cycles and social media injurious to our health? How I used social media to get promoted to professor Sharing mental health issues on social media How physicians can engage on social media More in physician. How a doctor transformed grief into personal growth How embracing vulnerability transforms pain into power A life of purpose: free from societal pressures that lead us astray The resilience of international medical graduates The practice of delayed gratification in medical training: a double-edged sword When a patient’s story hits close to home: a doctor’s emotional journey Most popular. A doctor’s eye-opening journey as a patient President Biden: a closer look at leadership, dignity, and aging How medical school curricula perpetuate inequality Unlock your child’s potential: the power of nurturing hidden talents The surprising secret to success in medical school Past 6 months. Struggles of navigating prestigious medical systems The truth behind opioid use disorder Creating a subspecialty track for experienced hospitalists The sham peer review: a hidden contributor to the doctor shortage The unseen dangers of faulty expert witness testimony Recent posts. From plant milk to human milk: the untapped climate solution Tax-free income with the Augusta rule [PODCAST] Subscribe to KevinMD and never miss a story! Get free updates delivered free to your inbox. Find jobs at Careers by KevinMD.com Search thousands of physician, PA, NP, and CRNA jobs now. CME Spotlights Leave a Comment Comments are moderated before they are published. Please read the comment policy . Docker is an open platform for developing, shipping, and running applications. Docker allows you to separate your applications from your infrastructure so you can deliver software quickly. With Docker, you can manage your infrastructure in the same ways you manage your applications. By taking advantage of Docker’s methodologies for shipping, testing, and deploying code quickly, you can significantly reduce the delay between writing code and running it in production. You can download and install Docker on multiple platforms. Refer to the following section and choose the best installation path for you. Docker Desktop terms Commercial use of Docker Desktop in larger enterprises (more than 250 employees OR more than $10 million USD in annual revenue) requires a paid subscription . Note If you're looking for information on how to install Docker Engine, see Docker Engine installation overview . 127 IMAGES What is P-value in hypothesis testing P-Value P-value, on the left and right tailed graphic, with null hypothesis How to Determine a p-Value When Testing a Null Hypothesis Talk Summary Using Statistics Hypothesis testing tutorial using p value method COMMENTS Understanding P-values The p value is a proportion: if your p value is 0.05, that means that 5% of the time you would see a test statistic at least as extreme as the one you found if the null hypothesis was true. Example: Test statistic and p value If the mice live equally long on either diet, then the test statistic from your t test will closely match the test ... Null Hypothesis and the P-Value. If you don't have a background in One of the most commonly used p-value is 0.05. If the calculated p-value turns out to be less than 0.05, the null hypothesis is considered to be false, or nullified (hence the name null hypothesis). And if the value is greater than 0.05, the null hypothesis is considered to be true. Let me elaborate a bit on that. Null Hypothesis: Definition, Rejecting & Examples Reject the null hypothesis when the p-value is less than or equal to your significance level. Your sample data favor the alternative hypothesis, which suggests that the effect exists in the population. ... Below are typical examples of writing a null hypothesis for various parameters and hypothesis tests. Related posts: Descriptive vs ... Understanding P-Values and Statistical Significance A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true). The level of statistical significance is often expressed as a p-value between 0 and 1. The smaller the p -value, the less likely the results occurred by random chance, and the ... S.3.2 Hypothesis Testing (P-Value Approach) Two-Tailed. In our example concerning the mean grade point average, suppose again that our random sample of n = 15 students majoring in mathematics yields a test statistic t* instead of equaling -2.5.The P-value for conducting the two-tailed test H 0: μ = 3 versus H A: μ ≠ 3 is the probability that we would observe a test statistic less than -2.5 or greater than 2.5 if the population mean ... Interpreting P values The p-value represents the strength of your sample evidence against the null. Lower p-values represent stronger evidence. Like the significance level, the p-value is stated in terms of the likelihood of your sample evidence if the null is true. For example, a p-value of 0.03 indicates that the sample effect you observe, or more extreme, had a 3 ... How to Find the P value: Process and Calculations In this case, our t-value of 2.289 produces a p value between 0.02 and 0.05 for a two-tailed test. Our results are statistically significant, and they are consistent with the calculator's more precise results. Displaying the P value in a Chart. In the example above, you saw how to calculate a p-value starting with the sample statistics. P-Value in Statistical Hypothesis Tests: What is it? The p value is the evidence against a null hypothesis. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis. P values are expressed as decimals although it may be easier to understand what they are if you convert them to a percentage. For example, a p value of 0.0254 is 2.54%. Hypothesis Testing, P Values, Confidence Intervals, and Significance The null hypothesis states that there is no statistical difference between groups based on the stated research hypothesis. ... For example, a p-value from a double-blinded randomized clinical trial (designed to minimize bias) should be weighted higher than one from a retrospective observational study . 9.3 In the first part of this example, we rejected the null hypothesis when \(\alpha = 0.05\). And, in the second part of this example, we failed to reject the null hypothesis when \(\alpha = 0.01\). There must be some level of \(\alpha\), then, in which we cross the threshold from rejecting to not rejecting the null hypothesis. p-value The p -value is used in the context of null hypothesis testing in order to quantify the statistical significance of a result, the result being the observed value of the chosen statistic . [ note 2] The lower the p -value is, the lower the probability of getting that result if the null hypothesis were true. A result is said to be statistically ... How to Write a Null Hypothesis (5 Examples) H 0 (Null Hypothesis): Population parameter =, ≤, ≥ some value. H A (Alternative Hypothesis): Population parameter <, >, ≠ some value. Note that the null hypothesis always contains the equal sign. We interpret the hypotheses as follows: Null hypothesis: The sample data provides no evidence to support some claim being made by an individual. What Is The Null Hypothesis & When To Reject It The observed value is statistically significant (p ≤ 0.05), so the null hypothesis (N0) is rejected, and the alternative hypothesis (Ha) is accepted. Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01) as general guidelines to decide if you should reject or keep the null. The p value The way to interpret that p-value is: observing 38 heads or less out of the 100 tosses could have happened in only 1% of infinitely many series of 100 fair coin tosses. The null hypothesis in this case is defined as the coin being fair, therefore having a 50% chance for heads and 50% chance for tails on each toss.. Assuming the null hypothesis is true allows the comparison of the observed data ... How to Correctly Interpret P Values In technical terms, a P value is the probability of obtaining an effect at least as extreme as the one in your sample data, assuming the truth of the null hypothesis. For example, suppose that a vaccine study produced a P value of 0.04. This P value indicates that if the vaccine had no effect, you'd obtain the observed difference or more in 4 ... The p-value and rejecting the null (for one- and two-tail tests) The p-value (or the observed level of significance) is the smallest level of significance at which you can reject the null hypothesis, assuming the null hypothesis is true. You can also think about the p-value as the total area of the region of rejection. Remember that in a one-tailed test, the regi How To Calculate P-Value in 3 Steps (With an Example) How to calculate p-value. Below are steps you can use to help calculate the p-value for a data sample: 1. State the null and alternative hypotheses. The first step to calculating the p-value of a sample is to look at your data and create a null and alternative hypothesis. For example, you could state that a hypothesized mean "μ" is equal to 10 ... P-Value & Hypothesis Testing: Examples This probability is called the P-value. If the value of p-value is smaller than the level of significance, it provides evidence against the null hypothesis. For example, let's say we are testing the claim that the students studying more than 6 hours on average get more than 75% marks. Here are the steps followed: P-Value (Definition, Formula, Table & Example) This example shows that the p-value is entirely dependent on the test statistic used and that p-values can only be used to reject a null hypothesis, not to explore an alternate hypothesis. P-value Formula. We Know that P-value is a statistical measure, that helps to determine whether the hypothesis is correct or not. P-value is a number that ... P-value Formula Therefore, the null hypothesis is accepted. Example 2: P-value is 0.3105. If the level of significance is 5%, find if we can reject the null hypothesis. Solution: Looking at the P-value table, the p-value of 0.3105 is greater than the level of significance of 0.05 (5%), we fail to reject the null hypothesis. Example 3: P-value is 0.0219. P-Values, Error Rates, and False Positives The precise value of the p-value affects the size of that decrease. Smaller p-values cause a larger decline. Finally, the posterior probability is also the false positive rate in this context because of the following: the low p-values cause the hypothesis test to reject the null. Understanding the Null Hypothesis for ANOVA Models To decide if we should reject or fail to reject each null hypothesis, we must refer to the p-values in the output of the two-way ANOVA table. The following examples show how to decide to reject or fail to reject the null hypothesis in both a one-way ANOVA and two-way ANOVA. Example 1: One-Way ANOVA hypothesis testing p-values measure the likelihood of obtaining the sample mean that we obtained given that the null hypothesis is true. So for the example that I mentioned, the probability of obtaining a sample mean of 2.92 is 0.038 if that population's mean is 3 (as assumed by the null hypothesis). Now there could be two reasons for obtaining means of 2.92: The ... 10 Statistics Questions to Ace Your Data Science Interview Answer: Given that the null hypothesis is true, a p-value is the probability that you would see a result at least as extreme as the one observed. P-values are typically calculated to determine whether the result of a statistical test is significant. In simple words, the p-value tells us whether there is enough evidence to reject the null ... How physicians can fix media bias with science Therefore, there is no bias. This is the null hypothesis. If the null hypothesis is retained, the subject matter is the null hypothesis. If the p-value is less than 0.05, there is a statistically significant difference. Therefore, there is quantifiable proof of bias. This is the alternate hypothesis. The alternate hypothesis is accepted by default. Get Docker Download and install Docker on the platform of your choice, including Mac, Linux, or Windows. assignment essay homework paper phd report resume review speech